密砂单剪试验的非共轴本构数值分析

罗 强, 郑伟花

(1.南阳师范学院 土木建筑工程学院，河南 南阳 473061; 2.大连理工大学 土木工程学院岩土工程研究所，辽宁 大连 116024)

密砂单剪试验的非共轴本构数值分析

罗 强1, 2, 郑伟花1

(1.南阳师范学院 土木建筑工程学院，河南 南阳 473061; 2.大连理工大学 土木工程学院岩土工程研究所，辽宁 大连 116024)

在土体主应力方向的旋转过程中，主应力方向与塑性主应变增量方向之间存在非共轴现象，传统的共轴本构理论无法合理描述非共轴现象及其对应力-应变关系的影响。通过有限元二次开发，在应变软化共轴模型的基础上引入了角点结构非共轴理论，对密砂的单剪试验进行数值模拟及分析，系统地研究了非共轴现象及其影响。数值分析结果与试验结果的对比表明：非共轴模型能够合理地反映非共轴现象及其影响，且非共轴现象受到静止侧压力系数、竖向应力和流动法则等因素的显著影响。

非共轴；本构理论；应变软化；单剪试验；数值分析

1 研究背景

传统的岩土材料本构模型建立在共轴理论上，即主应力方向与塑性主应变增量方向是完全重合的。许多研究表明[1-3]这种理论只适用于各向同性材料，而岩土材料通常是各向异性的，传统理论并不能准确地反应颗粒材料的应力应变状态。事实上，在土体主应力方向的旋转过程中，主应力方向与塑性主应变增量方向之间并不是完全重合的，即存在非共轴现象，该现象在许多试验中已被观测到[4-8]。

国内外研究学者相继提出和完善了许多颗粒状材料的非共轴理论，且一些非共轴理论已经被应用到复杂岩土工程问题的数值计算中。Bardet[9]在双轴加载条件下研究了非共轴现象对砂土剪切带角度的影响。Papamichos和Vardoulakis[10]在应变硬化模型的基础上引入了非共轴理论，并对砂土剪切带的角度、形成机理和围压的影响进行了研究。Hashiguchi和Tsutsumi[11]采用非共轴模型研究了不排水双轴压缩试验中剪切带的发展情况。扈萍、黄茂松等[12]在弹塑性本构模型中引入非共轴塑性流动理论来描述非共轴现象，其研究结果表明非共轴理论的引入使得模型能够合理预测主应力方向和主应变增量方向的变化规律。黄茂松等[13]将传统的弹塑性本构模型三维化，引入三维非共轴塑性流动理论，建立了粗粒土的非共轴本构模型，对粗粒土的单剪试验进行了数值模拟。Yang和Yu[14]将角点结构非共轴理论运用到有限元数值计算中，对砂土单剪试验进行了数值模拟，并研究了非共轴现象对试样的应力-应变关系的影响。Yang和Yu[15]将角点结构非共轴理论应用到临界状态弹塑性模型[16-17]中，研究了非共轴现象对Erksak砂和Weald黏土在主应力方向旋转时的力学特性的影响。

关于非共轴现象的本构模型是当前土力学研究中的热点问题之一，然而，目前的研究工作大多是在理想弹塑性或应变硬化本构模型中开展的，很少在密砂的应变软化本构模型中对非共轴现象及其影响进行研究，也较少针对非共轴现象的影响因素进行系统地研究。本文在应变软化本构模型的基础上引入了角点结构非共轴理论，对密砂试样的单剪试验进行了有限元模拟，研究了主应力方向旋转、非共轴现象、以及非共轴现象对试样的应力-应变关系的影响。另外，探讨了流动法则、静止侧压力系数、竖向压力等因素对非共轴现象的影响。

2 非共轴本构模型的建立

图1 非共轴、传统塑性应 变增量在屈服面上的关系

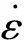
根据角点结构非共轴弹塑性理论可知：

(1)

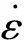
密砂的应力-应变关系具有显著的应变软化特点，而且往往不具备单值函数关系，因此，反映应变软化特性的数学模型一般具有比较复杂的形式。针对密实砂的应力-应变关系特性，Rokonuzzaman和Toshinori[19]提出了一种便于数值应用的应变软化模型，该模型的屈服函数(f)和塑性势函数(g)分别采用Mohr-Coulomb函数和Drucker-Prager函数的形式，如下所示:

(2)

(3)

(4)

公式(3)中的洛德角θ表示为

(5)

其中q和J3采用式(6)和式(7)的表述形式,即：

(6)

(7)

式(2)中的函数μ(ξp)如式(8)所示，即

(8)

其中函数μp和μr分别采用式(9)和式(10)的表述形式,即：

(9)

(10)

机动摩擦角øm采用式(11)的表述形式，即

(11)

式(4)中的函数α(ξp)如式(12)所示，即

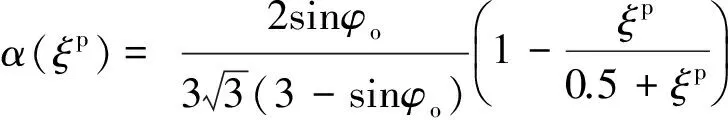
(12)

膨胀角φm采用如式(13)表述形式，即

sinφm=α(ξp) 。

(13)式中：q为广义剪应力；J3为偏应力张量第三不变量；sij为偏应力张量；øult为内摩擦角的峰值；ør为内摩擦角的残余强度；φo为膨胀角的峰值。

塑性硬化模量Kp的表达形式如下所示:

(14)

其中μ(ξp)如式(8)所示。

应变软化模型的弹性模量如下所示：

(15)

(16)

(17)

式中:e0为材料的初始孔隙比；v为泊松比；常数项G0为初始模量；Pa=98 kPa为大气压力。

(18)

(19)

其中，hnc为非共轴塑性模量，它为累积塑性应变ξp的函数，即

(20)

式中:hnco为初始非共轴塑性模量；b1，b2为模型系数，其值分别为-16和0.7。

式(19)可以重新表达为

(21)

(22)

将式(1)、式(18)、式(21)和式(22)结合在一起，得到非共轴弹塑性本构模型的表达形式为

(23)

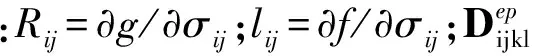
基于有限元软件ABAQUS的二次开发端口UMAT，采用显式积分算法和自动分步法，对上述应变软化非共轴本构模型进行数值积分，具体思路见罗强等人的文献[20]。

3 密砂单剪试验的数值模拟及分析

3.1 单剪试验简介

在单剪试验中，如图2所示，方形试样被放置于标准剪切容器中，试样的荷载和边界条件比较简单明确，许多研究学者通过该试验研究主应力方向的旋转，且该试验比较便于数值模拟的实施。

图2 单剪试验工作原理

基于大量的单剪试验结论，Roscoe[5]认为试样中间1/3部分(图2中jkmn区域)内的应力分布比较均匀，可将该区域作为整个试样的代表。

3.2 单剪试验的数值模拟

有限元模型采用单一的四边形平面应变单元，其类型为8节点二次缩减积分单元。在模型顶边施加水平位移边界条件，模型的左右两边保持直线状态；模型底边的竖向和水平方向位移均被固定；竖向应力σyy施加在模型的顶面，并保持不变。

在单剪过程中，由于剪应力τxy的作用，模型沿水平方向将会产生应力变化Δσxx，以及竖直方向的应变εyy。由于试样的受力情况考虑为平面应变情况，并且对模型左右两边始终保持直径状态，因此，整个模型中的应力σxx与σzz是相等的。模型主应力方向的旋转是由剪应力的τxy变化引起的。有限元模型及变形形状如图3所示。

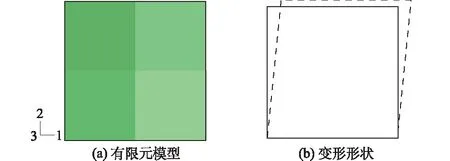
图3 单剪试验有限元模型及变形形状

主应力方向和塑性主应变增量方向的旋转如图4所示，虚线为变形后的状态，实线为初始状态，α为主应力或塑性主应变增量方向的旋转角度。

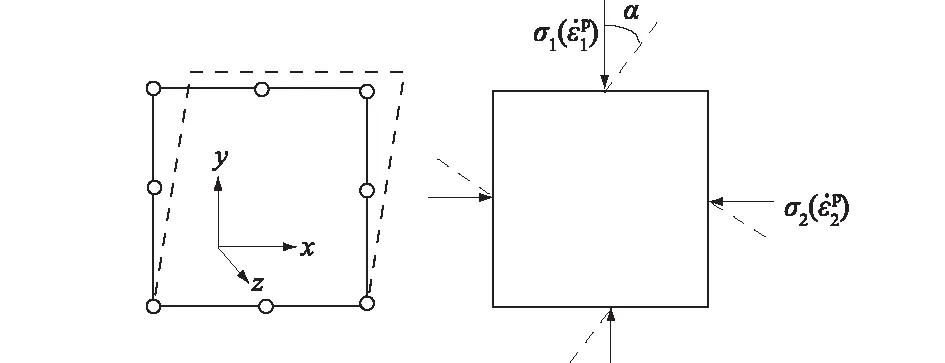
图4 主应力方向和塑性主应变增量方向的旋转

在数值计算过程中，本构模型的流动法则主要分为3种情况：相关联流动法则、非关联流动法则和塑性体积应变为0。静止侧压力系数K0采用0.2和0.5。竖向应力σyy采用135, 270，405 kPa。

3.3 数值计算结果分析

3.3.1 剪应力比-剪应变关系

当竖向应力σyy=135 kPa时，在流动法则的3种情况下，采用不同的静止侧压力系数，由共轴和非共轴模型计算所得到的剪应力比-剪应变关系曲线如图5所示。图中竖向坐标为剪应力与竖向应力之比，即τxy/σyy。非共轴模型中的hnco/G分别取为0.2，0.4，0.8。

图5 σyy=135 kPa时数值计算结果

由图5可以发现：

(1) 在剪切变形的初期，共轴与非共轴模型的计算结果比较接近；随着剪切变形的发展，非共轴模型计算得到的剪应力比的增长速度滞后于共轴模型计算结果的增加速度，并且，两者之间的差异逐渐显著；当剪应力比达到峰值时，2种模型的计算结果之间的差异达到最大；当试样抗剪强度由峰值向残余强度发展时，剪应力比随着剪应变的增长而减小，2种模型的计算结果之间的差异逐渐减小；当试样的抗剪强度达到临界状态以后，2种模型的计算结果完全一致。

(2) 当流动法则相同时，随着静止侧压力系数的增加，共轴和非共轴模型计算结果之间的差异产生时所对应的剪应力比逐渐增加。例如：在图5(a)和图5(b)中，静止侧压力系数分别为0.2和0.5，非共轴和共轴模型计算结果之间的差异分别在剪应力比达到0.3和0.6时开始出现，然而，这种差异均在剪应变为0.15时消失。

(3) 非共轴模型计算得到的剪应力比的增长趋势滞后于共轴模型计算结果的增长趋势，该现象随着hnco/G的减小而越来越明显。

(4) 在关联和非关联流动法则的计算结果中，应力-应变关系的应变软化特性比较明显，随着hnco/G的减小，剪应力比峰值逐渐减小。在塑性体积应变为0时的计算结果中，应变软化特性不明显，2种模型计算得到的剪应力比峰值比较接近。

当作用在试样的竖向应力σyy为270 kPa和405 kPa时，由共轴和非共轴模型对单剪试验进行了数值模拟，相关计算结果表明：①当流动法则和静止侧压力系数相同时，随着竖向应力的增加，非共轴与共轴模型计算结果之间的差异越来越显著；②在相同的静止侧压力系数和竖向应力条件下，当流动法则由关联法则变化到塑性体积应变为0时，应力-应变关系的应变软化特性逐渐减弱，非共轴与共轴模型计算结果之间的差异逐渐减小；③当流动法则和竖向应力相同时，随着静止侧压力系数的增加，共轴模型和非共轴模型计算结果之间的差异逐渐减小。

3.3.2 主应力方向与塑性主应变增量方向的旋转

当σyy=135 kPa，K0=0.2时，共轴模型计算所得到的主应力方向和塑性主应变增量方向的旋转变化，如图6所示。

图6 K0=0.2共轴模型计算结果

由图6可以发现：

(1) 主应力方向和塑性主应变增量方向的旋转变化是完全重合的。

(2) 在相同的静止侧压力系数和竖向应力条件下，当流动法则由关联流动法则变化至塑性体积应变为0时，主应力方向的极值逐渐减小。例如：在图6中，关联流动法则所得到的主应力方向极值为67°，非关联流动法则的结果为55°，塑性体积应变为0时的结果为45°。

(3) 当流动法则和竖向应力相同时，静止侧压力系数对主应力方向的极值没有影响，但是，对其旋转范围具有影响。例如：在图6(a)中，当K0=0.2时，主应力方向的旋转范围为0°～67°。可见，随着静止侧压力系数的增加，主应力方向的旋转范围逐渐减小。

3.3.3 非共轴现象分析

当hnco/G=0.2，σyy=135 kPa，K0=0.2时，非共轴模型计算得到的主应力方向和塑性主应变增量方向的旋转变化，如图7所示。

图7 K0=0.2非共轴模型计算结果

由图7可以发现：

(1) 非共轴模型能够反映主应力方向和塑性主应变增量方向之间的非共轴现象。

(2) 当剪切变形较小时，主应力方向的增长趋势滞后于塑性主应变增量方向的增长趋势，且前者的旋转范围要低于后者的范围；随着剪切变形的增加，主应力方向的增长趋势领先于塑性主应变增量方向的增长趋势，且前者的旋转范围高于后者的范围；在剪切变形的后期，塑性主应变增量方向与主应力方向逐渐重合，非共轴现象逐渐消失。

(3) 在相同的静止侧压力系数和竖向应力条件下，当流动法则由关联流动法则变化至塑性体积应变为0时，非共轴现象逐渐减弱。

(4) 以关联流动法则的计算结果为例，在图7(a)中，当K0=0.2时，主应力方向的旋转范围为0°～67°，塑性主应变增量方向的旋转范围为25°～67°。可见，当流动法则和竖向应力相同时，随着静止侧压力系数的增加，主应力方向与塑性主应变增量方向的旋转范围之间的差异逐渐减小，非共轴现象逐渐减弱。

3.4 数值计算结果与试验结果的对比

在竖向应力σyy=135 kPa的条件下，Roscoe[5]所进行的密砂单剪试验的结果，如图8所示。

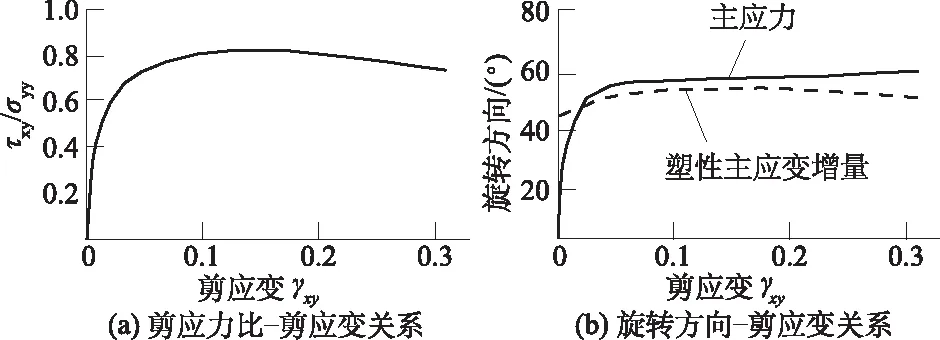
图8 单剪试验结果

将图5、图7与图8进行对比，可以发现：①试验和数值计算所得到的应力-应变关系都具有显著的应变软化特点。②在试验结果中，非共轴现象在剪切变形初期比较显著，这与数值计算结论是相一致的。在剪切变形的后期，主应力方向和塑性主应变增量方向都达到了极值，前者的数值略大于后者，这是由于试验误差所引起的；如果能够消除试验误差等因素的影响，两者应当是重合的[4]，而这种试验误差的影响在数值计算结果中则不存在。③当选取比较合理的hnco/G时，非共轴模型的计算结果与试验结果比较接近。

4 结 论

传统的共轴本构理论无法描述主应力方向旋转过程中的非共轴现象。通过有限元二次开发，在应变软化共轴模型的基础上引入了角点结构非共轴理论，针对密砂的单剪试验进行数值模拟及分析，主要得到以下结论：

(1) 数值计算结果与试验结果比较接近，表明非共轴模型能够合理地反映非共轴现象及其对应力-应变关系的影响。

(2) 当剪切变形较小时，主应力方向的增长趋势滞后于塑性主应变增量方向的增长趋势；随着剪切变形的发展，主应力方向的增长趋势领先于塑性主应变增量方向的增长趋势；在剪切变形的后期，两者逐渐趋于一致，非共轴现象消失。

(3) 非共轴模型计算得到的剪应力比增长趋势要滞后于共轴模型计算结果的增长趋势。非共轴模型所得到的剪应力比峰值要低于共轴模型的计算结果；当试样的抗剪强度达到残余强度时，非共轴模型与共轴模型的计算结果之间没有差异。

(4) 静止侧压力系数、竖向应力和流动法则等因素对非共轴现象具有显著的影响。

[1] MADSEN O S. Wave-induced Pore Pressures and Effective Stresses in a Porous Bed[J]. Geotechnique, 1978, 28(4): 377-393.

[2] ISHIHARA K, TOWHATA I. Sand Response to Cyclic Rotation of Principal Stress Directions as Induced by Wave Loads[J]. Soils and Foundations, 1983, 23(4): 11-26.

[3] YAMAMOTO T, KONING H L, SPELLMEIGHER H. On the Response of a Poro-elastic Bed to Water Waves[J]. Journal of Fluid Mechanics, 1978, 87(1): 193-206.

[4] ROSCOE K H, BASSETT R H, COLE E R. Principal Axes Observed During Simple Shear of a Sand[C]∥Proceedings of the Geotechnical Conference Oslo 1967 on Shear Strength Properties of Natural Soils and Rocks, Oslo : Norwegian Geotechnical Institute, 1967: 231-237.

[5] ROSCOE K H. The Influence of Strains in Soil Mechanics[J]. Geotechnique, 1970, 20(2):129-170.

[6] ODA M, KONISHI J. Microscopic Deformation Mechanism of Granular Material in Simple Shear[J]. Soils and Foundations, 1974, 14(4):25-38.

[7] DRESCHER A, DE JOSSELIN DE JONG G. Photoelastic Verification of a Mechanical Model for the Flow of a Granular Material[J]. Journal of Mechanics and Physics of Solids, 1972, 20(5):337-351.

[8] ISHIHARA K, TOWHATA I. Sand Response to Cyclic Rotation of Principal Stress Direction as Induced by Wave Loads[J]. Soils and Foundations, 1983, 23(1):11-16.

[9] BARDET J P. Orientation of Shear Bands in Frictional Soils[J]. Journal of Engineering Mechanics, 1991, 117(7):1466-1484.

[10] PAPAMICHOS E, VARDOULAKIS I. Shear Band Formation in Sand According to Non-coaxial Plasticity Model[J]. Geotechnique, 1995, 45(5):649-661.

[11] HASHIGUCHI K, TSUTSUMI S. Shear Band Formation Analysis in Soils by the Subloading Surface Model with Tangential Stress Rate Effect[J]. International Journal of Plasticity, 2003, 19(10):1651-1677.

[12] 扈 萍, 黄茂松, 钱建固, 等. 砂土非共轴特性的本构模拟[J]. 岩土工程学报, 2009, 31(5):793-798. (HU Ping, HUANG Mao-song, QIAN Jian-gu,etal. Non-coaxial Plasticity Constitutive Modeling of Sands[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(5):793-798. (in Chinese))

[13] 黄茂松, 孙海忠, 钱建固. 粗粒土的非共轴性及其离散元数值模拟[J]. 水利学报, 2010, 41(2):172-181. (HUANG Mao-song, SUN Hai-zhong, QIAN Jian-gu. Non-coaxial Behavior of Coarse Granular Aggregates Simulated by DEM[J]. Shuili Xuebao, 2010, 41(2):172-181. (in Chinese))

[14] YANG Yun-min, YU H S. Numerical Simulations of Simple Shear with Non-coaxial Models[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(1):1-19.

[15] YANG Yun-min, YU H S. A Non-coaxial Critical State Soil Model and Its Application to Simple Shear Simulations[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(13): 1369-1390.

[16] YU H S. CASM: A Unified State Parameter Model for Clay and Sand[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1998, 22(8):621-653.

[17] YU H S, KHONG C D, WANG J,etal. Experimental Evaluation and Extension of a Simple Critical State Model for Sand[J]. Granular Matter, 2005, 7(4):213-225.

[18] RUDNICKI J W, RICE J R. Conditions for the Localisation of Deformation in Pressure-sensitive Dilatant Materials[J]. Journal of Mechanics and Physics of Solids, 1975, 23(6):371-394.

[19] MD ROKONUZZAMAN, TOSHINORI S. Model Tests and 3D Finite Element Simulations of Uplift Resistance of Shallow Rectangular Anchor Foundations[J]. International Journal of Geomechanics, 2012, 12(2):1-24.

[20] 罗 强, 王忠涛, 栾茂田, 等. 非共轴本构模型在地基承载力数值计算中若干影响因素的探讨[J]. 岩土力学, 2011, 32(增1):732-737. (LUO Qiang, WANG Zhong-tao, LUAN Mao-tian,etal. Factors Analysis of Non-coaxial Constitutive Model’s Application to Numerical Analysis of Foundation Bearing Capacity[J]. Rock and Soil Mechanics, 2011, 32(Sup.1):732-737. (in Chinese))

(编辑：陈 敏)

Numerical Analysis of Simple Shear Test onDense Sand with Non-coaxial Constitutive Model

LUO Qiang1, 2, ZHENG Wei-hua1

(1.School of Civil Engineering and Architecture, Nanyang Normal University, Nanyang 473061, China; 2.Institute of Geotechnical Engineering, School of Civil Engineering, Dalian University of Technology, Dalian 116024, China)

In the process of rotation of the orientation of principal stress, the non-coaxial phenomenon exists between the orientations of the principal stress and plastic strain rate. However, the traditional constitutive theory could not reflect the non-coaxial phenomenon and its influence on the relationship between stress and strain. The yield vertex non-coaxial theory is adopted into a strain softening coaxial model to research the non-coaxial phenomenon and its influence in the numerical simulations of simple shear test on dense sand. Comparison between numerical result and test result suggests that the non-coaxial model could reflect the non-coaxial phenomenon and its influence reasonably, and also, the roles of non-coaxial model are considerably influenced by static lateral pressure coefficients, vertical stress and flow rules.

non-coaxial; constitutive theory; strain softening; simple shear test; numerical analysis

2013-12-12；

2014-01-05

国家自然科学基金项目(51079018, 11202109)；河南省科技攻关重点项目(112102310499)；河南省教育厅科学技术研究重点项目(14B560023)

罗 强(1981-), 男, 河南南阳人, 讲师,博士, 主要从事岩土本构理论的数值应用和离心模型实验方面的研究, (电话)15938448276(电子信箱)luoqiang1212@sina.com。

10.3969/j.issn.1001-5485.2015.05.017

2015,32(05):89-94

TU441

A

1001-5485(2015)05-0089-06