基于尖点突变理论的非均质土坡失稳判据分析

史俊涛，孔思丽，贺 俊，黄春晖

(1.天门市建筑业管理处，湖北 天门 431700；2.贵州大学 土木工程学院，贵阳 550025；3.西南石油大学 土木工程与建筑学院，成都 610500)

基于尖点突变理论的非均质土坡失稳判据分析

史俊涛1,2，孔思丽2，贺 俊3，黄春晖2

(1.天门市建筑业管理处，湖北 天门 431700；2.贵州大学 土木工程学院，贵阳 550025；3.西南石油大学 土木工程与建筑学院，成都 610500)

为避免失稳判据的主观人为性，将非线性突变理论运用于非均质边坡稳定性评价中。结合工程算例建立非均质土坡数值计算的力学模型，采用强度折减有限元法对土坡进行稳定性分析，通过建立坡体内部水平方向最大位移与强度折减系数的尖点突变模型，将失稳判据量化为一个确定的突变特征值，比较各级强度下的水平最大位移突变特征值与0的关系确定土坡稳定安全系数，并将所得结果与塑性区贯通判据、计算不收敛判据及Spencer法计算结果进行对比分析。结果表明：以尖点突变模型为失稳判据能确定出土坡稳定形态与强度折减系数的定量关系，展现土坡失稳过程的突变性，其物理意义明确，计算结果客观，求解出的安全系数精度较高。该失稳判据为非均质土坡稳定性分析的较优判据。

非均质边坡；尖点突变理论；稳定性分析；失稳判据；D-P系列准则；强度折减法

1 研究背景

边坡稳定性分析是岩土工程领域一个基本而重要的研究课题，也是边坡进行支护设计的前提条件。近些年来，随着计算机技术高速发展和数值分析理论的不断完善，将强度折减法与有限元法结合应用于边坡稳定分析中逐渐成为新趋势，受到众多研究者的青睐。此法不仅能够模拟复杂的边界条件和几何条件，展现坡体内部各个单元及节点处的应力、应变、位移等信息，而且可以通过岩土体强度参数的折减来定量求出边坡整体稳定安全系数和潜在滑移面，克服了传统极限平衡法需事先假定滑移面形状和位置的弊端，具有更强的实用性。

强度折减法分析边坡稳定性问题的关键在于如何准确判定边坡是否处于临界失稳状态。目前边坡失稳判据主要有3种：①数值计算不收敛[1]；②坡体特征部位位移突变[2]；③塑性应变从坡脚到坡顶形成贯通的滑移面[3-4]。考虑到边坡稳定性问题本质上是不可逆的变形演化过程，其失稳可以看作坡体位移从连续逐渐变化到突变的过程，因此，将坡体关键点位移随强度折减系数的变化关系曲线作为失稳判定标准具有较为明确的物理意义。由于突变理论注重研究系统中考察量为何从连续逐渐变化导致系统状态的突然变化[5]，一些研究者将其引入岩土体结构稳定性分析中。付成华等[6]将突变理论运用到地下工程洞室围岩稳定分析上，根据系统突变条件从不同方面判别洞室围岩发生失稳的可能性；郑东健等[7]基于突变理论研究了高拱坝的整体稳定性，指出了塑性总应变能失稳判据的优越性；李凯等[8]将突变理论应用于均质边坡的稳定性分析中，验证了此法的可行性。鉴于此，本文结合实际工程采用数值分析方法模拟非均质土坡在不同强度条件下向临界失稳状态演化的全过程，依据突变理论对坡体水平方向最大位移与强度折减系数的关系曲线进行多项式拟合，建立坡体水平方向最大位移与强度折减系数的尖点突变模型，并以此作为非均质土坡临界失稳的判定标准，消除主观人为因素的影响，进而实现失稳判据的量化，为非均质土坡的稳定性评价提供了一个新的定量研究方法。

2 非均质边坡中D-P系列准则间参数换算

Drucker-Prager(简称D-P)准则中α，k的取值不同代表着不同的屈服准则，采用不同的屈服准则得出不同的安全系数。由于ABAQUS等有限元分析软件多内置DP1 (外角点外接圆)准则，因此要求解其他D-P准则条件下的安全系数就要实现不同D-P准则间的参数转换。不同D-P屈服准则在主应力空间的屈服面是一系列圆锥面，在π平面上为同心圆系，其在偏平面上半径r的表达式为[9]

(1)

式中：J2为应力偏张量的第二不变量；I1为应力张量的第一不变量；α，k是岩土体强度参数c，ø的函数。

若通过一定的变换使D-P系列准则在应力空间上的半径相等，便可实现不同D-P准则间的等价转换。观察式(1)可知，在既定的应力条件下，I1为不变量，半径r只与k，α有关，可以通过调整α，k来实现非均质边坡中D-P系列准则间的等价转换。文献[10]认为在平面应变条件下，DP5(摩尔-库伦匹配D-P)准则与Mohr-Coulomb准则等效。鉴于此，以DP1和 DP5准则为例，设c1，ø1为岩土体的实际强度指标，若使用DP5准则求解安全系数，其参数α5，k5表示为：

(2)

而DP1准则的参数α1，k1表示为：

(3)

联立式(2)和式(3)，并令α1=α5，k1=k5可求解得到：

(4)

(5)

这时在DP1准则条件下采用参数c5，ø5进行计算与使用参数c1，ø1在DP5准则中进行计算具有等价性。进而可知，在自带DP1准则的有限元分析软件中，基于DP1准则采用c5，ø5就能实现DP5准则(计算参数为c1,ø1)的有限元数值计算。对于非均质土坡而言，如果采用DP5准则计算稳定安全系数，可先根据式(4)和式(5)对各土层的强度参数进行换算，并将换算后的参数代入有限元分析软件中进行数值计算，即可实现使用DP5准则对具有多层土体的非均质边坡的稳定性计算。依据上述方法调整岩土强度参数c，ø，便可实现其他D-P准则与DP1准则之间的等价变换。

3 失稳突变模型

非均质边坡变形失稳的过程中伴随着坡体相应部位位移发生无限制的塑性流动，因此，在采用强度折减法进行非均质边坡稳定性分析时，以坡体水平位移为考察量，通过建立其与强度折减系数的突变模型函数S(F)来考察非均质土坡整体安全稳定性。

随着土体强度逐级折减可得到不同折减系数下的水平方向位移场，将各级强度下的水平位移值S与强度折减系数F的函数关系式进行Taylor级数展开，截取至5次方展开为

S(F)=c0+c1F+c2F2+c3F3+c4F4+c5F5。

(6)

式中：c0，c1，c2，c3，c4，c5均为待定系数。

对式(6)两边求取导数得到势函数后，消除势函数中的3次方系数项，将其化为尖点突变模型的标准形式，令F=n-m，m=c4/(5c5)则有：

V=d0+d1n+d2n2+d4n4。

(7)

其中，d0，d1，d2，d4分别为：

(8)

(9)

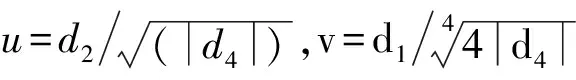
由式(9)两边对ρ求取导数，并令其导函数等于0，则可以得到正则和对偶突变的平衡曲面方程为

(10)

式(10)决定的临界点集为平衡曲面如图1所示，该曲面在(ρ，u，v)三维空间上由上、中、下3叶组成，其中上、下2叶稳定，中叶不稳定。当相点(ρ，u，v)到达上、下叶的边缘时会发生突跳而越过中叶，因此，在平衡曲面上有竖直切线的点组成状态的突变点集[6](即为奇点集)，方程式为

(11)

联合式(10)和式(11)消去ρ进行求解，可得突变特征值方程为

(12)

图1 2种尖点突变模型的平衡曲面

采用强度折减法分析非均质土坡的稳定性，基于突变理论判定非均质边坡的状态为：当Δ>0时，坡体水平位移稳定，表明土坡处于稳定状态；当Δ≤0时，坡体水平位移不稳定，意味着土坡发生失稳破坏。

4 基于突变理论的非均质边坡稳定性强度折减法的分析过程

4.1 强度折减法理论

强度折减法基本原理[11]是将岩土体强度参数值c，tanø采用同时除以一个折减系数F，得到一组新的c′,tanø′值，并以新的参数值代入进行反复试算，直至边坡处于临界失稳状态，其分析方程式如下：

(13)

(14)

4.2 基于尖点突变模型的非均质边坡稳定性强度折减法计算

计算流程如图2所示。

图2 计算流程

5 工程应用

5.1 非均质边坡几何尺寸及力学参数

某非均质土坡由3层不同类型的土体组成，其边坡几何尺寸如图3所示，计算边界条件为：坡底水

图3 非均质土坡几何尺寸和材料分区

平和竖向位移均固定，左右两侧约束水平方向位移，其他部位为自由边界，各层土体的物理力学参数见表1。

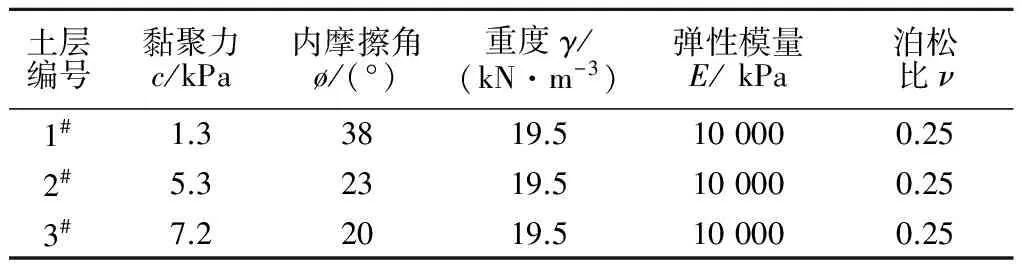
表1 非均质土坡物理力学参数

基于平面应变建立土坡数值计算模型，对于土体采用弹塑性本构关系及服从DP5屈服准则和非关联流动法则。采用PLANE2单元进行网格划分，计算模型共划分5 848个单元，11 925个节点。对于非线性计算采用大变形静态分析，全牛顿-拉普森迭代法，最大的迭代次数为1 000次，并使用稀疏矩阵求解器进行求解，以不平衡力和位移作为误差收敛条件，收敛容许值设定为0.000 1，重力荷载一次性施加，最大荷载子步设定为100步，打开自适应下降因子及自动收索选项。

5.2 不同失稳判据所得结果比较分析

5.2.1 数值计算不收敛

采用强度折减法有限元进行土坡稳定性分析时，先通过式(4)和式(5)换算出与DP5准则相应的各层土体的初始强度计算参数(见表2)，以F=1.1开始对各层土体在DP5条件下的初始强度参数进行折减，当F=1.46时，数值计算收敛;当F=1.47时，计算所得到的土坡已经发生较大的变形，其位移严重失真，网格单元变形已超出土坡的自身构型，因此，以数值计算不收敛为失稳判据计算出的土坡整体稳定安全系数为1.46。

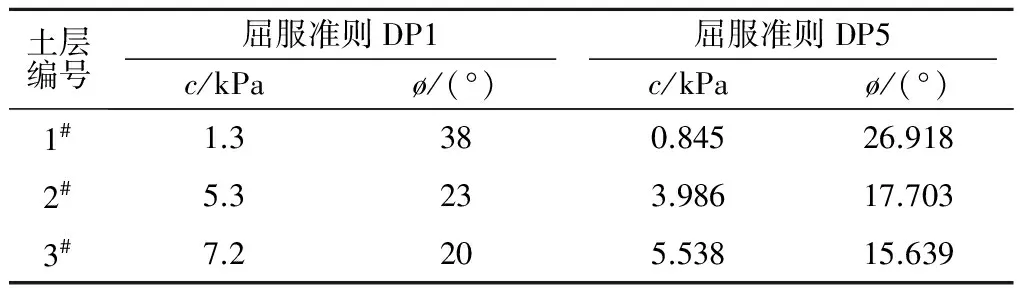
表2 各层土体在DP5准则下的初始计算参数

5.2.2 塑性区贯通

非均质土坡的失稳破坏可以看作是等效塑性区逐渐开展、扩大直至贯通而进入完全塑性流动状态，继而无法承受荷载的过程。通过数值有限元计算，得出不同强度折减系数下的等效塑性应变云图(见图4)。

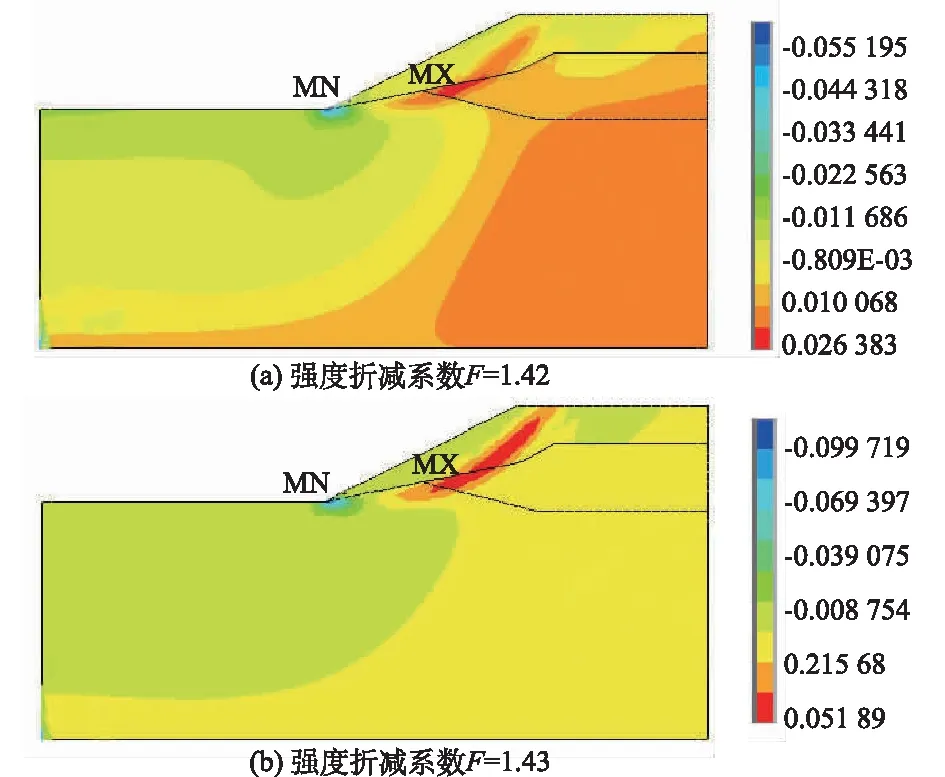
图4 不同强度折减系数下的塑性应变云图

从图4中可以看出，随着强度折减系数的增大，剪切塑性应变从坡脚向坡顶上缘延伸。对比图4中塑性应变的分布，由于土坡的分层导致土层的分界面上部分塑性区分布不连续，当F为1.42时坡体塑性区尚未贯通，当F达到1.43时坡体内部塑性区恰好贯通，因此，以塑性区贯通作为失稳判据求得的安全系数为1.42。

5.2.3 尖点突变模型失稳判据

由于非均质土坡变形场较为复杂，坡体不同部位的位移场与折减系数的变化关系是非唯一的，选择不同的位移参考点会对计算精度产生一定影响，而坡体内水平方向最大位移是确定的。为此，本文选取坡体水平方向最大位移作为分析标准，依据突变理论建立尖点突变模型失稳判据，可以减少主观人为的不确定性，实现计算结果的量化和确定化。

以Fk=1.1开始对各土层在DP5条件下的初始计算参数进行折减，计算各级强度下边坡的水平位移场，得出坡体最大水平位移随强度折减系数的演化规律如图5所示。当折减系数为Fk时，对前面k-1级及第k级强度下的坡体最大水平位移S与Fk的演化规律进行泰勒级数拟合，并将拟合曲线的各参数代入尖点突变模型，根据式(7)至式(12)求出各级强度下的相应的控制变量μ，v和最大水平位移突变特征值Δ值。

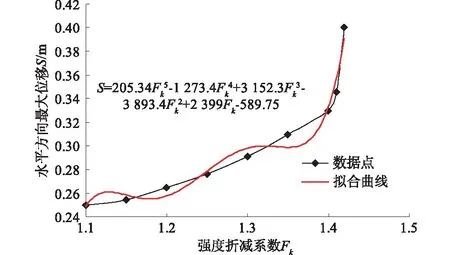
图5 最大水平位移与强度折减系数的拟合曲线

对图5中强度折减系数和最大水平位移分6～10个级数进行曲线拟合，控制变量u，v和突变特征值Δ,拟合所得结果见表3。限于篇幅，下面仅以有代表性的8，9两级拟合计算过程进行说明。

表3 不同折减系数下的控制变量和突变特征值Δ

当Fk=1.41时，对折减系数从1.1～1.41共8级强度下S与Fk进行5次多项式拟合可得：

S=45.365Fk5-276.57Fk4+672.5Fk3-

814.65Fk2+491.47Fk-117.88 。

(15)

将上述拟合曲线的各参数代入式(9)至式(12)并进行转换可得势函数的标准形式，即

(16)

从式(16)可以看出Fk取1.41时，该正则突变模型中u=-0.388 26，v=0.212 38，此时水平方向最大位移突变特征值Δ=4u3+27v2=0.983 73，土坡尚且处于稳定状态。而当Fk取为1.42时，对Fk从1.1～1.42共9级强度下S与Fk的拟合曲线(见图5)为：

S=205.34Fk5-1 273.4Fk4+3 152.3Fk3-

3 893.4 Fk2+2 399Fk-589.75 。

(17)

对式(17)求导，根据式(9)至式(12)转换成势函数的标准形式：

(18)

当Fk=1.42时，该模型中控制变量u=-0.604 48，v=0.083 26，此时Δ=4u3+27v2=-0.696 33，表明边坡发生失稳破坏，依据尖点突变模型判据可知土坡稳定安全系数为1.41。

5.2.4 各种失稳判据的比较

为了验证上述3种失稳判据判定成果可靠性，考虑到传统极限平衡法中Spencer法满足全部的力学平衡条件，理论基础较为严格，本文以Spencer法计算结果作为参考标准。采用此法计算出的土坡安全系数Fs=1.398， 3种失稳判据与其计算结果的误差分别为4.43%，1.57%，0.858%。误差分析表明数值计算不收敛判据所得结果与Spencer法偏差最大，其明显高于其他2种失稳判据求得的安全系数。进一步分析可知，数值计算收敛性受收敛限值、迭代方法、计算单元模型、边界条件及单元网格精度等多种因素综合影响，且此判据无法反映土坡变形破坏的过程，物理意义不明确，求解安全系数时带有一定的主观人为性；塑性区贯通并不意味着土坡发生失稳破坏，还要看土坡是否产生无限制的塑性变形和位移，在判定塑性区是否贯通时需要人为进行观察，其“自动化”程度不高，且要提高此判据的计算精度需要调整折减系数的增加步长值，限制了该判据的推广；而尖点突变模型判据建立了折减系数与边坡稳定状态间的定量关系，实现了失稳判据的量化，消除了人为因素的影响，其所得的安全系数与Spencer法最为接近。

6 结 语

本文通过对非线性突变理论进行系统深入地阐述，将其引入到边坡稳定性分析中，建立非均质土坡失稳破坏的数值计算模型，采用强度折减有限元法研究非均质土坡变形破坏机制。依据突变理论，建立了坡体水平方向最大位移与折减系数的尖点突变模型，以突变特征值Δ与0的关系来表征边坡所处的状态，进而对土坡安全稳定性做出评判，实现了失稳判据的量化，克服了人为因素的影响，其计算结果更加客观。结合具体的工程实例表明，采用尖点突变模型失稳判据计算出的安全系数与应用较为成熟的极限平衡Spencer法具有较好的一致性，进而验证了此判据的合理性和准确性，为非均质土坡的稳定性分析提供了一种新的定量研究途径。

[1] 赵尚毅，郑颖人，张玉芳. 有限元强度折减法中边坡失稳的判据探讨[J]. 岩土力学，2005，26(2):332-336. (ZHAO Shang-yi，ZHENG Ying-ren，ZHANG Yu-fang. Study on Slope Failure Criterion in Strength Reduction Finite Element Method[J]. Rock and Soil Mechanics，2005，26 (2): 332-336. (in Chinese))

[2] 陈力华，靳晓光. 有限元强度折减法中边坡三种失效判据的适用性研究[J]. 土木工程学报，2012，45(9): 136-146. (CHEN Li-hua，JIN Xiao-guang. Study on the Applicability of Three Criteria for Slope Instability Using Finite Element Strength Reduction Method[J]. China Civil Engineering Journal， 2012，45(9): 136-146. (in Chinese))

[3] 林 杭，曹 平，李江腾，等. 边坡临界失稳状态的判定标准[J]. 煤炭学报，2008，33(6): 643-647. (LIN Hang， CAO Ping，LI Jiang-teng，etal. The Standards for Critical Failure State of Slope[J]. Journal of China Coal Society，2008，33(6): 643-647. (in Chinese))

[4] 张培文，陈祖煜. 弹性模量和泊松比对边坡稳定安全系数的影响[J]. 岩土力学，2006，27(2): 299-303. (ZHANG Pei-wen，CHEN Zu-yu. Influences of Soil Elastic Modulus and Poisson’s Ratio on Slope Stability[J]. Rock and Soil Mechanics，2006，27(2): 299-303. (in Chinese))

[5] 赵延林，吴启红，王卫军，等. 基于突变理论的采空区重叠顶板稳定性强度折减法及应用[J]. 岩石力学与工程学报，2010，29(7): 1424-1434. (ZHAO Yan-lin，WU Qi-hong，WANG Wei-jun，etal. Strength Reduction Method to Study Stability of Goaf Overlapping Roof Based on Catastrophe Theory[J]. Chinese Journal of Rock Mechanics and Engineering，2010，29(7): 1424-1434. (in Chinese))

[6] 付成华，陈胜宏. 基于突变理论的地下工程洞室围岩失稳判据研究[J]. 岩土力学，2008，29(1): 167-172. (FU Cheng-hua，CHEN Sheng-hong. Study on Instability Criteria of Surrounding Rock of Underground Engineering Cavern Based on Catastrophe Theory[J]. Rock and Soil Mechanics，2008，29(1): 167-172. (in Chinese))

[7] 郑东健，雷 霆. 基于突变理论的高拱坝失稳判据研究[J]. 岩土工程学报，2011，33(1):23-27. (ZHENG Dong-jian，LEI Ting. Instability Criteria for High Arch Dams Using Catastrophe Theory[J]. Chinese Journal of Geotechnical Engineering，2011，33(1): 23-27. (in Chinese))

[8] 李 凯，陈国荣. 以尖点突变模型为边坡临界失稳的判据研究[J]. 桂林工学院学报，2009， 29(1): 102-105. (LI Kai，CHEN Guo-rong. Cusp Catastrophe Model for Slope Critical Failure[J]. Journal of Guilin University of Technology，2009，29(1): 102-105. (in Chinese))

[9] 张艳山，潘玉珍. 基于ABAQUS对Drucker-Prager系列准则的讨论[J]. 水电能源科学，2010，28(11): 70-71. (ZHANG Yan-shan，PAN Yu-zhen. Study on Drucker-Prager Yield Criterions Based on ABAQUS[J]. Water Resources and Power，2010，28(11):70-71.(in Chinese))

[10]郑颖人，赵尚毅，邓楚键，等. 有限元极限分析法发展及其在岩土土程中的应用[J]. 中国工程科学，2006，8(12):39-61. (ZHENG Ying-ren，ZHAO Shang-yi，DENG Chu-jian，etal. Development of Finite Element Limit Analysis Method and Its Applications in Geotechnical Engineering[J]. Engineering Science，2006，8(12): 39-61. (in Chinese))[11]史俊涛，孔思丽，任 琪. 基于强度折减有限元法的边坡稳定性影响因素敏感性研究[J]. 武汉科技大学学报，2013，36(4): 316- 320. (SHI Jun-tao， KONG Si-li， REN Qi. Studies of Sensitivities of Influence Factors on Slope Stability Based on the Shear Strength Reduction FEM[J]. Journal of Wuhan University of Science and Technology，2013，36(4): 316- 320. (in Chinese))

(编辑：黄 玲)

An Instability Criterion for Inhomogeneous Slope Based onCusp Catastrophe Theory

SHI Jun-tao1,2，KONG Si-li2，HE Jun3，HUANG Chun-hui2

(1.Department of Architecture Administration of Tianmen City, Tianmen 431700, China； 2.School of Civil Engineering, Guizhou University, Guiyang 550025, China； 3.School of Civil Engineering and Architecture, Southwest Petroleum University, Chengdu 610500, China)

In order to avoid the subjective factitiousness of instability criterions, the nonlinear catastrophe theory is applied to evaluate the stability of inhomogeneous slope. A numerical mechanical model in association with strength reduction FEM was adopted to analyze soil slope stability. Through establishing the cusp catastrophic model of the maximum horizontal displacement and strength reduction coefficient, the instability criterion was quantified as a determined catastrophe eigenvalue. Furthermore, safety factor was obtained according to the relationship between catastrophe eigenvalue of maximum horizontal displacement and zero in the presence of different strength reduction coefficients. The obtained safety factor was compared with that from other two criteria (plastic zone penetration and misconvergence) and Spencer’s procedure of limit equilibrium. Results indicate that the relation between slope stability and strength reduction coefficient can be quantified by this cusp catastrophic model and the catastrophe of slope instability process can be reflected. This instability criterion has high calculation precision and definite physical meaning.

inhomogeneous soil slope; cusp catastrophe theory; stability analysis; instability criterion; Drucker-Prager yield criteria; strength reduction method

2014-01-16；

2014-02-24

史俊涛(1987-)，男，湖北天门人，工程师，硕士，主要从事边坡稳定性、地基基础的研究，(电话)18286034129(电子信箱) ssjjtt123@sina.com。

孔思丽(1961-)，女，贵州贵阳人，副教授，主要从事岩土工程、地基基础方面的研究，(电话)18085079611(电子信箱)228812767@qq.com。

10.3969/j.issn.1001-5485.2015.05.022

2015,32(05):115-120

U416.14

A

1001-5485(2015)05-0115-06