基于上限有限元原理的双曲线强度折减法

牛 岩,谢良甫，周治宇,王永卫

(1.湖北省鄂西地质工程勘察院，湖北 宜昌 443100；2.中国地质大学(武汉)工程学院，武汉 430074；3.四川省蜀通勘察基础工程有限责任公司，成都 610000；4.中国地质大学(武汉)江城学院，武汉 430200)

基于上限有限元原理的双曲线强度折减法

牛 岩1，2,谢良甫2，周治宇3,王永卫4

(1.湖北省鄂西地质工程勘察院，湖北 宜昌 443100；2.中国地质大学(武汉)工程学院，武汉 430074；3.四川省蜀通勘察基础工程有限责任公司，成都 610000；4.中国地质大学(武汉)江城学院，武汉 430200)

相对于极限平衡法和有限元法来说，极限分析在边坡的稳定性分析中有着更严谨的理论基础和更明确的物理意义，但传统的极限分析上限法为了避免问题成为非线性规划，均是借助于超载系数来进行分析，而工程边坡用得最多的还是强度储备安全系数。针对这一问题，系统地介绍了极限分析上限有限元原理，并将强度折减技术引入到上限法，针对强度折减系数和超载系数满足双曲线的性质，用一种收敛速度更快的双曲线迭代法进行计算，克服了传统强度折减进行人工试算的不足，具有较高的收敛性。通过算例将所提方法与传统极限平衡法和有限元法进行对比，计算结果吻合度较高，说明了本方法的有效性。

极限分析；上限有限元；稳定性分析；强度折减；双曲线迭代

1 研究背景

边坡的稳定性分析一直是岩土工程领域的重要研究课题，目前比较常用的边坡稳定性分析方法主要有极限平衡法、有限元强度折减法和极限分析法。传统的极限平衡法，如Janbu法、Spencer法和Sarma法等，虽说抓住了边坡稳定破坏的主要矛盾，但其为了使不静定问题转化成静定问题，引入了大量的假设，力学上不够严密。

有限元法虽能弥补前者的不足，但在极限状态的标准方面尚存争议，是以塑性区贯通还是力不收敛作为边坡失稳破坏的判据尚未达成统一[1-2]。其实，人们最关心的并不是岩土体内部的应力场、位移场等量值的具体大小和分布情况，而是边坡是否稳定以及它的安全程度如何，破坏模式和破坏范围也是特别关心的问题。对于此类问题，极限分析则抓住了问题的关键，从极大极小原理出发，运用上限法和下限法，分别放松极限荷载的力的约束和位移的约束，寻求问题的上限解和下限解，从不同角度逼近真实解。

极限分析上限法目前已有较多学者进行了研究，陈祖煜[3]以极限分析上限理论体系为基础，推出了基于斜条分思想的斜条分上限解法，并在2000年，将塑性极限的求解范围从二维扩大到三维，对小湾高拱坝的稳定性进行了三维极限分析[4-5]；S.W. Sloan[6-7]将极限分析上限法与有限元相结合，考虑单元之间相邻边上的速度间断条件，将理想塑性材料的上限分析归结为求解一个大规模线性规划问题。H.S.Yu等[8]对上述问题进行了改进，引入了6节点三角形单元进行上限有限元计算。王均星等[9-11]从不同角度对上限有限元法进行了研究。

本文基于S.W. Sloan[6-7]的研究成果，将强度折减技术引入上限有限元法，通过调整强度参数使超载系数逼近于1[12]，从而得到强度折减系数；并且根据强度折减系数与超载系数关系近似符合双曲线函数这一特性，采用拟合双曲线插值的方法对强度折减进行求解，利用线性规划可以很快地得到边坡的强度折减系数。

2 极限分析上限法原理

2.1 概 念

上限定理可以表述为：一个受力物体，在满足速度边界条件、应变与速度相容条件的变形模式下，由外功率等于所消耗的内功率而得到的荷载，不会小于实际破坏荷载，相应的速度场称为运动许可速度场。

上限定理就是寻找满足速度相容条件下的外荷载T的极限。

(1)

2.2 上限有限元法基本公式

2.2.1 单元离散

本文用三角形单元对边坡进行离散，则单元内任一点的速度分量可表示为节点速度分量的线性函数，如式(2)：

(2)

式中：Ni为三角形单元的形函数[13]；vi是关于节点坐标的线性函数。

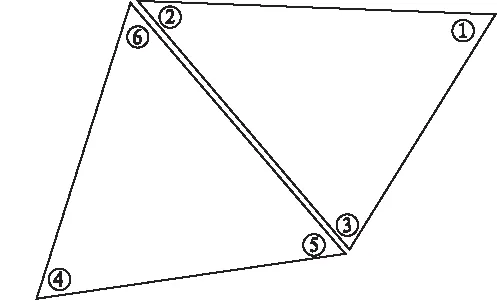
图1 上限有限元 三角形单元离散

需要指出的是，上限有限元单元离散与有限元网格稍有不同，上限元每个三角形内部节点均是独立的节点，即拥有相同坐标但属于不同单元的节点仍看作是不同的节点，如图1所示，节点3和节点5属于不同节点，同理类推到节点2和6及其他。

2.2.2 塑性流动约束条件

对平面应变问题，假设拉正压负，摩尔-库伦屈服准则可表示为

(3)

式中：c和φ分别为土体黏聚力和内摩擦角。

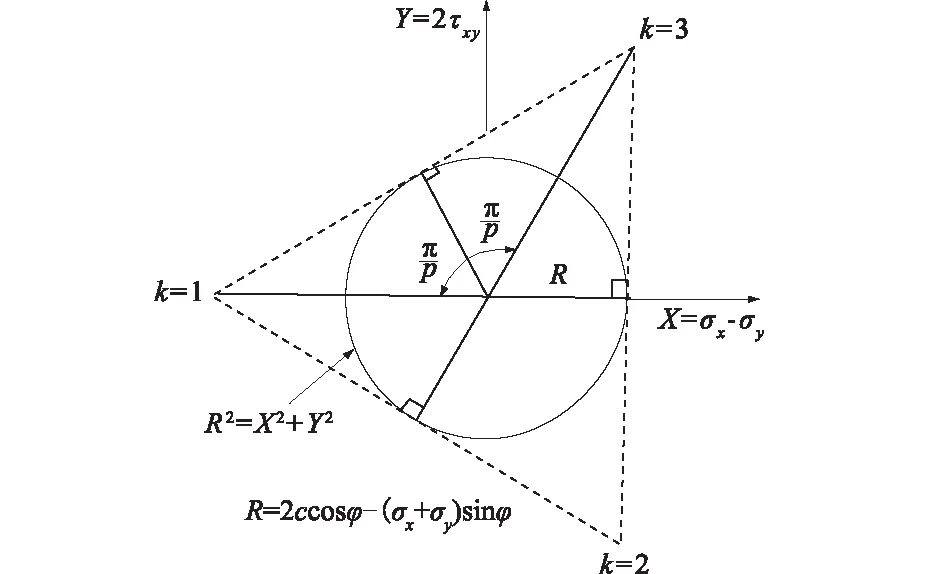
图2 线性摩尔-库伦屈服函数(p=3)

用外切正p边形去拟合屈服面，如图2所示，那么每个节点的屈服条件均可用p个线性方程代替，则F可写为

(4)

(5)

对于理想刚塑性体，相关流动法则结合线性化的摩尔-库伦屈服准则可表示为：

(6)

(7)

(8)

(9)

(10)

(11)

式中a11，a12分别为应变矩阵和屈服函数系数矩阵，具体值参见文献[6]。

2.2.3 速度间断线上塑性流动约束条件

如图3，节点1，2和节点3，4所在的速度间断线与x轴夹角为θ,则对于摩尔-库伦屈服准则，速度间断线上的法向Δv与切向Δu相对速度需满足

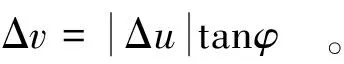
(12)

图3 三角形单元速度间断线

按照文献[7]中的方法，对每对速度间断点引入非负变量u+和u-，且满足：

(13)

(14)

于是，对于每条速度间断线，需要施加的塑性流动约束条件为：

(15)

(16)

(17)

式中a21，a23分别为坐标转换矩阵和参数矩阵，具体值参见文献[7]。

2.2.4 速度边界条件

(18)

(19)

式中a31为坐标转换矩阵，参见文献[6]。

2.2.5 外力功率与内部耗散功率

2.2.5.1 单元内部耗散功率

每个单元内部耗散功率P为

(20)

式中A为三角形单元面积，将式(6)至式(8)代入上式，可得

(21)

将上式写成矩阵的形式即为

(22)

c2的表达式见文献[7]。

2.2.5.2 速度间断线上的耗散功率

每条速度间断线上的耗散功率Pd为

(23)

式中l为间断线长度。令Δu=u++u-,则上式写成矩阵形式即

(24)

c3的表达式见文献[7]。

2.2.5.3 外力功率

外力功率是塑性流动刚发生时，所有外部荷载对破坏区域的速度场所做的功率。现仅以体力为例进行说明，如式(25)：

(25)

对于三角形单元，由于体力在单元内部为线性分布，于是上式可写成如下形式：

(26)

其中，c1=-γ/3[0A0A0A]，A为三角形单元的面积。

3 上限有限元法线性规划模型

在岩土工程领域，一般采用安全系数来评价边坡的稳定性等级，常用的安全系数有超载系数和强度折减系数。虽然对于工程边坡来说，最常用的还是强度折减系数，但如果直接采用强度折减系数，那么整个模型将转化成为一非线性规划问题，这就给计算效率造成了影响。为了避免此问题发生，目前上限有限元计算采用较多的仍是超载系数。

当只考虑体力时，设超载系数为λ，则上限有限元法的目标函数可以写成

(27)

由于我们求解的是破坏时结构的破坏形式，它仅与x1的相对大小有关，因此令：

(28)

此时，整个上限有限元形成的线性规划模型为：

Min:λ=c2x2+c3x3。

(29)

(30)

4 强度折减系数及双曲线迭代

强度折减的概念是O.C.Zienkiewicz等[14]在20世纪70年代首次提出，基本思想就是不断按照式(24)对强度参数c和φ进行折减直到达到边坡的极限状态为止，折减系数K即是安全系数。

(31)

对上限有限元法，为了既能求出强度折减系数又避免问题转化为非线性规划，本文引入文献[12]中对下限有限元所采用的方法，通过调整强度参数使得超载系数逼近于1，此时的折减系数即为最终强度折减系数。

图4 强度折减双曲线法 迭代过程

李春光等[15]对强度折减法结合极限分析下限法提出了双曲线迭代形式，并与二分法和割线法做了对比等，证明了收敛阶为二次收敛的双曲线迭代有着更高的收敛速度。本文将此方法引入极限分析上限法，对比了不同网格背景、不同外接屈服多边形边数下边坡的强度折减系数，较快地求得了边坡的安全系数和极限状态失稳速度场。

据文献[15]，强度折减系数K与超载系数λ满足这样的关系，如图4所示：

(1) 当K趋向于无穷大时，λ趋向于0；

(2) 当K趋向于0时，λ趋向于无穷大。

而双曲线函数恰恰满足这2个特点，因此，可以构造如下函数，来对强度折减系数进行迭代求解：

(32)

式中a和b为双曲线系数。

本文采用如下建议迭代过程：

(1) 给定初始的强度折减系数K1和K2，代入上限有限元法求出λ1和λ2；

(2) 将(K1,λ1)和(K2,λ2)代入双曲线函数，可得

(33)

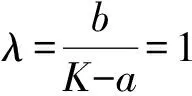
(34)

5 算 例

本文算例是由ABAQUS软件进行三角形单元离散剖分，再将节点信息导入Matlab软件进行计算。

一均质边坡，引自文献[2]，坡比为1∶2，材料参数见表1。为了比较不同网格背景下上线有限元法的计算结果，本文采用2套网格进行分析，如图5，网格由疏到密。

图5 边坡网格划分

重度γ/(kN·m-3)黏聚力c/kPa内摩擦角φ/(°)坡高H/mcγH201020100．05

分别采用正3边形、5边形、10边形、15边形和20边形来进行屈服面逼近。得到的安全系数如表2。

表2 不同边数正多边形逼近时的安全系数

图6 安全系数F与 多边形边数p的关系图

从表2可以看出，随着外接正多边形边数的增多，安全系数逐渐收敛到真实值，文献[2]对本算例基于强度折减有限元给出的建议解为1.40，用极限平衡法Bishop和Morgenstern算出的安全系数为1.380，这均与本文用上限法采用较密网格算出的结果1.41比较接近，当采用较疏网格时，得到的安全系数偏大，这与上限有限元法的性质是相吻合的，证明了本文方法的正确性。

本算例采用双曲线强度折减关系，当p=20时，较疏和较密网格模型均是迭代5次，即可达到收敛；图7为2种网格极限状态边坡失稳速度场。从图7中可以清晰看出边坡的滑动模式和滑动面，这可为后续的边坡支护提供帮助。

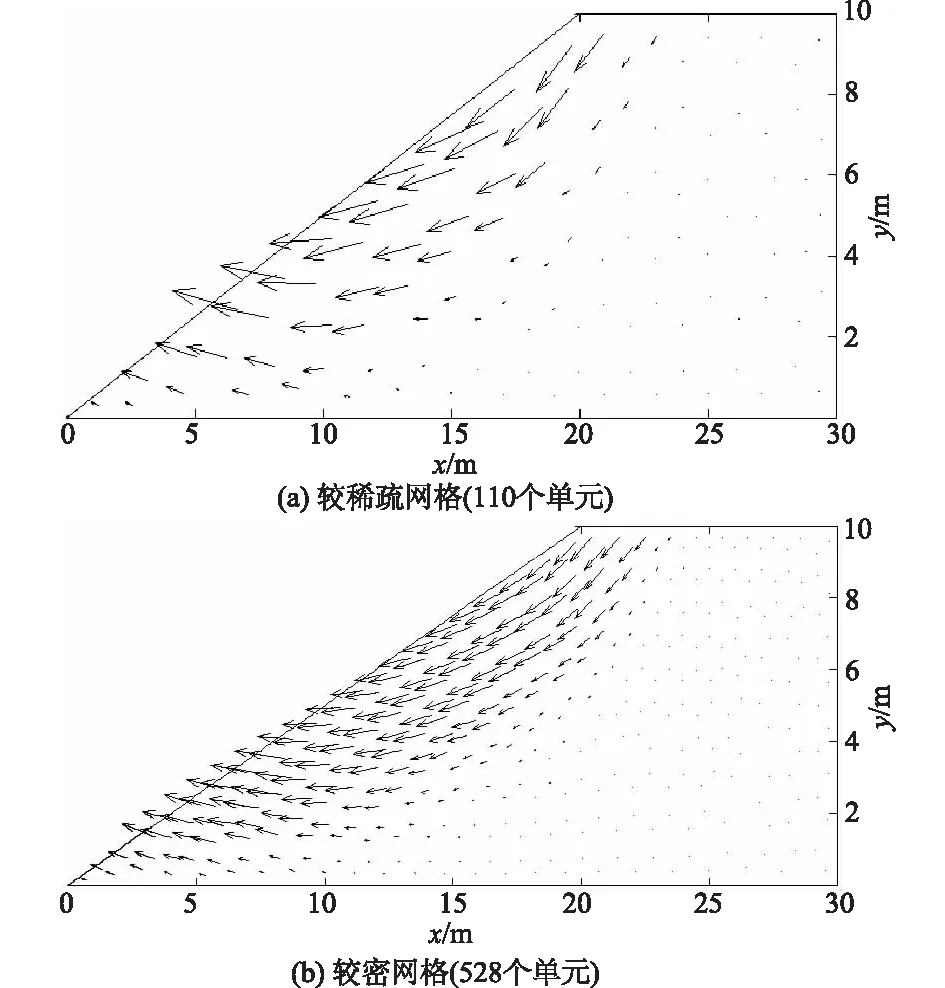
图7 边坡极限状态失稳速度场

6 结 论

(1) 边坡稳定的极限分析法有严谨的理论基础和明确的物理意义，本文在Sloan等人的工作基础上，基于线性规划模型，采用Matlab编制上限有限元程序，针对强度折减系数和超载系数的关系近似为双曲线这一性质，用双曲线迭代法进行计算，该算法收敛速度快，且精度较高。

(2) 通过经典算例对本文提出的方法进行了验证，随着外切屈服圆多边形边数的增多，得到的解逐渐收敛于真实解，且当多边形边数p达到一定值后，再增加p的值，计算结果变化不大，从本文算例可以看出p=15时已经达到了较高的收敛效果。将得到的数值解与其他方法得到的解进行了比较，吻合度较高，说明了本文方法的正确性和可靠性。

[1] 宋二祥. 土工结构安全系数的有限元计算[J]. 岩土工程学报, 1997, 19(2):1-7. (SONG Er-xiang. Finite Element Analysis of Safety Factor for Soil Structures[J]. Chinese Journal of Geotechnical Engineering,1997,19(2): 1-7.(in Chinese))[2] GRIFFITHS D V, LANE P A. Slope Stability Analysis by Finite Elements[J]. Geotechnique, 1999, 49(3):387-403.

[3] 陈祖煜.土力学经典问题的极限分析上、下限解[J].岩土工程学报，2002，24(1)：1-11.(CHEN Zu-yu.Limit Analysis for the Classic Problems of Soil Mechanics[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(1): 1-11.(in Chinese))[4] 陈祖煜，汪小刚，杨 健,等.岩质边坡稳定分析[M」.北京:中国水利水电出版社，2005. (CHEN Zu-yu, WANG Xiao-gang, YANG Jian,etal. Stability Analysis of Rock Slope[M]. Beijing: China Water Power Press, 2005.(in Chinese ))

[5] 陈祖煜.土质边坡稳定分析[M].北京:中国水利水电出版社，2003. (CHEN Zu-yu. Stability Analysis of Soil Slope[M]. Beijing: China Water Power Press, 2003. (in Chinese ))

[6] SLOAN S W. Upper Bound Limit Analysis Using Finite Element and Linear Programming[J]. International Journal of Analytical Methods in Geomechanics, 1989, 13(3)：263-282.

[7] SLOAN S W. Upper Bound Limit Analysis Using Discontinuous Velocity Fields [J]. Journal of Computer Methods in Applied Mechanics and Engineering，1995，127(4)：293-314.

[8] YU H S，SLOAN S W，KLEEMAN P W. A Quadratic Element for Upper Bound Limit Analysis[J]. Engineering Computations，1994，11(3)：195-212.

[9] 王均星，王汉辉，张优秀, 等.非均质土坡的有限元塑性极限分析[J].岩土力学，2004，25(3):415-421.(WANG Jun-xing, WANG Han-hui, ZHANG You-xiu,etal. Plastic Limit Analysis of Heterogeneous Soil Slope Using Finite Elements[J]. Rock and Soil Mechanics, 2004, 25(3):415-421.(in Chinese))

[10]王汉辉，王均星，王开治.边坡稳定的有限元塑性极限分析[J].岩土力学，2003，24(5):733-738. (WANG Han-hui, WANG Jun-xing, WANG Kai-zhi. Plastic Limit Analysis of Slope Stability Using Finite Element[J]. Rock and Soil Mechanics, 2003，24(5): 733-738. (in Chinese))

[11]杨 峰,阳军生,张学民. 基于线性规划模型的极限分析上限有限元的实现[J]. 岩土力学, 2011, 32(3): 914- 921. (YANG Feng, YANG Jun-sheng, ZHANG Xue-min. Implementation of Finite Element Upper Bound Solution of Limit Analysis Based on Linear Programming Model[J]. Rock and Soil Mechanics, 2011, 32(3): 914-921. (in Chinese))[12]李国英, 沈珠江.下限原理有限单元法及其在土工问题中的应用[J]. 岩土工程学报, 1997, 19(5): 84-89. (LI Guo-ying, SHEN Zhu-jiang. Application of Lower Bound Limit Finite Element to Geotechnical Problems[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(5): 84-89. (in Chinese))[13]朱伯芳. 有限单元法原理与应用[M].北京：中国水利水电出版社，2009. (ZHU Bo-fang. Principle and Application of Finite Element[M]. Beijing: China Water Power Press, 2009.(in Chinese))

[14]ZIENKIEWICZ O C，HUMPHESON C，LEWIS R.W. Associated and Non-associated Visco-plasticity and Plasticity in Soil Mechanics[J]. Geotechnique，1975，25(4)：671-689.

[15]李春光，朱宇飞，刘 丰,等. 基于下限原理有限元的强度折减法[J]. 岩土力学，2012,33(6):1816-1821. (LI Chun-guang, ZHU Yu-fei, LIU Feng,etal. Evaluation of Strength Reduction Factor by Lower Bound Limit Analysis Using Finite Element Method[J]. Rock and Soil Mechanics, 2012,33(6):1816-1821.(in Chinese))

(编辑：王 慰)

A Strength Reduction Method of Hyperbolic IterationBased on Upper Bound Finite Element

NIU Yan1,2, XIE Liang-fu2, ZHOU Zhi-yu3,WANG Yong-wei4

(1.West Hubei Geological Engineering Investigation Institute, Yichang 443100, China; 2.Faculty of Engineering, China University of Geosciences, Wuhan 430074, China; 3.Sichuan Shutong Geotechnical Investigation and Foundation Engineering Company, Chengdu 610000, China; 4.Jiangcheng College, China University of Geosciences, Wuhan 430200, China)

Compared with limit equilibrium method and finite element method, limit analysis has a more rigorous and precise theoretical basis and clearer physical meaning in slope stability analysis. But traditional limit upper bound relies on the overload factor to avoid nonlinear programming whereas most engineering slopes are analyzed by using the factor of strength reduction. In view of this, we introduce the principle of limit upper bound of finite element analysis and introduce the strength reduction factor into the limit upper bound method. Since the relationship between strength reduction coefficient and overload coefficient is approximately hyperbolic, we present a hyperbolic iteration method to solve the strength reduction factor. This method has a faster convergence speed, and overcomes the shortage of traditional strength reduction method which needs artificial trials. The effectiveness of this method is proved by a numerical example compared with the limit equilibrium method and finite element method.

limit analysis; upper bound finite element; stability analysis; strength reduction; hyperbolic iteration

2013-10-28；

2013-11-18

牛 岩(1984-)，男，湖北宜昌人，助理工程师，硕士，主要从事工程地质方面的研究，(电话)13886691536(电子信箱)2842877132@qq.com。

10.3969/j.issn.1001-5485.2015.05.024

2015,32(05):127-131,136

TU42

A

1001-5485(2015)05-0127-05