基于激光跟踪仪的六自由度模块化机器人运动学标定*

王艳孟，石成江，王殿君，刘淑晶，李 强，张义万

(1.辽宁石油化工大学 机械工程学院，辽宁 抚顺 113001；2.北京石油化工学院 机械工程学院，北京 102617)

基于激光跟踪仪的六自由度模块化机器人运动学标定*

王艳孟1，石成江1，王殿君2，刘淑晶2，李 强2，张义万1

(1.辽宁石油化工大学 机械工程学院，辽宁 抚顺 113001；2.北京石油化工学院 机械工程学院，北京 102617)

在充分调研国内外机器人标定方法的基础上，提出了一种基于激光跟踪仪的机器人标定的方法，即直接标定法。运用微分变换方法建立了六自由度模块化机器人误差模型，并对建立的误差模型进行验证。利用激光跟踪仪直接测量机器人位姿进行标定试验，确定机器人末端位姿与运动学参数误差的关系，把得到的机器人运动学几何参数偏差补偿到控制系统软件中，对其中的运动学方程加以修正，然后对机器人进行二次标定。标定前后数据对比证明，机器人运动精度提升了50%。

激光跟踪仪；直接标定法；误差模型；运动学方程

机器人在制造装配过程中容易产生一些误差，这些误差对机器人的运动精度会有较大的影响，所以减小误差对提高机器人运动精度至关重要。对机器人进行标定的目的是了解末端位姿与运动学几何参数误差之间的准确关系。在机器人加工制造和装配过程中会使连杆长度参数和连杆偏置参数产生误差。相邻直线之间的平行度和垂直度会产生连杆扭角误差。在机器人装配过程中，由于电动机编码器的零点与机器人三维模型中关节的旋转零位不在同一轴线上，会产生关节角误差。为了提高机器人运动精度，需要通过机器人标定对这些参数进行补偿[1-2]。

1 六自由度模块化机器人运动学模型

1.1 机器人关节结构

六自由度模块化机器人在机械系统设计过程中运用了模块化的设计思想[3-4]。机器人由6个不同尺寸和构型的关节模块组成，各模块之间采用统一的接口连接， 通过增减模块数量和更换不同功能的模块，可快速装配出符合工作要求的机器人。每一个模块都可以单独控制运动，模块中包含旋转运动和回转运动2种形式，将6个模块组合起来构成六自由度模块化机器人，其构型与六自由度工业串联型关节机器人类似。六自由度模块化机器人的UG三维图和实物图如图1所示。

图1 六自由度焊接机器人外形图

1.2 机器人运动学模型

采用D-H法构建机器人连杆坐标系，可得到4个连杆参数：连杆长度ai-1、连杆扭角αi-1、连杆距离di和关节转角θi。机器人连杆参数见表1，机器人连杆的D-H坐标系如图2所示。

表1 机器人连杆参数表

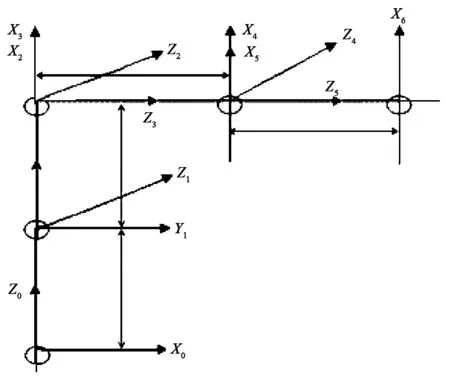
图2 机器人连杆D-H坐标系

1.3 机器人运动学分析

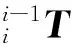
(1)

式中，cθi为cosθi；sθi为sinθi;cαi为cosαi;sαi为sinαi。

同理可知，第i个坐标系的表达式为：

(2)

由表1和式2可得：

(3)

(4)

(5)

(6)

(7)

(8)

式中，Ci为cosθi；Si为sinθi。

将6个连杆矩阵连乘，可得：

(9)

方程中的px、py、pz分别代表机器人的末端位置坐标，由于方程计算量较大，所以借助MATLAB软件对机器人运动学方程进行求解。

2 六自由度模块化机器人运动学标定

建立机器人运动学模型的目的是找出机器人各几何参数与机器人末端执行器位置和姿态之间的函数关系式，其中必然包含机器人的几何结构参数。在运动学模型的求解中，因为是理论研究，所以没有考虑误差；但是，在实际操作和加工过程中是存在误差的，机器人运动学标定就是利用某种算法标识出机器人运动学参数误差，并对其进行修正[5]。

2.1 建立误差模型

本文采用微分变换思想对机器人误差进行建模。

由上述机器人各关节变换矩阵连乘可得出其末端位姿。设：

P=F(a,d,α,θ)

(10)

则实际制造装配完成的机器人末端位姿为：

P′=F(a+Δa,d+Δd,α+Δα,θ+Δθ)

(11)

进而得到机器人实际与理论位姿的误差为：

ΔP=P-P′

(12)

因为得到的误差数值较小，所以可以将得到的误差进行简化，从而得到相应的线性方程。简化后得到的结果为：

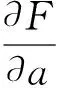
(13)

对于六自由度模块化机器人，式13中∂a表示∂a0、∂a1、∂a2、∂a3、∂a4、∂a5；∂α表示∂α0、∂α1、∂α2、∂α3、∂α4、∂α5；∂d表示∂d1、∂d2、∂d3、∂d4、∂d5、∂d6；∂θ表示∂θ1、∂θ2、∂θ3、∂θ4、∂θ5、∂θ6。

将式13用矩阵表达为：

ΔP=JδΔδ=P-P′

(14)

(15)

则误差系数矩阵可表达为：

(16)

2.2 标定试验

本文的标定试验采用直接标定法对六自由度模块化机器人进行标定。直接标定法就是应用高精度测量仪器测得机器人末端坐标，将坐标代入到误差模型中求得机器人几何参数误差，从而建立起机器人末端坐标与运动学参数误差的函数关系，把得到的Jδ几何参数误差补偿到控制系统软件中[6]。

试验中应用的是美国FARO公司制造的Xi型激光跟踪仪(见图3)，这种激光跟踪仪的测量精度比六自由度模块化机器人精度高很多，可以保证标定试验的准确性[7-8]。

调制比m=1时,从直流电压利用率方面分析,采用SVPWM调制方式比SPWM调制模式提高15%以上[13]。

图3 美国FARO激光跟踪仪

利用激光跟踪仪测量的数据包括三部分：机器人基坐标系的测量、机器人基本参数的测量和机器人实际位置的测量。机器人基坐标系测量是为了在激光跟踪仪内建立机器人的坐标系；机器人基本参数测量主要是为了得到机器人的运动学几何参数误差；通过机器人实际位置的测量可确定机器人实际位置与理论位置的偏差。

通过上述测量的数据可以验证误差模型的正确性。将测量得到的运动学几何参数误差代入到误差模型中，可得到机器人理论的位置误差，将理论位置误差与测量得到的位置误差进行对比(见表2)，可以看出，偏差在合理范围之内，证明了误差模型的正确性。将测量得到的位置误差代入到误差模型，可得到理论的运动学几何参数误差，将其与测量得到的实际运动学几何参数误差对比(见表3)，可进一步证明误差模型的正确性。

表2 实际误差与理论误差数据对比

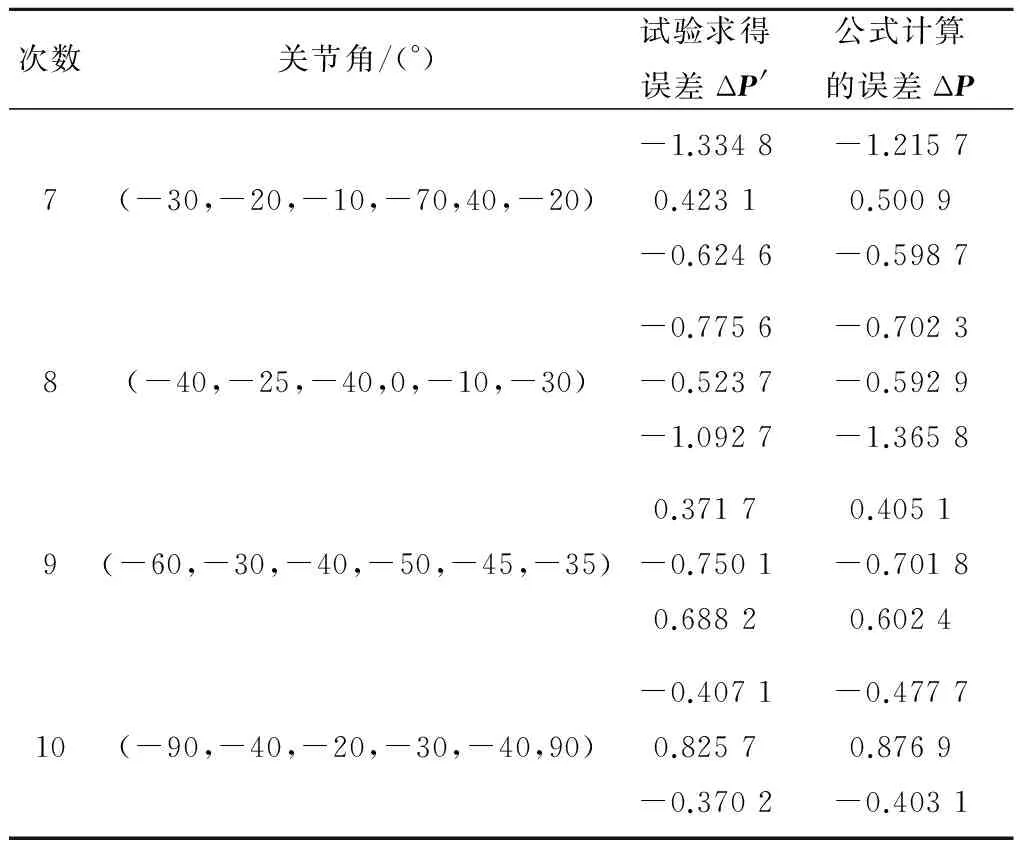
续表

2.3 误差补偿

将得到的机器人运动学几何参数偏差补偿到控制系统软件中的运动学方程，然后运用同样的方法测量机器人末端位置的基坐标，得到补偿后的机器人误差(见表4)，将其与补偿前的数据(见表5)进行对比。

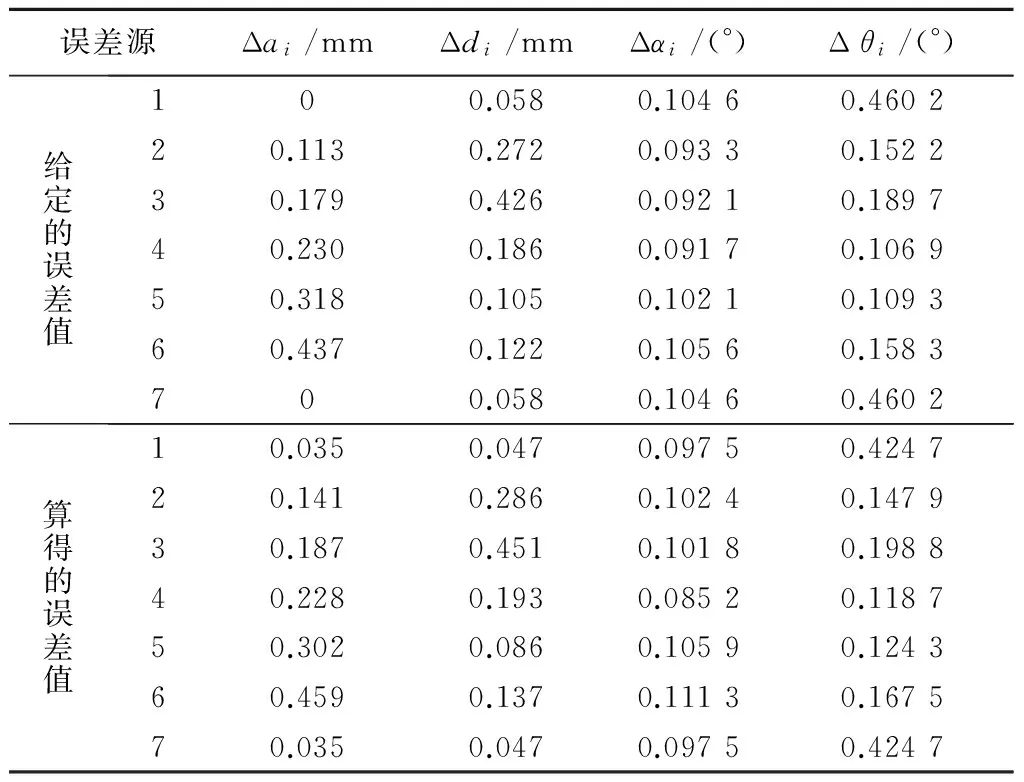
表3 测量几何参数与理论几何参数数据对比

表4 补偿后机器人误差

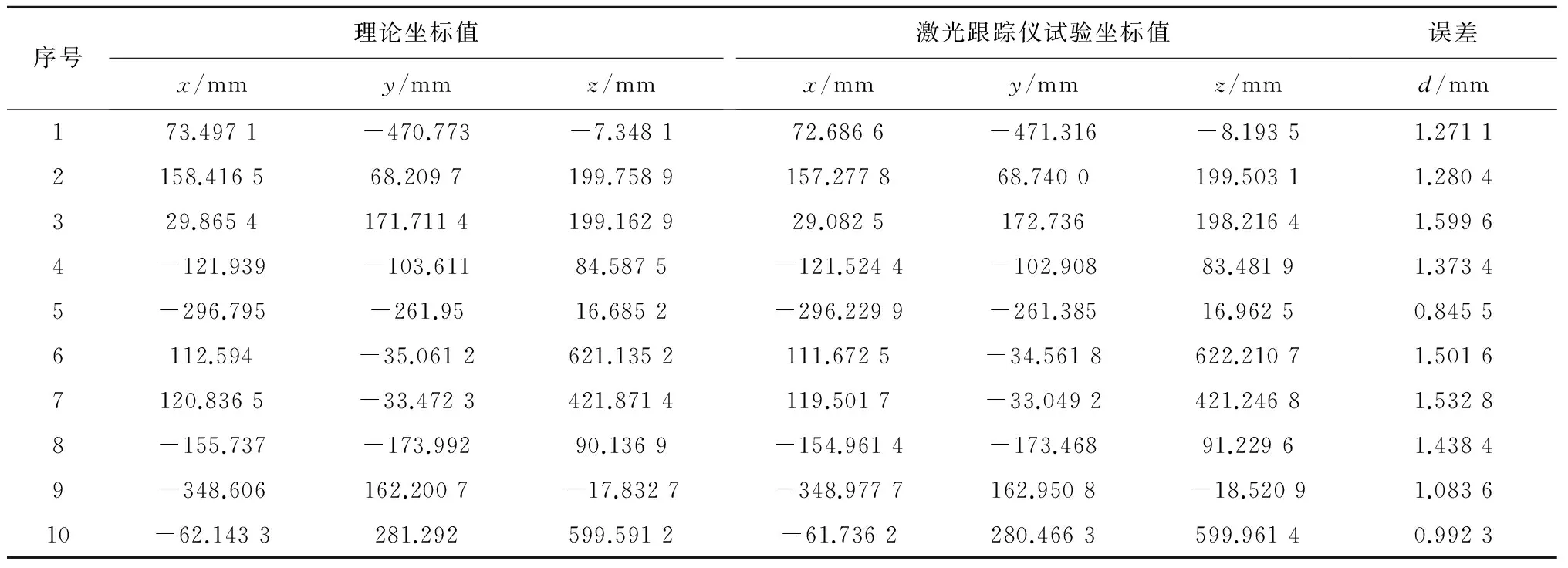
表5 补偿前机器人误差

观察表4可知，经过补偿后的机器人的末端位置坐标值与理论坐标值的偏差减小，说明机器人的运动精度有所提高，证明误差补偿具有意义；对比表4和表5的误差数据可知，将补偿后标定试验得到的误差数值与标定前的误差值相比，机器人末端位置误差值减小了50%，达到了标定试验的预期目标。

3 结语

1)运用激光跟踪仪对机器人进行运动学标定试验，通过试验测得的数据对已建立的误差模型和试验方案的可行性、合理性进行了验证，证明了用微分变换的方法推导出机器人误差模型是正确的。

2)通过对机器人控制系统中的运动学参数进行补偿，机器人的运动精度提高了50%。

[1] 叶声华，王一，任永杰，等. 基于激光跟踪仪的机器人运动学参数标定方法[J]. 天津大学学报，2007(2)：202-205.

[2] 赵伟.基于激光跟踪仪测量的机器人定位精度提高技术研究[D].浙江：浙江大学，2013.

[3] 王永甲.可重构模块化机器人构型设计理论与运动学研究[D].南京：南京理工大学，2008.

[4] 王卫忠.可重构模块化机器人系统关键技术研究[D].哈尔滨：哈尔滨工业大学，2007.

[5] 王品, 廖启征, 庄育锋, 等．一般7R串联机器人标定的仿真与实验[J].机器人,2006, 28(5):483-487.

[6] 龚星如，沈建新，田威，等.工业机器人定位误差补偿方法与实验研究[J].机械与电子，2011，19(7)：64-67.

[7] 张振久，胡泓，刘欣.基于激光跟踪仪的机床导轨系统误差检测[J].中国激光，2012，38(9)：159-164.

[8] 齐立哲，陈磊，王伟余，等.基于激光跟踪仪的机器人误差测量系统标定[J].制造技术与机床，2012(10)：90-94.

*国家“八六三”高技术项目(2012AA041402)北京石油化工学院大学生研究训练(URT)计划项目(2014J00118)

责任编辑郑练

KinematicsCalibrationSixDegreesofFreedomModularRobotbasedonLaserTracker

WANG Yanmeng1, SHI Chengjiang1, WANG Dianjun2, LIU Shujing2, LI Qiang2, ZHANG Yiwan1

(1.Mechanical Engineering Academy, Liaoning Shihua University, Fushun 113001, China;2.Mechanical Engineering Academy, Beijng Institute of Petro-chemical Technology, Beijing 102617, China)

On the basis of the full research on domestic and overseas calibration methods of robots, a robot calibration method based on laser tracker is proposed, and it is named the direct calibration method. Use differential transform method to establish six degrees of freedom of the modular robot error model, and verify the error model. Use laser tracker directly measure the position and posture to do robot calibration experiment, determine the relationship of the position and posture of the end of the robot and the error of kinematics parameter. Put the error of robot kinematics geometry parameters into the control system software to compensate the original values, on which the kinematics equation is modified. Then we calibrate the robot in the second time. The contrast of data before and after calibrating proves that the robot motion accuracy has increased by 50%.

laser tracker, direct calibration method, error model, kinematics equation

TP 242.6

:A

王艳孟(1987-)，男，硕士研究生，主要从事机电一体化和机器人技术等方面的研究。

王殿君

2014-11-27