船载雷达天线与航姿分系统安装精度研究

汪 洋，赵伊宁，杜以林

(1.中国人民解放军 92941部队，辽宁 葫芦岛 125001；2.中国人民解放军装备学院 研究生管理大队，北京 101416；3.北京机电工程研究所，北京 100074)

船载雷达天线与航姿分系统安装精度研究

汪 洋1，赵伊宁2，杜以林3

(1.中国人民解放军 92941部队，辽宁 葫芦岛 125001；2.中国人民解放军装备学院 研究生管理大队，北京 101416；3.北京机电工程研究所，北京 100074)

建立了船载雷达天线安装系统误差与目标成功捕获概率间的关系表达式，给出了雷达天线应满足的安装精度要求。利用船载地理系和甲板系间的坐标变换关系以及2种坐标系下的方位角、俯仰角计算公式，通过蒙特卡洛仿真得到了船载分系统的安装精度要求。为船载天线和航姿分系统的安装与标校提供了理论依据。

船载雷达天线；航姿分系统；安装精度；蒙特卡洛仿真

Beijing 101416,China；3.Beijing Research Institute of Mechanical and Electrical Engineering, Beijing 100074，China)

船载雷达天线作为船载雷达系统的关键部件，在探测、通信和制导等方面发挥着重要作用。实际安装过程中，船载雷达天线座往往不能保证和水平基准面完全水平，并且存在和船艏轴线不一致的现象，这将对探测目标的指向精度产生直接影响。船舶在航行时会发生横摇、纵摇及航向的改变，一般采取两轴稳定系统或者无机械稳定平台的三轴稳定系统来有效隔离船体的摇摆。稳定系统利用航姿分系统提供的纵摇角、横摇角和航向角信息，通过坐标变换技术在雷达天线方位和俯仰轴上进行实时的角度补偿，因此，航姿分系统的安装误差会对雷达波束的稳定指向造成影响。

文献[1]分析了船载雷达天线非理想安装对系统测向误差产生的影响，并且给出了一种误差补偿方法，但是缺乏对天线安装精度的定量分析。文献[2]、文献[3]介绍了船载雷达系统常用的坐标变换公式以及相应坐标系下方位角和俯仰角的计算方法，为雷达天线的指向计算奠定了理论基础，然而并没有深入分析航姿分系统的安装精度要求。本文先从系统成功捕获目标的角度出发，研究由天线非理想安装引入的系统误差对捕获成功概率的影响，进而得到天线座安装应满足的精度要求；然后运用船舶地理坐标系和甲板坐标系之间的变换公式，通过软件仿真分析航姿分系统应满足的安装精度要求。

1 船载雷达天线安装精度分析

船载雷达天线的安装精度直接影响系统的指向精度及捕获概率。假定误差是正态平稳随机过程，且连续捕获概率近似服从泊松分布，则连续捕获成功概率为：

(1)

(2)

(3)

式中，Bn是伺服带宽。

假定系统参数选取如下：σ=0.35°，Bn=2.0 Hz，R1=1.6°，T=0.6 s，由式1～式3计算得到，天线安装系统误差q1与系统捕获成功概率P关系如图1所示，可以看出当天线座方位安装精度高于0.35°时，可保证捕获成功概率>99%。

图1 天线安装系统误差对系统捕获成功概率的影响

2 船载航姿分系统安装精度分析

船载航姿分系统的主要功能是提供进行船舶地理坐标系与甲板坐标系之间转换所需要的航向、横摇和纵摇角度信息。船舶地理坐标系和甲板坐标系的示意图如图2所示，图2中船舶地理坐标系XdYdZd的原点O位于船体摇摆中心，OXd轴平行于水平面指向正东，OYd轴平行于水平面指向正北，OZd轴垂直于水平面指向天顶；船舶甲板坐标系XjYjZj是以甲板平面为基准，OYj轴平行于艏艉线指向船艏，OXj轴与OYj轴垂直指向右舷。

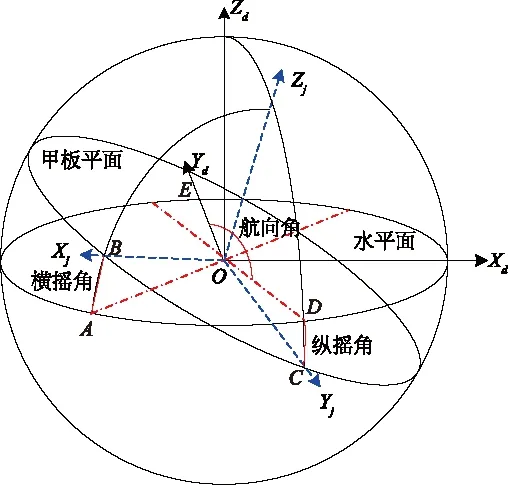
图2 船舶地理坐标系和甲板坐标系示意图

大地角转换为甲板角的公式为：

(4)

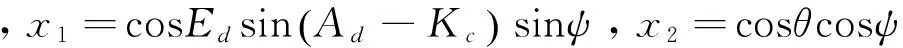
甲板角转换为大地角的公式为：

(5)

式中，y1=sinEjcosψcosθ，y2=-cosEjsinAjsinψcosθ，y3=cosEjcosAjsinθ，y4=(cosKcsinψ-sinKcsinθcosψ)sinEj，y5=sinKccosθcosEjcosAj,y6=(sinKcsinθsinψ+cosψcosKc)sinEj,y7=cosKccosθcosEjcosAj,y8=-(cosKcsinθcosψ+sinKcsinψ)sinEj,y9=(cosKcsinθsinψ+cosψcosKc) cosEjsinAj。

航姿分系统总精度应满足坐标变换后的精度高于天线波束角的1/10，这样才能保证系统的捕获要求。为了给出航姿分系统航向角、横摇角和纵摇角的具体精度要求，这里采用蒙特卡洛仿真方法[5]，将航向角、横摇角和纵摇角视作随机变量，通过统计试验和式4、式5的计算加以求解。坐标变换后的误差大小用均方根值来衡量，其计算公式为：

(6)

仿真试验中航向角、横摇角和纵摇角均设置成均值为0的正态分布，方差与精度值相等，横摇角和纵摇角精度保持一致。船舶地理坐标系到船舶甲板坐标系变换时不同横摇、纵摇和航向精度对应的方位角和俯仰角均方根误差结果如图3所示，可以看出横摇、纵摇精度对方位角均方根误差影响甚微，特别是在航向精度较高的情况下，俯仰角均方根误差随着横摇、纵摇和航向精度的降低而增加；当航向精度从0.15°变化到0.45°时，方位角均方根误差显著增加而俯仰角均方根误差逐渐增大。从船舶甲板坐标系变换到船舶地理坐标系时不同横摇、纵摇和航向精度对应的方位角和俯仰角均方根误差结果如图4所示，可以看出横摇、纵摇精度对方位角和俯仰角均方根误差影响很小，这种变化趋势与式5一致；方位角和俯仰角均方根误差随着航向精度的降低而增大。

图3 船舶地理坐标系到船舶甲板坐标系变换时不同横摇、纵摇和航向精度对应的方位角和俯仰角均方根误差

图4 船舶甲板坐标系到船舶地理坐标系变换时不同横摇、纵摇和航向精度对应的方位角和俯仰角均方根误差

综合图3和图4的仿真结果，可以得出如下结论：在航向精度≤0.30°，横摇和纵摇精度≤0.05°的条件下，由坐标变换引入的方位角和俯仰角均方根误差分别<0.29°和0.06°；因此，航姿分系统安装后的总精度>0.30°，即可保证天线波束的指向精度。

3 结语

针对船载雷达系统的天线波束稳定指向，本文提出了雷达天线和航姿分系统应满足的安装精度要求。给出了天线安装精度与目标成功捕获概率间的表达式，分析了由天线非理想安装产生的系统误差对目标成功捕获概率的影响。利用船载地理坐标系和船载甲板坐标系间的变换公式及相应坐标系下方位角和俯仰角的计算方法，通过蒙特卡洛仿真得到了横摇、纵摇和航向角精度对方位角和俯仰角均方根误差产生的影响，进一步给出了航姿分系统的安装精度要求。本文关于安装精度要求的研究，对于船载天线座和船载分系统设备的安装与标校具有重要的指导意义。

[1] 杜永强.船载雷达天线安装非理想引入的测向误差分析[J].现代雷达，2000，22(4)：61-66.

[2] 曹正才.船载雷达常用稳定方式坐标变换[J].雷达与对抗，2010，30(1):47-52.

[3] 张志远,罗国富.船舶姿态坐标变换及稳定补偿分析[J].船舶科学技术,2009,31(4):34-40.

[4] 王航宇,王士杰,李鹏.船载火控原理[M].北京:国防工业出版社,2006.

[5] 方再根.计算机模拟和蒙特卡洛方法[M].北京:北京工业学院出版社,1998.

责任编辑彭光宇

ResearchontheSettingPrecisionofShip-borneRadarAntennaandAttitudeandHeadingSubsystem

WANG Yang1,ZHAO Yining2,DU Yilin3

(1.92941 Unit of PLA, Huludao 125001,China；2.Department of Graduate Management, Academy of Equipment of PLA,

The formula describing the relation between setting system error of ship-borne radar antenna and successful acquisition probability of target is established, and the setting precision requirement of radar antenna is analyzed by the formula. Meanwhile, using the coordinate transformation between ship-borne geographic and deck coordinate systems and the calculation expressions of azimuth and elevation angle in the two coordinate systems, the setting precision requirement of ship-borne attitude and heading subsystem is obtained with the help of Monte Carlo simulation. Provide a theoretical basis for the install and calibration of ship-borne antenna and attitude and heading subsystem.

ship-borne radar antenna, attitude and heading subsystem, setting precision, Monte Carlo simulation

U 665

:A

汪洋(1969-)，男，高级工程师，硕士，主要从事测量与控制及雷达等方面的科研及管理工作。

2014-12-09