复合材料层合板渐进损伤非线性失效分析

胥玉震

(中国人民解放军91049部队，山东 青岛 266102)

复合材料层合板渐进损伤非线性失效分析

胥玉震

(中国人民解放军91049部队，山东 青岛 266102)

复合材料由于具有比强度大、比刚度高、破损安全性好和可设计性强等优点，在航空航天等工程中应用非常广泛，对其材料结构的损伤累计及失效规律等力学行为进行分析研究，具有重大的工程价值。采用有限元技术，结合渐进损伤分析(PDA)方法，以含有中心贯穿裂纹的复合材料层合板为研究对象，并通过对有限单元中材料点的刚度进行折减，模拟了复合材料损伤演化的过程。该方法能清楚地再现承载层合板内部发生损伤之后载荷的重新分布和损伤的相互作用及扩展过程，并预测出了层合板的局部和整体变形以及最终破坏载荷。试验表明，预测结果与试验结果基本吻合。

复合材料；渐进损伤；失效分析；有限元分析

复合材料由于具有比强度、比刚度高、破损安全性好和可设计性强等优点，在航空航天等工程中应用非常广泛，对其材料结构的损伤累积及失效规律等力学行为进行分析研究，具有重大的工程价值[1-3]。纤维增强复合材料层合板在静载作用下的破坏是一种不同形式损伤(基体开裂、纤维断裂、基纤剪切和分层等)不断累积，结构刚度不断退化，载荷不断重新分配以及承载能力不断降低的复杂非线性逐渐劣化失效的过程。

本文以含有中心贯穿裂纹的复合材料层合板为研究对象，进行合理的简化假设，利用有限元技术，并结合渐进损伤分析方法，建立材料失效准则，并通过对有限单元中材料点的刚度进行折减，预测复合材料损伤演化的过程。

1 复合材料失效准则及损伤演化规律

纤维增强复合材料单向单层板如图1所示。纤维增强复合材料层合板的力学性能和强度具有显著方向性(纤维方向、横向方向和厚度方向)，因此，复合材料单层板的基本强度指标主要有沿铺层主方向(即纤维方向)的拉伸强度Xt和压缩强度Xc，垂直于铺层主方向的拉伸强度Yt和压缩强度Yc，以及平面内剪切强度S等5个强度指标。

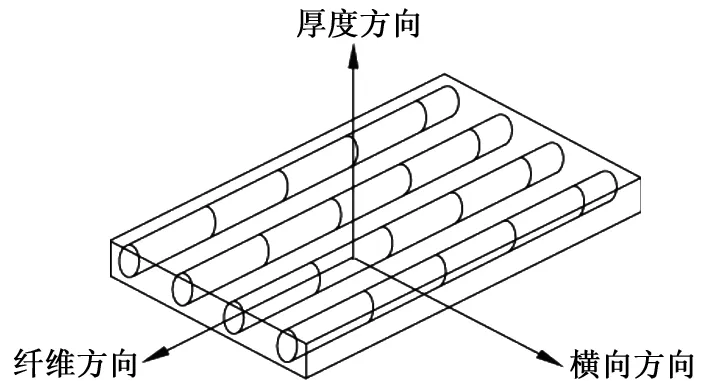
图1 纤维增强复合材料单向单层板

纤维失效准则：

(1)

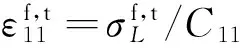
一旦材料点应力/应变状态满足上式，则认为材料点处纤维内出现损伤。定义纤维损伤状态变量df，其损伤演化方程如下：

(2)

基体失效准则：

(3)

一旦材料点应力/应变状态满足上式，则认为材料点处基体内出现损伤[4]。

定义基体损伤状态变量dm，其损伤演化方程如下：

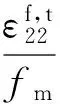
(4)

式中，Gm是基体的断裂能。

在材料渐进失效损伤不断累积过程中，材料承载性能不断退化，体现为材料刚度不断下降，考虑材料损伤的刚度矩阵Cd表示为：

(5)

式中，sym代表矩阵Cd关于对角线的对称部分。

材料的刚度按损伤演化方程折减并更新，实现损伤过程的模拟，当损伤达到临界值，材料点失效。

2 界面失效准则及损伤演化规律

为了考虑复合材料层间力学行为对层合板力学性能的影响，以及下节中胶层界面损伤对胶接修补结构力学性能的影响，在复合材料层间和补片与金属板之间建立界面单元，这些界面单元的力学性能由Traction-Separation本构模型来描述[5]。三维界面单元存在3个应力分量(tn,ts, tt)和3个位移分量(δn,δs,δt)，应力和位移存在一定的对应关系。损伤出现前应力和位移存在线性关系，则其线弹性行为可由下式表示：

(6)

式中，K是刚度系数；Knn、Kss和Ktt是3个方向的刚度系数；δ是应变。

当界面的应力达到损伤初始准则后，损伤萌生，界面的应力和位移关系不再保持原有线性变化，本文中失效准则采用二次应力准则。

(7)

当损伤出现后，界面的应力和位移关系为：

(8)

式中，D是界面的损伤变量，其范围为[0,1]。其表达式如下：

(9)

式中，δ0是初始损伤变量；δmax是最大损伤变量。当D=0时，界面的力学性能为线弹性；当D=1时，界面失效，不再承受传递载荷。

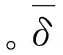
图2 拉伸牵引失效规律

本文采用基于能量的损伤演化规律：

(10)

3 算例验证及分析

通过渐进损伤分析，可以清楚地了解承载复合材料层合板内部损伤的产生及扩展过程。为了验证所建立的复合材料层合板渐进损伤分析模型的有效性，以ABAQUS6.10有限元软件为平台，编写用户材料子程序(UMAT)，建立考虑层内材料点纤维本构模型， 实现复合材料层合板的失效判断及基于损

图3 含中心裂纹的复合材料层合板

图4 有限元模型和边界条件

伤变量材料点刚度连续退化算法。试验采用T800/3900-2含有中心贯穿裂纹的复合材料层合板，铺层方案为[45/0/-45/0/90]s，试件形状和尺寸如图3所示，边界条件及有限元网格如图4所示，单层板力学性能见表1。

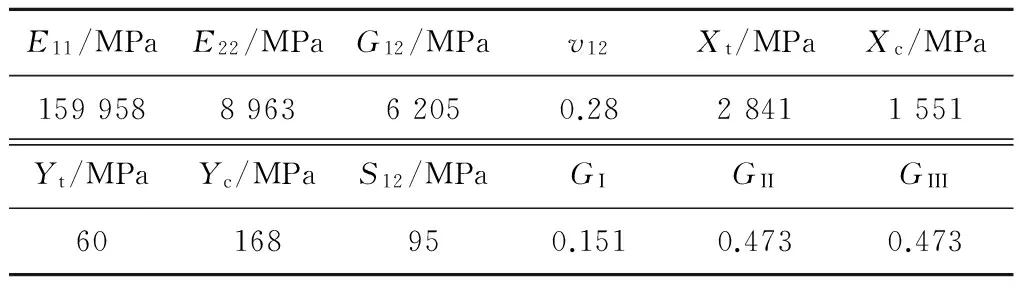
表1 T800/3900-2材料属性

含有中心贯穿裂纹的复合材料层合板载荷—位移曲线如图5所示。图5反映了含中心贯穿裂纹层合板承载过程中材料损伤累积造成的非线性响应，模拟了复合材料层合板试件的拉伸极限强度和损伤破坏过程，与文献[6-7]中的结果较好吻合。

图5 试验和数值计算载荷—位移曲线

含中心穿透裂纹层合板在准静态拉伸载荷作用下层内损伤模式的失效扩展路径见表2。每一层都出现了纤维和基体的损伤，并且层间伴随出现了分层现象。

1)层合板中相同方向铺层的损伤分布相似，其中45°铺层与-45°铺层损伤形式对称。

2)纤维的失效主要发生在0°铺层，然后迅速扩展到45°铺层，纤维断裂沿载荷垂直方向扩展到板自由边界(向板边缘扩展)，最后层合板整体失效。0°方向铺层的纤维失效主要集中在载荷垂直方向上很窄的范围内，只有在最后阶段较大失效面积出现在板边缘。

3)基体失效首先发生在90°铺层，然后迅速扩展到45°铺层和0°铺层，层合板的基体失效面积比纤维失效面积大很多。

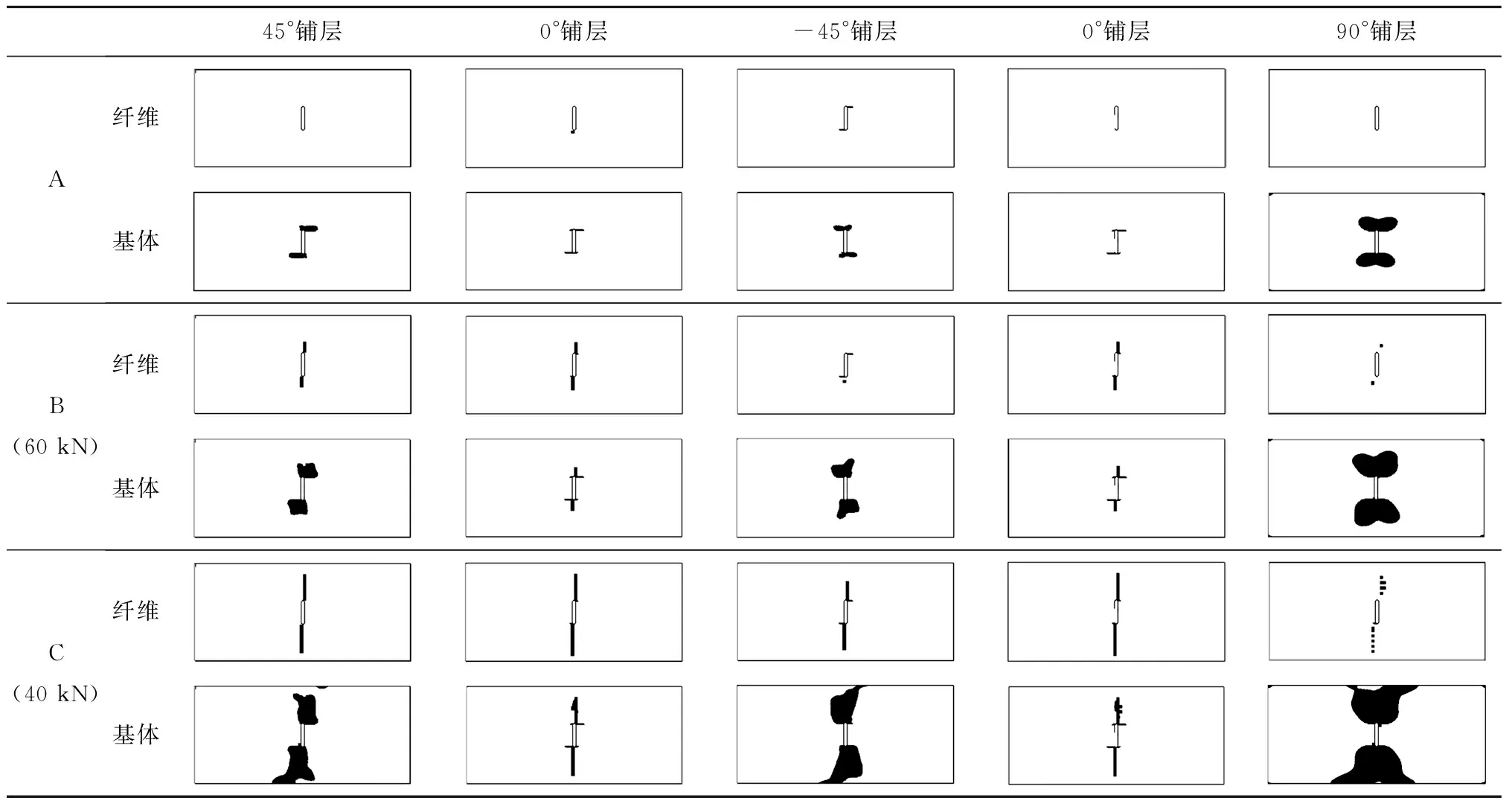
表2 含中心裂纹层合板损伤演化过程

4 结语

复合材料层合板在外载作用下的强度破坏过程是一个逐渐破坏的过程。利用复合材料累积损伤分析方法，建立了复合材料渐进损伤分析非线性有限元模型，考虑基体损伤，纤维损伤和分层3种失效模式，结合混合失效准则以及刚度性能退化方案，模拟出承载层合板内部发生损伤之后载荷的重新分布和损伤的相互作用及扩展过程，并准确预测层合板的局部和整体变形以及最终破坏载荷。

[1] Kumar A M, Hakeem S A. Optimum design of symmetric composite patch repair to centre cracked metallic sheet[J]. Composite Structures, 2000, 49(2): 285-292.

[2] 徐建新. 损伤金属结构的复合材料胶接修理技术研究[D]. 南京:南京航空航天大学,1996.

[3] 郝建滨，穆志韬，李旭东. 金属损伤复合材料胶接修补技术的国内研究现状[J]. 新技术新工艺，2014(11)：122-125.

[4] Kaye R, Heller M. Finite element-based three-dimensional stress analysis of composite bonded repairs to metallic aircraft structure[J]. International Journal of Adhesion and Adhesives, 2006, 26: 261-273.

[5] 王跃全, 童明波, 朱书华. 三维复合材料层合板渐进损伤非线性分析模型[J].复合材料学报, 2009, 26(5): 160-166.

[6] Satyanarayana A, Bogert P B, Chunchu P B. The effect of delamination on damage path and failure load prediction for notched composite laminates[C]//48th AIAA/ASME/ASCE/AHS/ASC Structure, Structureal Dynamics, and Materials Conference. Hampton: NASA Langley Research Center, 2007：1-16.

[7] Bogert P B, Satyanarayana A, Chunchu P B. Comparison of damage path predictions for composite laminates by explicit and standard finite element analysis tools[C]//47th AIAA/ASME/ASCE/AHS/ASC Structure, Structureal Dynamics, and Materials Conference. Hampton: NASA Langley Research Center, 2006: 1-27.

责任编辑郑练

NonlinearProgressiveFailureAnalysisofCompositeLaminate

XU Yuzhen

(Unit 91049 of the Chinese People’s Liberation Army, Qingdao 266102, China)

Because of the big strength, high stiffness and good security properties, composite material is widely used in aerospace field. Studying the damage process of composite materials and its failure pattern has very important engineering value. By means of a progressive damage analysis (PDA) finite element numerical model, composite laminates with central transverse crack are applied to simulate the damage evolution based on reduction with the finite element stiffness of the material points. Failure mechanism is developed to predict the initiation and evolution of damage and ultimate strength clearly. Good correlation with experimental results is achieved both in terms of load-displacement history and the predicted failure mechanisms by comparations between the experimental and numerical results.

composite material, progressive damage, failure analysis, finite element analysis

TB 33

:A

胥玉震(1979-)，男，工程师，主要从事特种设备维修等方面的研究。

2015-03-06