概念教学应重视思维训练的实效性

数学是思维活动的过程，数学教学就是数学思维活动的教学.在概念教学中要以学生为主体，遵循认知规律，以学生现有认知结构为基础，在教学各个环节的设计与实施中，重视学生思维过程（细节）的暴露与训练，进而提高思维训练的实效性.本文拟以“对数”教学中的一些环节来分析思维训练的实效性.

1 概念建构的思维起点应指向学生认知实情

我们知道，“先行组织者”的教学策略对新概念的学习有定向和引导的功能，而“先行组织者”的选取由学生群体的认知水平、认知结构和认知需求共同决定，不同学生群体对同一“组织者”作出的认知反应体现出较大差异，因此，为了切合学生的认知实情，应认真分析学生已有认知结构，选出真正适合学生概念建构的“先行组织者”.

讨论1 “对数”概念引入方式与学情切合分析

常见于课堂中的“对数”引入方式有：

方式1 由已学“指数函数”中的例题引入：

某种放射性物质不断变化为其他物质，每经过1年，这种物质剩留的质量是原来的84%，那么经过x年后，该物质的剩留量y=0.84x，

问1：经过10年，这种物质的剩留量是多少？

问2：经过多少年，这种物质的剩留量为原来的一半？

以求解方程“0.84x=12”引出概念.

方式2 以代数式“ab=N”为载体，从不同角度设计运算：

运算1：若a=2，b=4，则N=    ;

运算2：若b=2，N=4，则a=    ;

运算31：若a=2，N=8，则b=    ;

运算32：若a=2，N=5，则b=    .（引导性问题：b存在吗？如何表示？）

先回顾“根式运算”的过程，再据此类比，引出“对数”.

显然，两种引入方式均能以学生已有认知结构中的素材为研究起点，并且都有共同的目标指向：引入“对数”的必要！通过实践比较，两种引入方式实效大不相同：

方式1从学生刚学过的指数函数中的实际问题入手，研究对象熟悉（指数形式），研究问题清晰（解方程问题），且其中渗透了函数与方程的思想，为后续学习打下基础.但由于此情境为实际问题，学生仍会花时间对此进行建模，更何况从实际问题抽象出函数模型本身就有一定难度，可能因此冲淡主题.所以，该引入方式适用于指数及指数函数学习到位且建模能力较强的学生群体.

方式2是基于从不同角度（三种运算）看同一对象（“ab=N”）的视角而展开的，学生在初中幂运算、根式运算的基础上，通过类比“根式运算”的思维过程，同化到“对数运算”，学习过程具有指向性与探究性.但要求学生对数学对象的表征能力较强，而且“范式”的思维方式要求较高——若在代数式ab=N的不同表征时就出现思维混乱，或在“根式运算”思维过程的“回顾”阶段就出现“卡壳”，便直接影响了“对数运算”相应的思维建构.因此，该引入方式适用于对数学符号表征能力较强且思维品质较好的学生群体.

2 组织方式中的思维价值应致力学生的发展

建构主义理论的核心价值是学生对所学知识的有意义建构，著名心理学家惠特海默认为，不能用无意义的方式来进行有意义的建构.这就表明组织方式将直接影响学生在知识建构中的有效思维含量（思维方式是否进步;思维水平是否提升;思维品质是否优化等等），不同的组织方式最终的教学功能有明显差异，或许在短期内学生都能进行解题，但从学生的长期发展来看，数学观念、数学素养的差异将凸显出来.

讨论2 “对数运算法则”两种组织方式对思维训练的有效成分

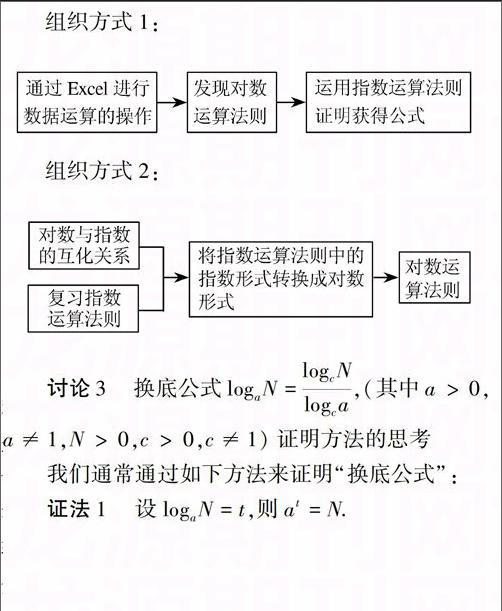
组织方式1：

组织方式2：

具体而言，组织方式1目标明确，指向清楚，更利于探究活动的开展，它遵循从特殊到一般的探索过程，旨在帮助学生建立起“观察—归纳（猜想）—证明”数学探究过程，从而形成正确的科学探索方法.但方式1中“对数运算法则”的发现过程是通过辅助媒介的外部操作获得，学生主体的思维建构成分较少，从有效思维角度来看，辅助媒介代替了学生认知结构中的思维建构，其中的思维训练属于低层次的思维操作，对处于高中阶段的学生的思维发展是不利的.组织方式2中的探究是以学生已有认知为思维起点，探索动机是从已学的“指数化对数”这一基本运算切入，将原有认知系统中“指数运算法则”进行“改装”，这样的思维过程是与之前“对数概念”的形成保持一致，既巩固了原有概念，又进一步诠释了“指数化对数”的内涵，思维过程更趋一致性，更易于学生深刻牢固掌握“对数概念”的本质，且知识的生成过程为有方向引领的思维过程，这显然是帮助学生形成理性思维的良好载体.

3 数学应用的设计应保持思维训练的连续性

数学例题的设计往往是为了巩固概念的理解，加深概念建构中的思想方法的训练，但很多例题的设计却忽视“巩固”的功能，反而节外生枝产生新的认知难点，导致学生头脑中刚建构起的思维链掺入“杂质”，使学生思维混乱，影响了思维训练的连续性.

讨论3 换底公式logaN=logcNlogca，（其中a>0，a≠1，N>0，c>0，c≠1）证明方法的思考

我们通常通过如下方法来证明“换底公式”：

证法1 设logaN=t，则at=N.

两边取以c为底的对数，得logcat=logcN，

tlogca=logcN，

因为logca≠0，所以t=logcNlogca，故logaN=logcNlogca.

从实际教学来看，上述证明中的“两边取对数”这一方法来得很“突然”，学生理解起来很吃力，这是因为学生对“两边同时取同底的对数”这一方法完全没有相应的知识支撑和心理准备，与学生已学的认知方式（即“对数指数的互化”）之间有较大差异，自然接受起来比较生硬.

实际上，从一开始的对数概念到对数运算法则，都经历了“对数式化回指数式”的思维过程，为了“延续”这一思维程式，同样地，我们可以尝试这样证明换底公式：

证法2 设logaN=p，logca=q，则ap=N，cq=a，

于是N=（cq）p=cpq，所以pq=logcN，即logaN·logca=logcN，

由于logca≠0，所以logaN=logcNlogca.

可以看出，证法2立足于指数运算性质（ap）q=apq（a>0），通过指数与对数间的互化而完成.值得说明的是，该证法是建立在已发现“换底公式”的前提下，如果没有这样的知识作为载体，那么对刚学习“对数”的学生来讲，这种方法同样来得很突兀，听起来也并非自然流畅.

证法3 设logaN=t，则at=N，由恒等式a=clogca，则N=（clogca）t=ctlogca，

由对数的意义，得tlogca=logcN，

由于logca≠0，所以t=logcNlogca，即logaN=logcNlogca.

证法3立足于对数恒等式a=clogca（c>0，c≠1，a>0），通过指数对数的互化得以完成，用到的知识和思维方式与之前的保持连续性，学生接受起来可能要好得多.

所以，在数学应用的过程中，我们要认真审视教学内容与学生原有认知在思维方式上的联系，尽可能地保持思维的连续性，强化知识的本质理解.

作者简介 丁益民，男，江苏姜堰人，1981年出生，中学一级教师，全国新青年数学工作室核心成员，主要从事高中数学教育和初等数学研究工作，近年来在省级以上期刊上发表论文80多篇，多篇文章被人大复印资料全文转载.