浅谈夯实基础培养学生的数学素质

吴灵喜

（浙江省兰溪第三中学）

圆锥曲线在数学上是一个非常重要的几何模型，有很多几何性质，这些重要的几何性质在日常生活、社会生产及其他科学中都有着重要而广泛的应用，并且学习这部分内容对于提高自身的素质是非常重要的.其中抛物线是圆锥曲线中的重要的一类，在高考中有着重要的地位.特别地，在导数引入高中数学，对抛物线的考查就更为频繁.在学习了抛物线的定义以及抛物线的几何性质之后，为了更好地理解抛物线的定义，笔者从下面几个方面进行说明.

一、巩固抛物线的定义

1.到点A（1，1）的距离与到直线l:3x-4y+1=0 的距离相等的点的轨迹是 （ ）

A.椭圆 B.双曲线 C.抛物线 D.直线

解析：粗看满足抛物线的定义，再仔细一看，易发现点A∈l，点的轨迹为经过点A 且垂直于直线l 的一条直线. 这有助于理解抛物线的定义——直线外的一点.

2.经过点F（2，0）且与直线l:x=-2 相切的动圆的圆心M 的轨迹是 （ ）

A.椭圆 B.双曲线 C.抛物线 D.直线

解析：由圆的性质及直线与圆相切的性质可知，圆心到切线的距离等于半径，又点F 在圆M 上：即圆心M 到定点F 的距离等于到定直线l 的距离，满足抛物线的定义，所以动圆心M 的轨迹是抛物线.

变式1：到点F（2，0）的距离比到直线l:x=-1 的距离大1 的点的轨迹是 （ ）

A.圆 B.椭圆 C.双曲线 D.抛物线

解析：把直线l 向左平移一个单位，可以转化为l′∶x=-2，到定点F（2，0）的距离等于到定直线l′:x=-2 的距离，满足抛物线的定义。

轨迹为 （ ）

A.圆 B.椭圆 C.双曲线 D.抛物线

解析：等式可化为：

根据两点间的距离和点到直线的距离公式可得，动点M（x，y）到定点F（2，0）的距离等于到定直线l:3x+4y-2=0 的距离，满足抛物线的定义（不是我们所熟悉的标准条件下的抛物线）.

二、抛物线定义的简单应用

1.求焦点在x 轴上，且抛物线上一点A（3，m）到焦点的距离为5 的抛物线的标准方程.

解析：根据题意，设抛物线的标准方程为：y2=2px（p>0），如果运用两点间距离公式，待定系数法联立方程组解得，运算量较大.所以可根据抛物线的定义，抛物线上的点A 到准线：x=-p/2 的距离等于5，可得到p 的值，从而求得抛物线的方程.

2.已知抛物线y2=2x 的焦点是F，点P 在抛物线上，有一定点A（3，2），求｜PA｜+｜PF｜的最小值，及对应的点P 的坐标.

解析：由定义可知，抛物线上的点P 到焦点F 的距离等于点P到准线l 的距离d，所以求｜PA｜+｜PF｜的最小值，转化为求｜PA｜+d 的最小值，由点与直线上的点的连线中垂线段最短可得，过点A 作准线的垂线，垂线段长即为所求的最小值，该垂线与抛物线的交点就是所求的点P.

变式：已知抛物线y2=2x 的焦点是F，点P 在抛物线上，有一定点A（2，3），点P 到y 轴的距离为d，求｜PA｜+d 的最小值.

解析：P 到y 轴的距离，可以延长到准线的距离，再根据抛物线的定义，转化为到焦点的距离，即（｜AP｜+｜PF｜）-1/2 的最小值，当A、P、F 三点共线时取最小值.

3.已知抛物线y2=2px（p>0）的焦点是F，准线为l，过点F 的弦AB 为直径的圆与准线l 的位置关系 .

解析：过点A，B 分别作准线l 的垂线，垂足分别是A1，B1，取AB 的中点为C，过C 作准线l 的垂线，垂足为C1，由抛物线的定义可知：｜BB1｜=｜BF｜，｜FA｜=｜AA1｜.

∴｜AB｜=｜AA1｜+｜BB1｜.

∵CC1是梯形ABB1A1的中位线.

∴2｜CC1｜=｜AA1｜+｜BB1｜.

∴｜AB｜=2｜CC1｜，即圆心C 到准线的距离等于半径.

∴以AB 为直径的圆与准线l 相切.

变式：已知抛物线y2=2px（p>0）的焦点是F，准线为l，过点F的弦AB，作AA1⊥l，BB1⊥l，垂足为A1，B1，求证：A1F⊥B1F.

解析：在△AA1F 和△BB1F 中，根据抛物线的定义可知，｜AF｜=｜AA1｜，｜BF｜=｜BB1｜，

∴2∠A1FA+∠A1AF=180°，

2∠B1FB+∠B1BF=180°，AA1∥BB1，

∴∠A1AF+∠B1BF=180°，

∴∠A1FA+∠B1FB=90°，

∴∠A1FB1=90°，即A1F⊥B1F.

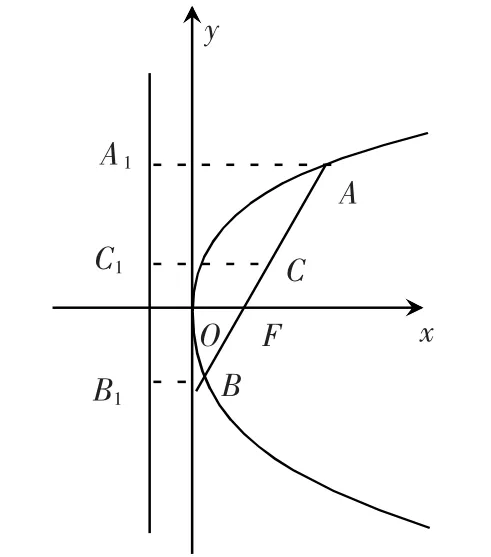
4.已知AB 是抛物线y=x2上的动弦，且｜AB｜=a（a 为常数且a>1），求弦AB 的中点M 的纵坐标的最小值.

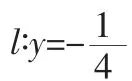
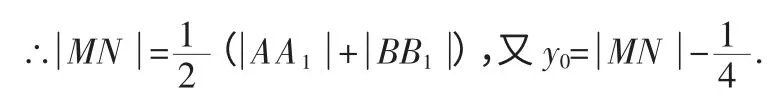
连接AF，BF，在△ABF 中，｜AF｜+｜BF｜≥｜AB｜=a，当且仅当AB 经过焦点F 时取“=”.

根据抛物线的定义可知：｜AA1｜=｜AF｜，｜BB1｜=｜BF｜，

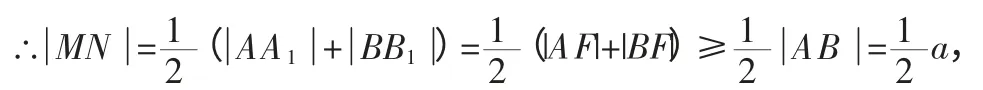
5.如下图，过抛物线y2=2px（p>0）的焦点F 的直线l 交抛物线于点A、B，交其准线于点C，若｜BC｜=2｜BF｜，且｜AF｜=3，则此抛物线的方程是（ ）

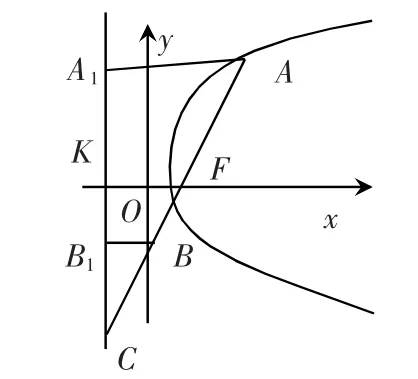
解析：过A，B 分别作准线的垂线，垂足为A1，B1，准线与x 轴相交于点K，则｜BF｜=｜BB1｜.

∵｜BC｜=2｜BF｜，∴｜CB｜=2｜BB1｜，∴∠B1CB=30°，

∴｜AC｜=2｜A1A｜=2｜AF｜=6，

∴F 为AC 的中点.

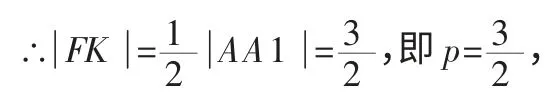
∴抛物线的方程为y2=3x.

通过以上几个例子，让我们能够进一步理解抛物线的定义，能更好地解决与抛物线有关的焦半径问题和焦点弦问题，解决有关抛物线的最值问题和定点、定值问题.重视概念的理解是掌握基础知识的第一步，是发展学生基本技能，培养学生的运算能力、思维能力、逻辑推理能力和分析解决问题的能力的基础，是培养学生数学素养的基础.

任志鸿.高中同步测控优化训练：数学［M］.人民教育出版社，2012-09.