基于加权交叉耦合的多电机同步控制研究

谷雨，马钺

（1.中国科学院沈阳自动化研究所，辽宁沈阳110016；2.中国科学院大学，北京100049）

现代生产制造业中，无论在高精度加工领域，还是传统产品生产线中，多电机同步系统已经得到了越来越多的应用［1］。例如在造纸、轧钢等生产过程中，电机同步效果直接影响了系统生产效率和产品质量［2］。

为实现电机间的协调同步，目前的控制策略主要有：主从控制，并行控制［3］，交叉耦合控制［4］，虚拟总轴控制［5］等。但是，这些控制策略中往往存在着控制精度不高等问题，而且随着电机数目的增加，耦合强度呈指数增加，对整个系统控制愈发复杂［6］。为了简化控制结构，提高可控电机数目，学者们［7-9］通过只考虑相邻电机影响而提出了相邻交叉耦合的控制策略。但是这种控制策略将系统中的电机同等看待，而忽略了电机之间的实际关系。在多电机同步系统中，电机的关系并不相同，重要性也并不一致［10］。对于所有电机采用相同的控制强度，限制了同步控制精度和生产效率。

本文参考了相邻交叉耦合控制策略，考虑电机之间的主次关系，改进电机系统结构，提出了加权交叉耦合的多电机同步控制策略以及相应的控制算法。在文章最后，基于外观质量检测线进行了仿真实验，验证了采用加权交叉耦合控制改进之后，同步控制效果提升明显。

1 加权交叉耦合控制策略

1.1 同步控制策略

在多电机同步系统中，不仅要考虑每台电机自身状态，还要考虑其他电机的影响。在相邻交叉耦合控制［8］中，电机参考相邻2台电机的状态，根据电机间的同步误差补偿控制信号。但是由于电机职能的不同，电机间的影响程度也就不同。如在一条产品质量检测线中，有出入料带电机，离心转盘电机，水平带电机等10 多台电机同时运行。生产过程中，处于检测环节的传动电机，远比出入料电机对于检测结果带来的影响大。如果只考虑相邻电机，无法区分电机间的主次关系，则降低了控制效率。

因此，针对不同电机需要设定不同的权重。设定系统中某台电机的重要程度更高，则该电机可以影响更多电机。这样，当高权重电机出现扰动时，通过系统中大部分电机共同作用，可以达到更快的恢复速度。而当次要电机出现扰动时，只由少数电机来分担误差扰动，简化了控制结构。

1.2 加权交叉耦合的多电机模型

对于n台电机的多电机系统，第i台电机的机械转动方程为［9］

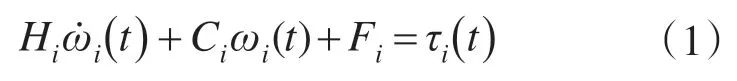
式中：ωi为第i台电机的转速；Hi，Ci分别为转动惯量和非线性参数；Fi为外部扰动；τi为输入转矩。设定转速误差为

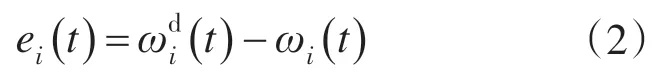
设定2台电机i与j之间的影响关系由aij来表示。当电机之间存在影响关系时，aij=1，否则aij=0。第i 台电机对于系统的重要程度通过其影响的电机数目之和来表示。

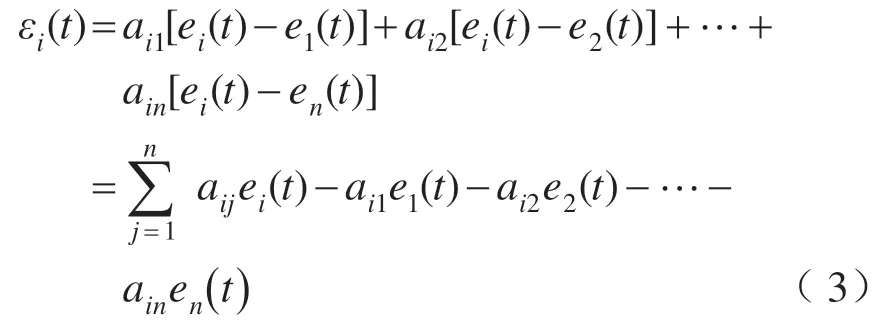
对于n台电机，可将同步误差表示为如下矩阵：

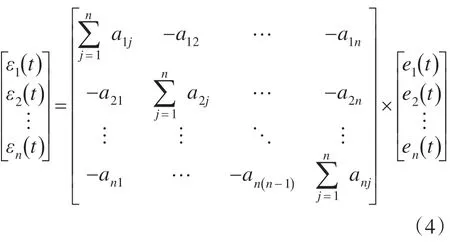
并设：

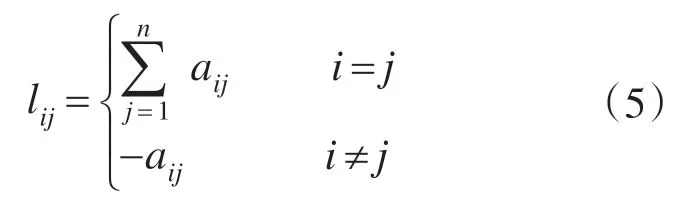
则有：

式中：L为多电机系统的关系矩阵；ε为同步误差矩阵；E 为转速误差矩阵。

由定义可知L 为对称矩阵，且L 的秩为Rank=n-1。

于是，如果能够控制系统使得同步误差ε为零，则有方程LE=0。可以得到方程通解为

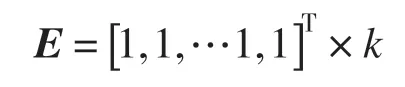
即满足，

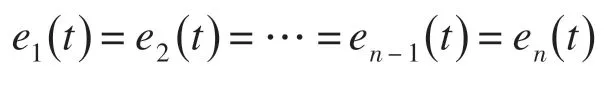
可以保证系统误差同步。

2 控制器设计稳定性分析

2.1 控制器算法设计

若要有效控制多电机系统，则需要控制同步误差以及单台电机误差。设定电机系统的总误差：

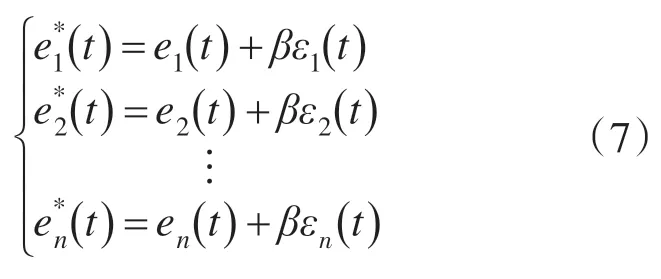
式中：β为正常数。

定义控制量为ui(t)如下：

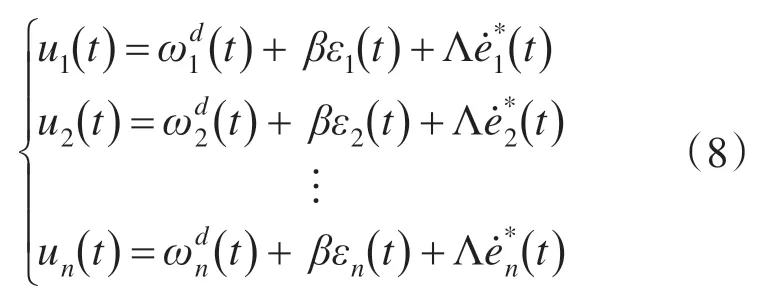
其中，Λ是正常数。并根据ui(t) 定义以下向量：

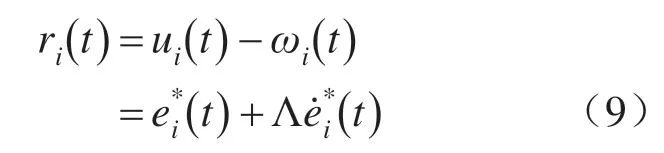
根据滑模控制理论，如果能够控制τi(t)使得ri(t)处于滑动平面上，则系统误差将以指数形式趋于零。

设计控制转矩为

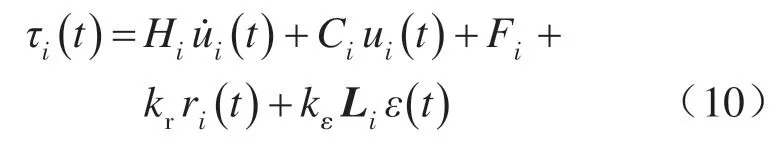
式中：kr，kε均为正控制增益；Li为关系矩阵L第i行行向量。

由式（1）、式（9）和式（10）可以得到关于多电机系统的闭环方程：

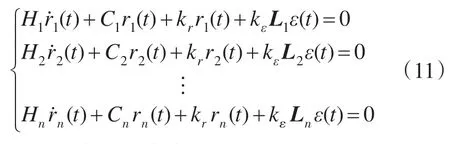
2.2 稳定性及有效性分析

定义李雅普诺夫函数为

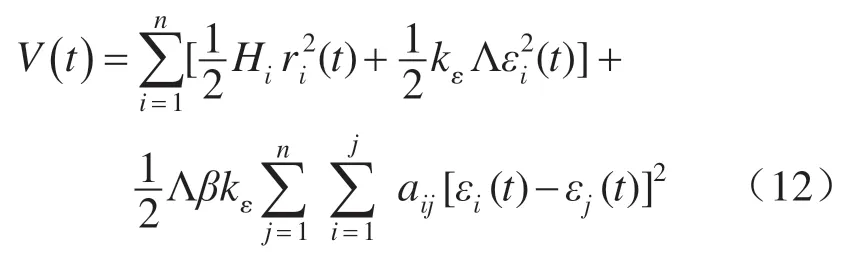
显然，V(t) ≥0。将其对t求导，可得：

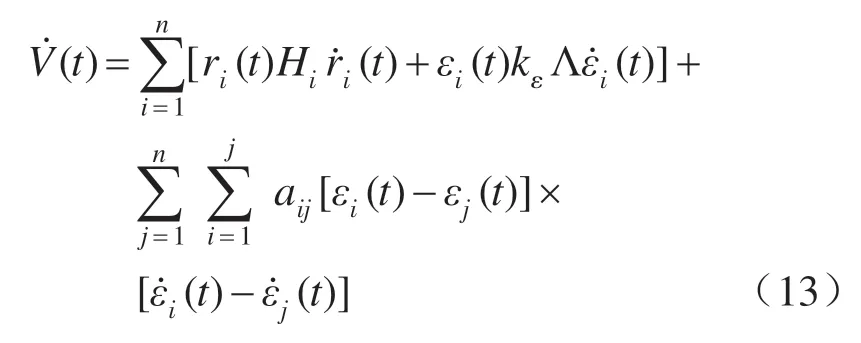
将式（11）左乘以ri(t) ，带入上式得：

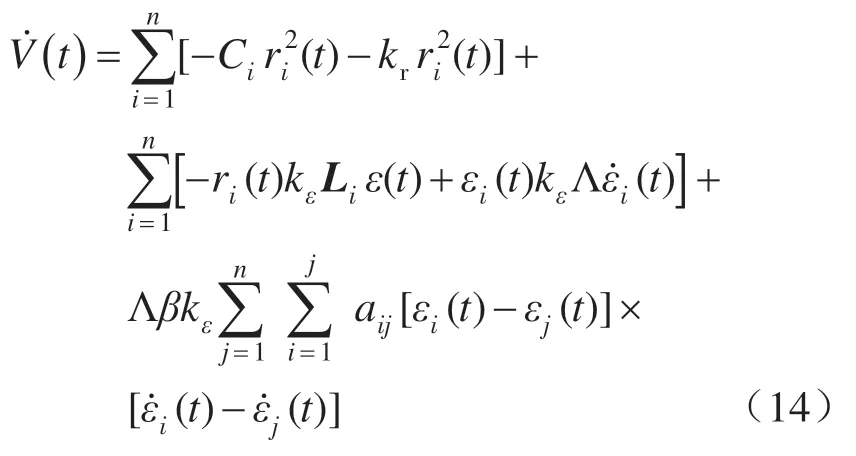
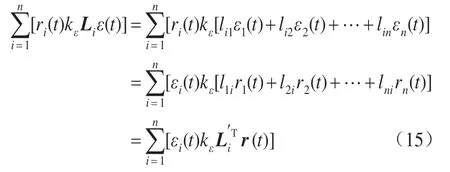
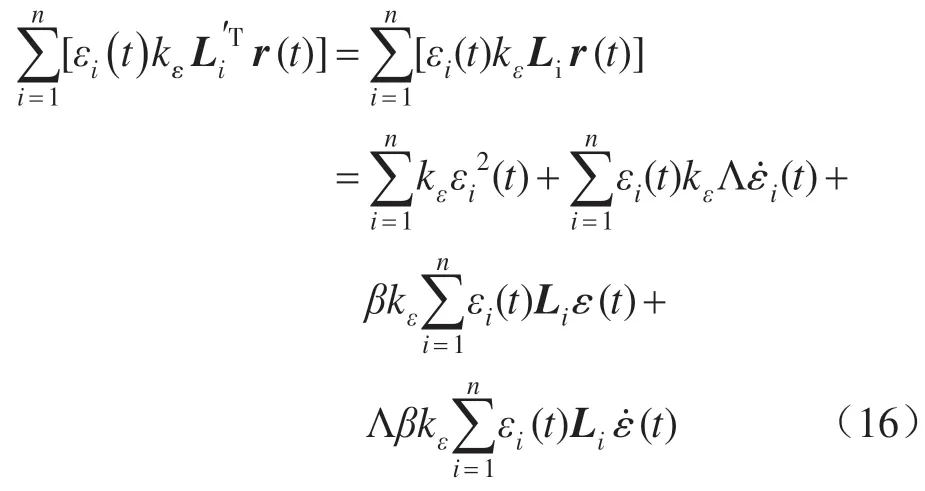
其中

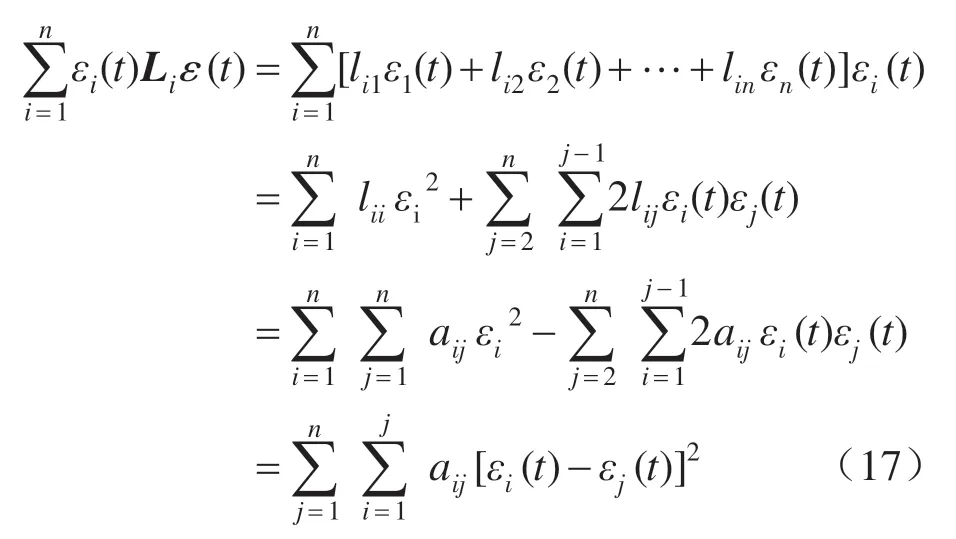
另有

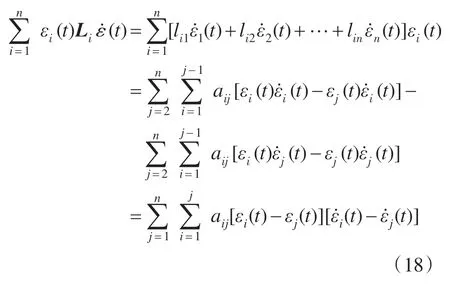
于是有：

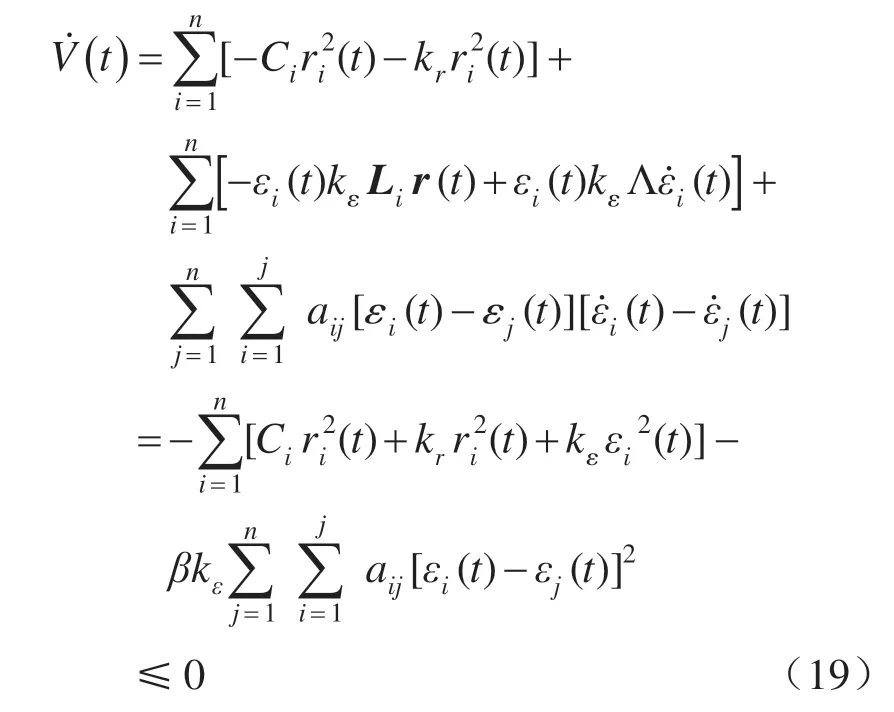
由此可知系统稳定，并由式（7），式（9），式（11），根据Barbalat 定理［12］和LaSall 定理［13］，当t →∞时即系统稳定并且其同步误差和转速误差均将收敛于零。

3 仿真与实验

3.1 仿真实验

现对于上述策略进行Simulink 仿真验证。根据某火腿肠厂在线外观质量检测系统搭建10台交流电机同步系统模型。

按照生产线流程关系：入料电机→提升电机→离心转盘电机→自转电机→水平带电机→水平带电机→调相轮电机→胶辊带电机→自转电机→出料电机，定义电机之间权重比例关系如下：

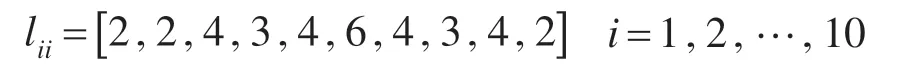
其他电机参数和期望转速参考自系统电机实际参数以及运行情况。

3.2 实验结果与分析

首先选取外观质量检测线中检测水平带电机，针对同步效果进行了仿真实验，并与相邻交叉耦合控制和无同步控制器对比结果如图1、图2所示。

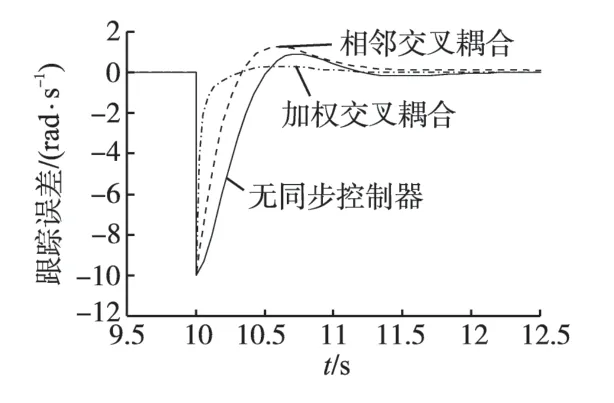
图1 单电机跟踪误差曲线Fig.1 The curves of single motor′s tracking error

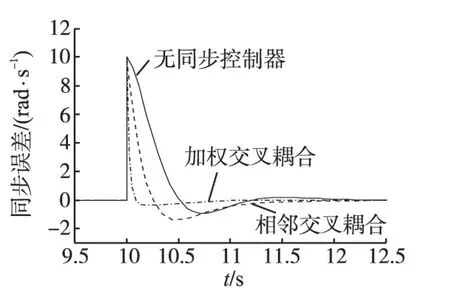
图2 单电机同步误差曲线Fig.2 The curves of single motor′s synchronization error

从图1、图2 可以看出，当系统中出现扰动时，加权交叉耦合控制效果要优于相邻交叉耦合。对比相邻交叉耦合控制，单电机扰动（见图1）调节时间由1.33 s 缩短到0.73 s，超调量也由12.7%减小到3.16%。在同步误差方面（见图2），加权交叉耦合在0.39 s 左右达到最大超调0.3%，控制效果优于相邻交叉耦合。

现对于系统效率改进效果进行仿真实验。系统效率与电机总误差正相关，设定系统加权误差为EW：

当不同权重的电机出现扰动时，针对加权交叉耦合与相邻交叉耦合的系统效率损失情况进行对比实验。选取检测水平带电机（权重6）和提升电机（权重2）进行对比，结果如图3、图4所示。

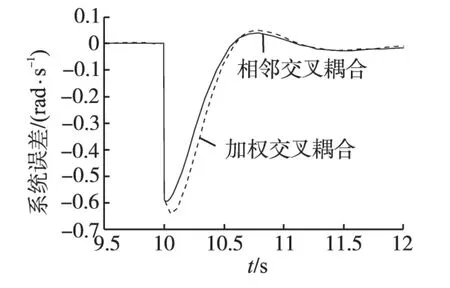
图3 系统加权误差曲线（权重2）Fig.3 The curves of system weighted error（weight=2）

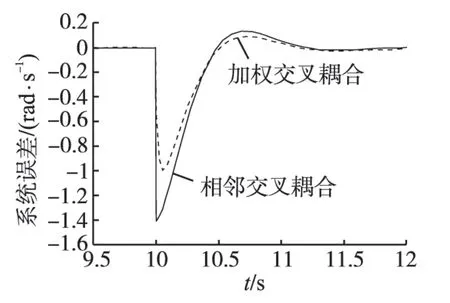
图4 系统加权误差曲线（权重6）Fig.4 The curves of system weighted error（weight=6）

图3、图4 的仿真结果指出，不同职能电机出现扰动时，系统效率损失的确不同，检测水平带电机位于检测系统中心环节，出现负载扰动时，对效率影响更大（见图4）。相邻交叉耦合并没有区分电机的重要程度，当检测水平带电机出现扰动时，系统误差变化较大（EW=6=-1.41），提升电机等权重小的电机的误差变化较小（EW=2=-0.59）。采用加权耦合控制之后，检测水平带的负载扰动对系统误差影响减弱（EW=6=-0.99），而由提升电机的扰动而造成的系统误差并没有太大变化（EW=2=-0.64）。

仿真结果表明，加权交叉耦合能够实现多电机间的协调同步，并且性能优于常规控制策略。

4 结论

本文针对目前的同步控制器中，对于电机无差别处理而导致的同步精度下降问题进行了研究，提出了加权交叉耦合控制策略。该策略对系统中不同权重的电机采取了不同的控制强度。..以此为基础，设计了控制转矩，并通过李雅普诺夫定理证明了闭环系统的稳定性和算法的有效性。仿真结果表明，采用加权交叉耦合控制算法后，多电机系统同步效果得到了有效改善，有助于提升生产效率。

［1］刘福才，张学莲.多级电机传动系统的同步控制理论与应用研究.［J］.控制工程，2002，9（4）：87-97.

［2］陈威，吴益飞，杜仁慧，等.双电机同步驱动伺服系统的鲁棒动态面控制［J］.信息与控制，2013，42（5）：625-631.

［3］彭思齐，戴瑜兴，许海霞.LED 多线切割机自动绕线的并联差分耦合同步控制［J］.信息与控制，2012，41（5）：559-563.

［4］Shih Y T，Chen C S，Lee A C. A Novel Cross-coupling Control Design for Bi-axis Motion.［J］. International Journal of Machine Tool&Manufacture，2002，42（14）：1539-1548.

［5］Anderson R G，Lorenz R. Web Machine Coordinated Motion Control Via Electronic Line-shafting［J］.IEEE Transaction on Industry Applications，2001，37（1）：247-254.

［6］刘然，孙建忠.基于环形耦合策略的多电机同步控制研究［J］.控制与决策，2011，26（6）：957-960.

［7］Dong Sun. Position Synchronization of Multiple Motion Axes with Adaptive Coupling Control［J］.Automatics，2003，39（6）：997-1005.

［8］张承慧，石庆升，程金.一种基于相邻耦合误差的多电机同步控制策略［J］.中国电机工程学报，2007，27（15）：59-63.

［9］曹玲芝，李春文，牛超，等.基于相邻交叉耦合的多感应电机滑模同步控制［J］.电机与控制学报，2008，12（5）：586-592.

［10］张代林，刘宇晗，杨吉祥，等.基于多层模糊控制的交叉耦合补偿方法的研究及应用.［J］.机械设计，2012，29（1）：36-39.

［11］LaSalle J P. The Stability of Dynamical Systems［M］. SIAM Publications，Philadelphia，1976.

［12］Hartmut，Logemann，Eugene P R. Asymptotic Behavior of Nonlinear Systems［J］. The American Mathematical Monthly，2004，111（10）：864-889.