基于改进模型预测控制的永磁同步电机DTC方法

雷亚洲，徐艳平，周钦

（西安理工大学电气工程系，陕西西安710048）

模型预测控制（MPC）具有便于处理复杂约束控制问题、参数依赖性小的优点，自20 世纪80年代以来在过程控制领域得到了广泛的应用。然而由于模型预测控制需要在线求解开环最优控制问题，计算量大，而交流调速系统属于快速动态的机电系统，采样周期短，因而模型预测控制在交流调速领域的研究进展并不顺利。随着数字信号处理器（DSP）等控制芯片计算能力的大幅提高，模型预测控制在交流调速领域中的应用成为可能，对模型预测控制在交流调速领域中的研究成了新的研究热点[1-3]。模型预测控制电压矢量的选择方式可以很好地和直接转矩控制（DTC）相结合，其最大的特点在于电压矢量的选择是通过对电机未来状态进行预测优化得到的，选择更加准确，并且模型预测控制的优化判据——价值函数使得在控制目标中加入降低开关频率、最大转矩电流比等各种非线性约束变得更加方便灵活[4]。

模型预测控制分为两类：连续控制集模型预测控制（CCS-MPC）和有限控制集模型预测控制（FCS-MPC）[5]。其中有限控制集模型预测控制可以将逆变器的离散开关状态与控制目标结合起来，且原理简单，易于实现[4，6-8]。对于两电平逆变器驱动的永磁同步电机调速系统，传统有限控制集模型预测控制需要根据7种不同作用的电压矢量对电流和磁链分别进行7 次预测，并经过7次价值函数计算后选择出使价值函数最小的最佳电压矢量，因此计算量较大，不利于在永磁同步电机调速这种快速动态系统中实现。为减少计算量，通常是在预测之前根据最小开关切换原则筛选出部分待选矢量[4]。由于这种方法在基本电压矢量的某个子集中寻找最优电压矢量，因而不能保证在任何时刻都能选择出全局最优的电压矢量，可能会影响到系统的动静态性能。文献［9］针对异步电机有限控制集模型预测控制计算量大的问题，根据电机方程对预测过程进行了简化，使得计算量有了显著的降低，但是针对永磁同步电机有限控制集模型预测控制预测过程进行简化的研究未见报道。

本文深入分析了永磁同步电机定子电流和定子磁链的关系，提出了一种无需定子电流预测，只需对定子磁链进行预测的基于改进模型预测控制的直接转矩控制方法，使得计算量和算法复杂度得到了显著的降低。实验结果证明了该方法的可行性和在减小转矩脉动、降低计算量上的有效性。

1 永磁同步电机离散数学模型

以定子电流is和定子磁链Ψs为状态变量，永磁同步电机在两相静止（α-β）坐标系下的状态方程为

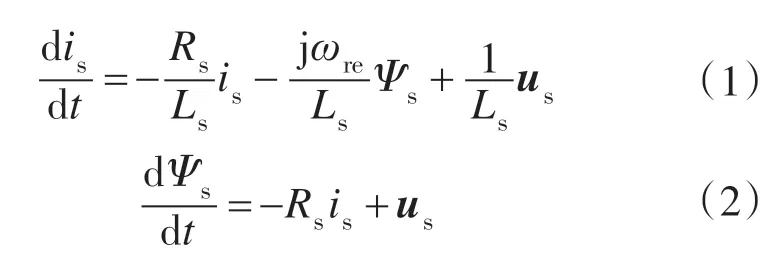
式中：Rs为定子电阻；Ls为定子电感；ωre为转子电角速度；us为定子电压矢量。

永磁同步电机的转矩方程为

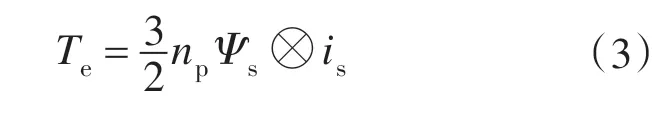
式中：Te为电磁转矩；np为极对数；⊗为叉乘。

采用一阶欧拉离散法将式（1）、式（2）离散化可得

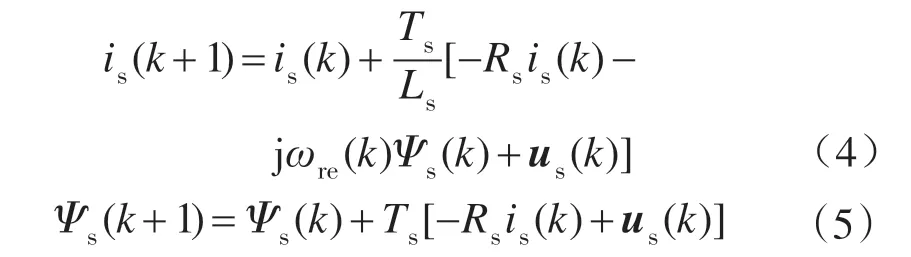
式中：Ts为采样周期；is(k)，Ψs(k)分别为当前时刻定子电流和定子磁链状态变量；is(k+1)，Ψs(k+1)分别为下一时刻预测得到的定子电流和定子磁链状态变量。

2 基于改进MPC的DTC方法

根据逆变器的离散本质特性，可利用有限控制集模型预测控制将模型预测控制中的求解最优化问题转变为：评估逆变器所有可产生的有限个电压矢量，并选择其中使得价值函数最小的电压矢量作为下一时刻电机的输入。

2.1 传统模型预测控制

用于直接转矩控制的传统模型预测控制以转矩和定子磁链为控制目标，对每个电压矢量作用下的转矩和磁链进行预测，再根据转矩和磁链误差最小的原则选择出最佳电压矢量作为下一时刻电机的输入。永磁同步电机离散数学模型式（4）和式（5）可分别用来预测定子电流is(k+1)和定子磁链Ψs(k+1)，同时根据转矩方程式（3），可得下一时刻的转矩预测值：

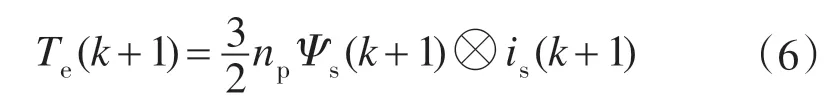
同传统直接转矩控制一样，为了在保持定子磁链幅值恒定的情况下，控制转矩快速跟随指令值，选取价值函数如下：

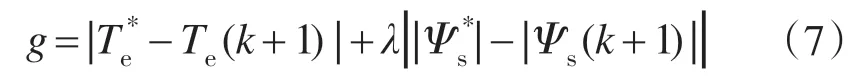
两电平电压型逆变器可以产生6个基本电压矢量和2个零矢量，共7种不同作用的电压矢量，由两电平电压型逆变器驱动的用于永磁同步电机直接转矩控制的传统模型预测控制方法如下：

1）根据离散电机模型式（4）、式（5）预测这7种电压矢量作用后的定子电流和定子磁链，并根据式（6）计算转矩预测值；

2）根据价值函数式（7）计算出7 种电压矢量对应的7个g值；

3）比较7个g值，并选出使得g最小的电压矢量，作为下一时刻电机的输入。

2.2 改进模型预测控制

由于传统模型预测控制需要在一个采样周期内对7 种电压矢量的作用效果进行预测，即需要对定子电流和定子磁链分别计算7 次，同时价值函数也需要计算7 次，其中，电流预测方程式（4）较为复杂，因此，简化式（4）对整体计算量的降低具有至关重要的意义。

将离散磁链状态方程式（5）代入离散电流方程式（4），消除定子电压，得

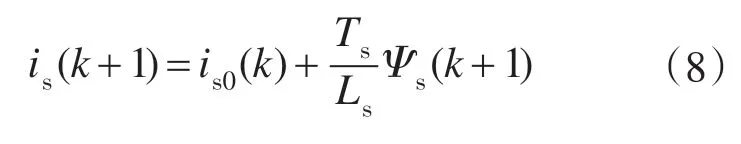
其中

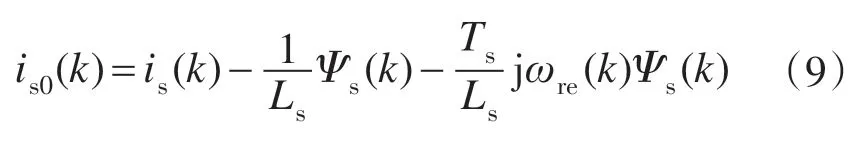
is0(k)仅与k时刻输入及状态量相关。

将式（8）带入式（6），由于Ψs(k+1)⊗Ψs(k+1)=0，得

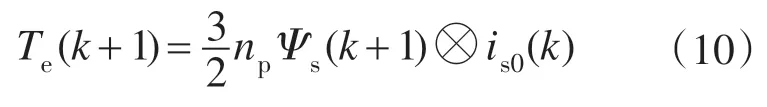
通过式（10）计算转矩预测值Te(k+1)时，仅需对磁链Ψs(k+1)进行预测，而is0(k)只需根据当前时刻的输入和状态量通过式（9）计算1 次即可。与传统模型预测控制相比，改进的模型预测控制省却了计算量最大的定子电流预测，大大降低了算法计算量。

基于改进模型预测控制的永磁同步电机直接转矩控制系统框图如图1所示。

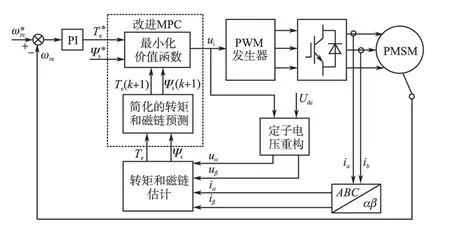
图1 基于改进MPC的永磁同步电机DTC系统框图Fig.1 Block diagram of PMSM DTC based on improved MPC

3 实验结果及分析

为了验证所提出的基于改进模型预测控制的永磁同步电机直接转矩控制方法，简称改进MPC-DTC，针对PMSM 在基于TMS320F28335 DSP实验平台上进行了验证。实验中用到的PMSM参数为永磁体磁链0.24 Wb，定子电感8.5 mH，额定电压200 V，额定电流9.4 A，定子电阻0.2 Ω，额定转速2 000 r/min，极对数4，转子惯量0.001 2 kg·m2。

为了能更好地说明所提出方法的优点，在同一实验平台上也进行了永磁同步电机传统直接转矩控制和基于传统模型预测控制的直接转矩控制的实验。实验中，3 种控制方法的采样频率均为10 kHz。传统DTC 磁链滞环宽度为0.001 Wb，转矩滞环宽度为0.02 N·m；传统MPC-DTC和改进MPC-DTC 权重系数均为53。算法计算所需的时间由DSP的I/O口输出高低电平至示波器测量得到，其余所有波形均由扩展的4通道D/A转换芯片输出到示波器上采集得到。实验结果如图2～图4所示。

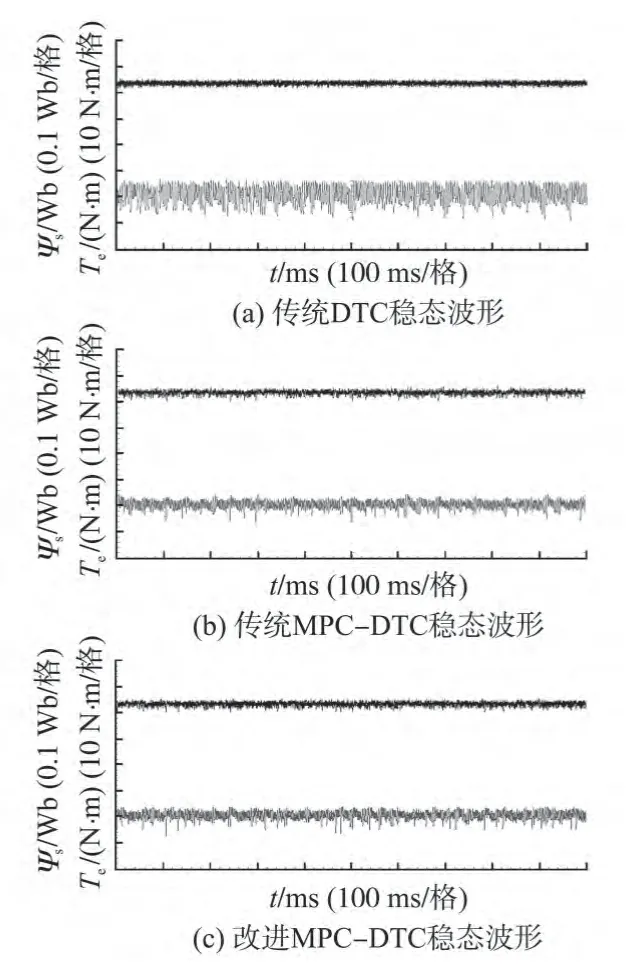
图2 3种控制方法的稳态实验波形Fig.2 Experiment results of three strategies at steady-state

图2为传统DTC、传统MPC-DTC 和改进MPC-DTC控制下的电机空载运行于1 000 r/min时的磁链和转矩稳态实验波形。从图2 可以看出，3 种控制方式下的磁链都稳定地运行在给定值0.24 Wb。转矩性能方面，传统DTC 方式下的转矩脉动约为6 N·m，传统MPC-DTC方式下的转矩脉动约为3 N·m，改进MPC-DTC 方式下的转矩脉动约为3 N·m，说明传统MPC-DTC 和改进MPC-DTC 均可减小转矩脉动，且改进MPC-DTC 具有和传统MPC-DTC 相同的稳态性能。

图3是电机给定转速为1 000 r/min空载启动时，传统DTC、传统MPC-DTC和改进MPC-DTC控制方式下的转速和转矩实验波形。从图3可以看出，当电机给定转速为1 000 r/min 时，改进MPC-DTC 约需0.09 s 达到给定转速，而传统DTC和传统MPC-DTC同样约为0.09 s。并且在转速变化的过程中，3 种控制方法下的转矩也都迅速响应了转速的变化。从图3 可以看出改进MPC-DTC 方法具有与传统DTC 和传统MPC-DTC相同的转速响应速度。

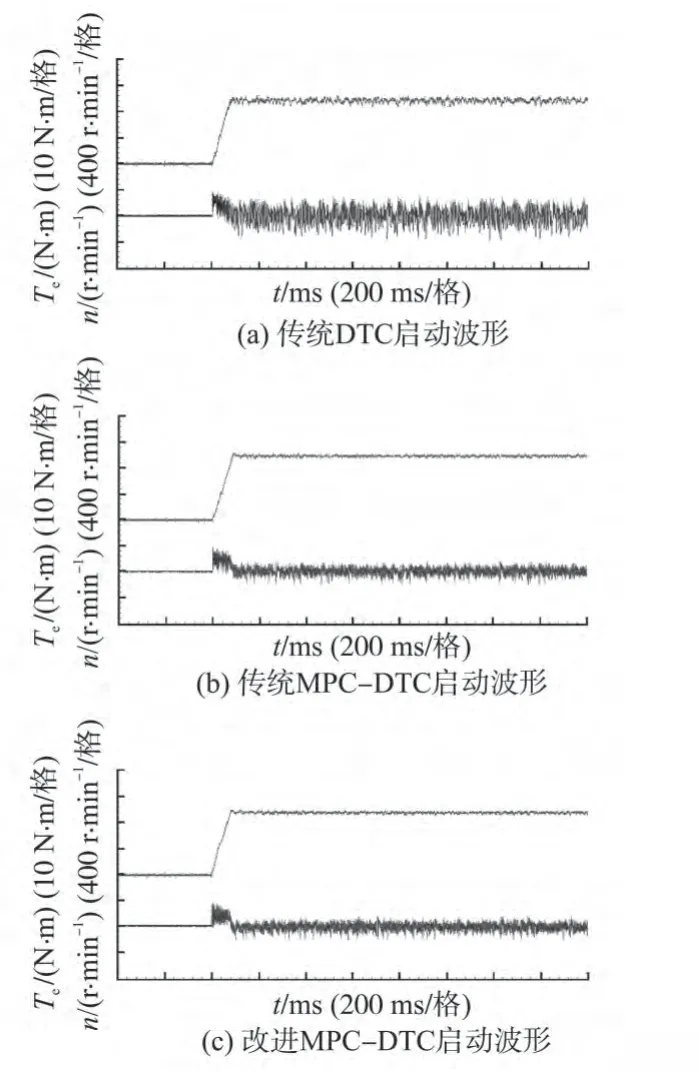
图3 3种控制方法的启动实验波形Fig.3 Experiment results of three strategies at start-up

图4是电机带负载2 N·m 稳定运行于800 r/min 时突减负载至0 时的传统DTC、传统MPC-DTC 和改进MPC-DTC 方式下转速和转矩实验波形。从图4 可以看出，3 种控制方法下系统带载均可稳定运行在800 r/min，当负载突减至0 时转速经过微小波动后仍然可以稳定运行在800 r/min。当负载突减至0 时，改进MPC-DTC 转矩响应时间约为0.08 s，而传统DTC和传统MPC-DTC同样约为0.08 s。这说明采用改进MPC-DTC 控制方法后，系统仍然具有与传统DTC 和传统MPC-DTC 相同迅速的转矩响应。

表1 是传统MPC-DTC 和改进MPC-DTC 算法计算所需时间对比结果。从表1可以看出传统MPC-DTC 计算所需时间为46 μs，而改进MPC-DTC 所需时间仅为28 μs，改进MPC-DTC计算量较传统MPC-DTC减少了近40%。

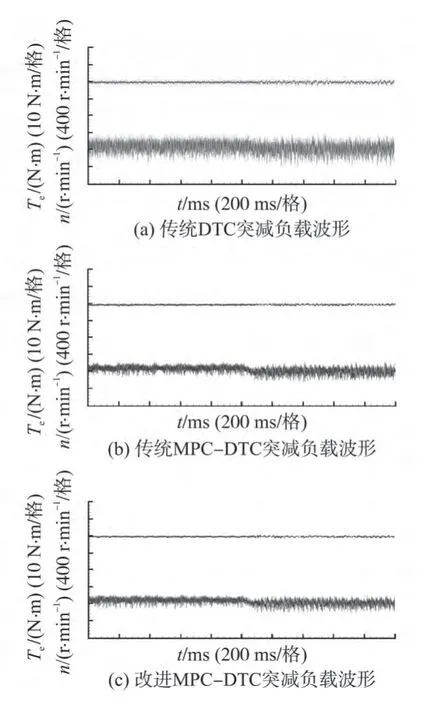
图4 3种控制方法的突减负载实验波形Fig.4 Experiment results of three strategies under changed torque

表1 计算量对比Tab.1 Comparision of calculation amount

从上述实验结果可以看出，改进MPC-DTC方法和传统MPC-DTC 都可以有效地降低转矩脉动，同时改进MPC-DTC 方法仍然具有和传统DTC、传统MPC-DTC 同样迅速的动态响应速度。并且，改进MPC-DTC 方法相较于传统MPC-DTC 在计算量上有了显著的降低，这使得该方法可以在更高采样频率的系统中能够得以实现，进而可以获得更好的控制性能。

4 结论

本文针对永磁同步电机传统模型预测控制计算量大的问题，提出了一种基于改进有限控制集模型预测控制的永磁同步电机直接转矩控制方法，并对该方法进行了实验研究。实验结果表明，与永磁同步电机传统直接转矩控制相比较，该方法可明显减小转矩脉动；同时，与传统有限控制集模型预测控制相比，该方法在计算量上有了大幅度的降低，有利于在更高采样频率的快速动态系统中实现，对控制系统的调试和实现具有重要意义。

［1］HU Hong-ming，ZHU J，GUO You-guang. Model Predictive Control of Permanent Magnet Synchronous Machine with Reduced Torque Ripple[C]//International Conference on Electrical Machines and Systems（ICEMS），2013:1478-1482.

［2］MA Zhi-xun，Kennel S R. Continuous Set Nonlinear Model Predictive Control for PMSM Drives[C]//Power Electronics and Applications，2013:1-10.

［3］郑泽东，王奎，李永东，等．采用模型预测控制的交流电机电流控制器［J］.电工技术学报，2013，28（11）：118-123．

［4］Prenindl M，Bolognani S. Model Predictive Direct Torque Control with Finite Control Set for PMSM Drive Systems，Part 1: Maximum Torque Per Ampere Operation [J]. Industrial Informatics，IEEE Transactions on，2013，9（4）:1912-1921.

［5］Preindl M，Bolognani S.Comparison of Direct and PWM Model Predictive Control for Power Electronic and Drive Systems[C]//Applied Power Electronics Conference and Exposition，2013:2526-2533.

［6］Cortes P，Kazmierkowski M P，Kennel R M，et al.Predictive Control in Power Electronics and Drives[J].Industrial Electronics，IEEE Transactions on，2008，55（12）:4312-4324.

［7］Shuai Wang，Xia Chang-liang，XIN G，et al. A Novel FCSmodel Predictive Control Algorithm with Duty Cycle Optimization for Surface-mounted PMSM[C]//Power Electronics，Machines and Drives（PEMD 2014），7th IET International Conference on，2014:1-6.

［8］Shan Chai，Wang Liu-ping. Finite Control Set Model PreDictive Control of 2LVSI-PMSM Using Interpolated Switching States[C]//IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society，2012:1799-1804.

［9］张永昌，杨海涛.异步电机无速度传感器模型预测控制[J].中国电机工程学报，2014，34（15）：2422-2429.