低速下电机转矩脉动抑制的算法研究

高宽，马钧华

（浙江大学电气工程学院，浙江杭州310027）

在精度较高的伺服控制领域，电机转矩的平稳性是影响系统控制性能的重要因素。实际电机，由于材料、制造工艺等因素或结构的特殊性，单位电流产生的转矩在不同的转子位置角下不尽相同，运行时会有转矩脉动，尤其是在低速时这种转矩脉动引起的速度波动更加明显。

本文提出了一种通过自学习控制的方式，采用迭代算法获取修正曲线，对电机电压进行按位置角的补偿，从而抑制转矩脉动。

1 控制思想概述

针对转矩脉动问题，已有一些国内外学者做过相关研究，并且也取得了一定效果［1-3］。但是许多控制方法都是建立在电机精确的数学模型基础上的，这就限制了在一些难以获得精确数学模型的电机上的应用。本文研究的方法一定程度上克服了这个缺点。

对于理想的电机，单位转矩电流产生的转矩是恒定的。实际的电机因为非理想的对称状态，恒定的转矩电流也会产生转矩脉动，而且脉动是与转子位置角相关且呈周期性的。

本文论述的控制方法并不依赖于电机的数学模型，因此可将电机系统的实际模型看作是一个“黑匣子”，我们只关心其输入与输出。结合实际，我们首先需要对这个“黑匣子”的输入输出特性有个定性的了解。“黑匣子”以电机电压或电流作为输入，以转速或转矩作为输出，则输入输出呈正相关性，这个特性是本文所研究的算法的基础。

基于上述思想，希望通过自学习控制的方式，找出输入输出的具体关系，生成一个修正函数，对输入量（电压或电流）进行修正，使输出量（转速或转矩）恒定，从而实现电机的平稳运行。

2 算法介绍

本文研究的算法主要包括自学习控制和迭代法。

2.1 自学习控制

自学习控制是希望系统能依靠自身的学习功能来认识被控对象的特性，并相应地对系统输入进行调整，从而得到期望的输出特性。

自学习控制的目标是找到一个理想的输入特性曲线，使被控对象输出一个符合期望的结果，即对期望响应Yd(t)，找到控制输入Uk(t)，使系统响应Yk(t)在k →∞时有Yk(t)→Yd(t)，其中k为学习次数。

自学习控制系统的结构如图1所示。其控制过程如下：系统输入U(t)，检测系统响应Y(t)，经过自学习控制模块后得到修正曲线，将其存入存储器，然后对系统输入进行修正，得到修正后的输入Uk(t)，系统响应为Yk(t)，再将Yk(t)输入自学习模块，如此不断学习，最终得到期望的系统响应Yd(t)。此自学习控制与下面2.2 节介绍的迭代法共同构成迭代学习控制算法［4］。

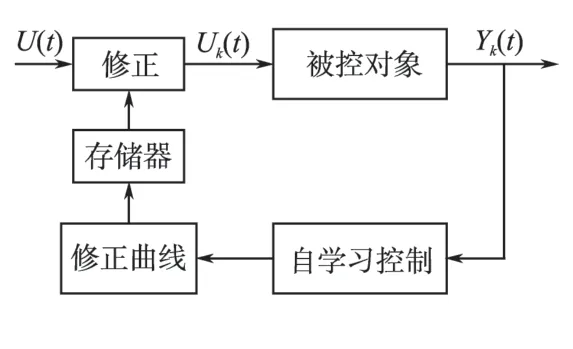
图1 自学习控制系统Fig.1 Self-learning control system

2.2 迭代法

迭代法是一种逐次逼近法，其基本原理是不断用变量的旧值递推得到新值。迭代法要取得成功，关键是找到一个合适的变量递推函数，即迭代函数，使得变量能收敛于稳定值［7］。

一般地，对于递增函数y=f（x），欲使y=a，若对自变量x作如下迭代：

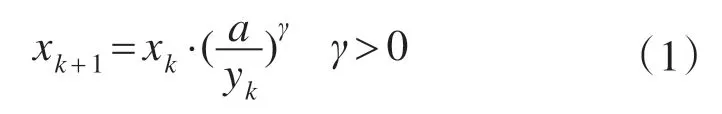
其中yk=f（xk），取合适的γ值，可使迭代收敛快而平稳。选定γ值后，若xk和yk收敛，则对式（1）两边取极得

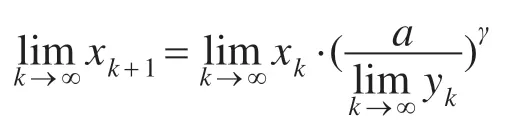
对于电机系统，电机转速n 与电压大小U 成正比，即n 与U 存在递增的函数关系n=f（U）。因此可作猜想：运用上述迭代方法，转速n可收敛于稳定值。

2.3 算法应用

将上述算法具体应用到电机转矩脉动的抑制中去，算法流程图如图2所示。

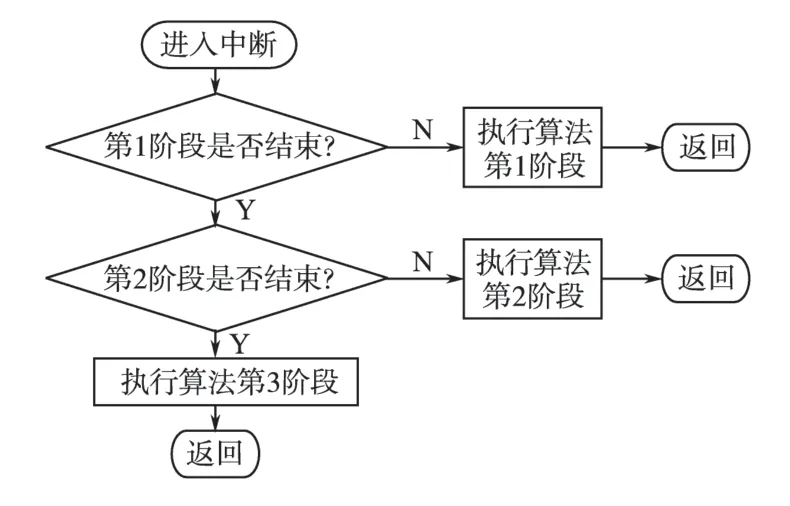
图2 算法流程图Fig.2 Flow chart of the algorithm

本算法主要通过自学习方式获得电机的脉动转速与电机转子位置角θ（电角度）之间的关系式n=g(θ)，然后利用此关系式，采用迭代法对电机电压进行按位置角的前馈补偿，使电机转速趋于平稳。算法具体执行有3个阶段，分别如下。

第1 阶段：利用转速PID 调节器给定转速运行。本文实验电机系统采用调压调速，采集电压斩波PWM 的占空比，多次采样取平均值得到平均占空比，这可以反映给定转速下的平均电压第1 阶段结束后不再使用转速PID 调节器。

第2 阶段：使用第1 阶段计算得到的平均占空比（-D），使电机在平均电压（-U）下运行。采集电机实际转速n与对应的转子位置角θ，得到两者之间的关系式n=g1（θ）。

第3 阶段：利用第2 阶段获得的关系式n=g1（θ）对平均占空比（-D）按位置角进行第1次修正，使电机按与位置角关联的占空比D=h1（θ）运行。根据修正后的运行结果可得到新的关系式n=g2（θ），然后对占空比进行第2次修正，得到D=h2（θ）。以此类推，重复迭代。每次迭代后刷新得到n=gk（θ）和D=hk（θ），用数组来存放。迭代次数可由程序设置，也可以按转速n的脉动情况来自动控制。

3 实验结果及分析

实验在一台永磁同步电机上进行，电机额定线电压220 V，额定转速3 000 r/min，极对数为4，光电编码器线数为2 500。由于实验研究的是电机的低速特性，为了增大电压PWM 占空比的分辨率，提高实验精度，实验时特意降低电压，设定电机驱动部分的逆变电路直流侧母线电压UZK=24 V。设定功率开关IGBT的开关频率为7.5 kHz。

为了模拟本身具有大转矩脉动的电机特性，本实验电机按照无刷直流电机三相六状态的方式运行，且特别修改了无刷电机的触发角（正常情况下，换相完成瞬间定子磁势方向超前永磁体转子磁势120°（电角度）；本实验修改这个角度为60°（电角度），使得电机本身的单位电流转矩呈现明显的位置相关性（定子磁势与永磁体转子磁势叉积的大小反映了电磁转矩的大小）［8］。为了消除外界随机的转矩脉动影响，实验中安置了一个与被试电机相同的同轴相接的电机做发电机，用于产生负载转矩，即使这个负载转矩有脉动，也是与位置角成确定关系的，可以合并到被试电机的转矩脉动中去，故不影响本实验方法的有效性。

实验数据均采用标幺值形式，转速基值为电机额定转速，电角度基值为2π。

给定转速n=0.01（标幺值），用最优参数的PID调节器控制的电机转速波形和转子位置波形分别如图3、图4所示。从图3中可以明显看到转速在1 个电角度周期内产生了6 次脉动，这对应着电机的6次换相。

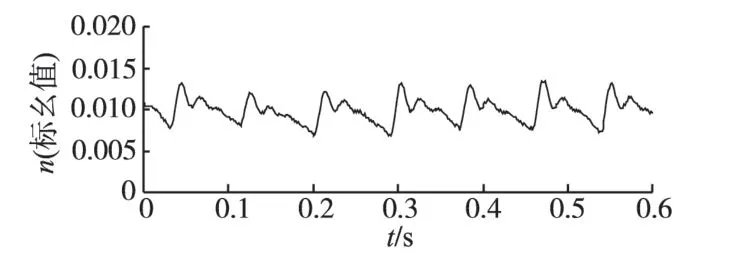
图3 转速波形Fig.3 Speed waveform

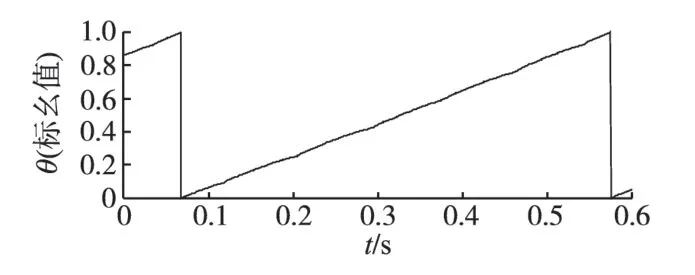
图4 转子位置波形Fig.4 Rotor position waveform

转速围绕给定转速n=0.01（标幺值）脉动，转速最大值为0.013 431（标幺值），最小值为0.006 822（标幺值）。定义转速脉动比为

则最大脉动比为34.31%。实验中利用传统的PID 调节器，选取最优参数依然难以使电机转速变得平稳。接下来具体应用本文算法进行实验。

第1阶段：给定转速n=0.01（标幺值），测得平均占空比平均电压

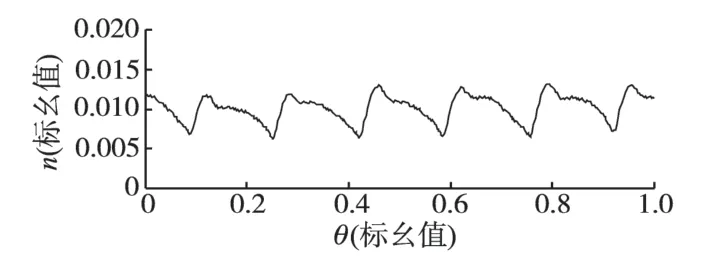
图5 脉动转速与转子位置角关系曲线Fig.5 Relation between ripple speed and rotor position electrical angle

第3阶段：利用关系式n=g1（θ）求得转速平均值nˉ=0.010 3（标幺值），与给定转速n=0.01（标幺值）基本一致，可见转速是围绕给定转速脉动的，可将转速平均值nˉ作为平稳转速的期望值。由于转速与电压大小关系符合迭代法的条件，参照式（1），且实验证明，取γ=1 较优，于是对任意位置角θ下可作如下迭代：

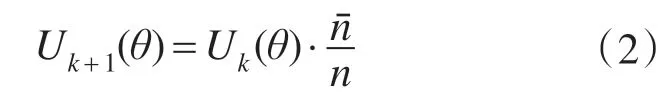
其实质是根据转速n 偏离平均值nˉ的比例关系对电压大小进行修正。相应的PWM占空比形式为和Dk(θ)的值根据当前转子位置角θ分别从存放关系式n=gk（θ）和D=hk（θ）的数组中取得。每次迭代后需刷新关系式n=gk（θ）和D=hk（θ）。下面看一下算法对抑制转速脉动的效果。

图6给出了经过5次，20次，50次迭代后的转速波形以及经过50次迭代后的转子位置波形。

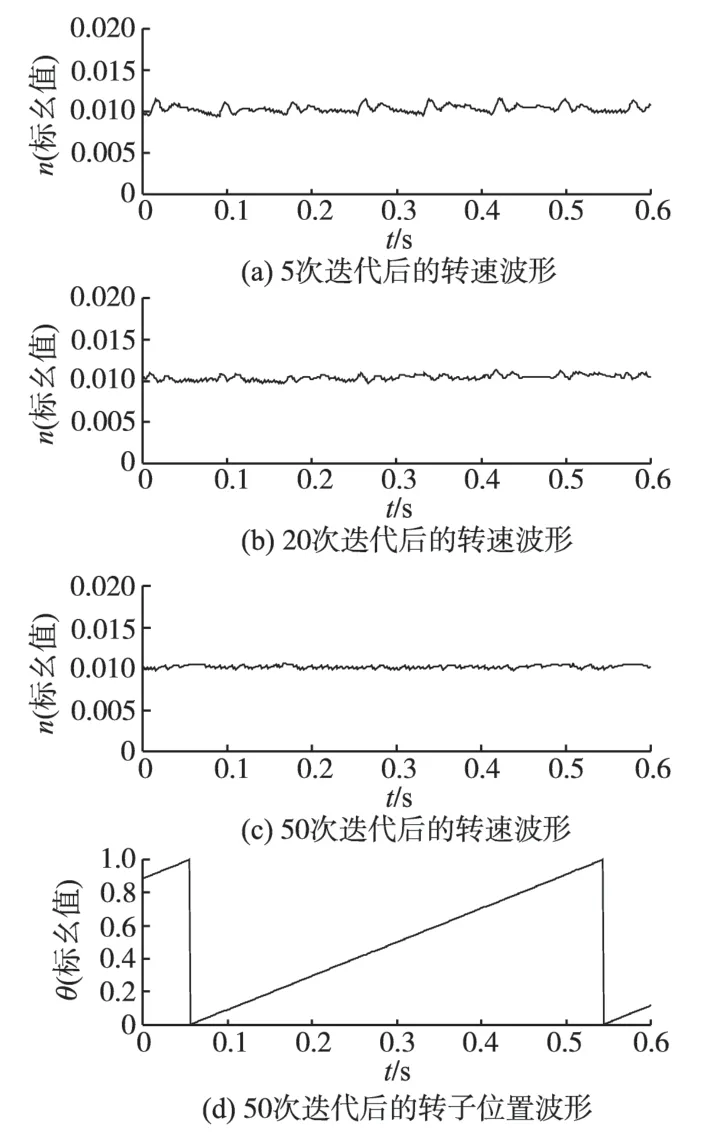
图6 迭代后转速及转子位置波形图Fig.6 Speed and rotor position waveforms after iteration

转速脉动抑制效果与迭代次数的关系见表1。

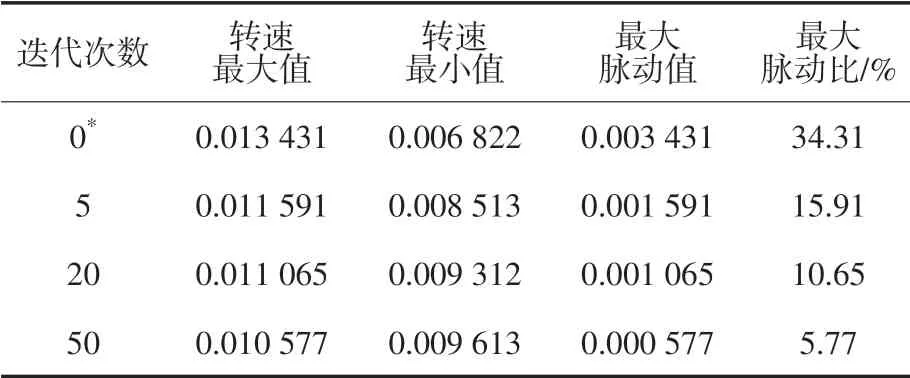
表1 转速脉动抑制效果Tab.1 Result of reducing speed ripple

表1中，“*”为迭代次数0表示未经算法控制的原始转速数据。

图7给出了电机转速的最大脉动比与迭代次数的关系曲线。

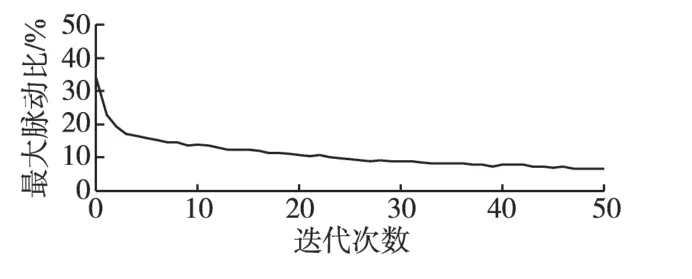
图7 最大脉动比与迭代次数的关系Fig.7 Relation between maximum ripple ratio and iterations

从以上实验结果中可以直观地看到随着迭代次数的增加，电机转速脉动逐渐减小。经过50 次迭代后，最大脉动值从最初的0.003 431（标幺值）降低到0.000 577（标幺值），最大脉动比从最初的34.31%降低到5.77%，转速脉动得到了很好的抑制，转速波形基本平稳。观察比较图4 和图6 的转子位置波形，后者线性度更好，更加平滑，说明电机运行更加平稳。实验表明，经过10～20 次迭代后转速平稳度即可令人满意，在转速n=0.01（标幺值）下，1 个电角度周期约为0.5 s（极对数为4），完成10～20 次迭代约需5～10 s。

经过多次迭代，待转速平稳后测得占空比与转子位置角的关系如图8所示。

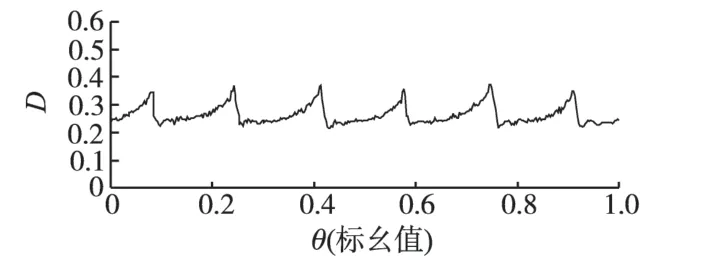
图8 占空比与转子位置角关系曲线Fig.8 Relation between duty ratio and rotor position electrical angle

按此关系对电压进行修正即可获得较平稳的转速。可以将此关系存入存储器，以后即可直接调用来对电压进行修正。根据前文论述，利用传统的PID 调节器难以使得转速变得平稳，下面我们对PID 调节器的输出进行修正，改进后的控制结构图如图9所示。

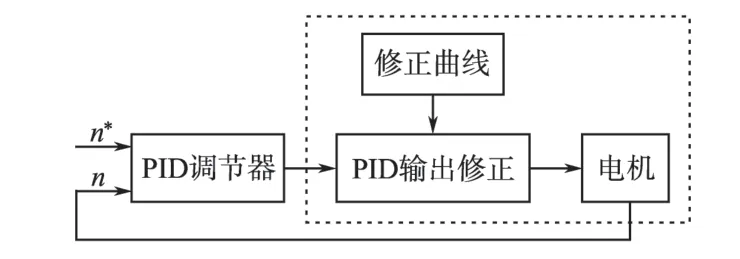
图9 PID调节器输出修正的结构图Fig.9 Structure diagram of the improved PID regulator

对转速PID 调节器的输出按照图8 所示曲线的规律进行修正。可以将图9 虚线框内的结构看作一个“新电机”，这个“新电机”具有良好的控制特性，即单位电流转矩不随位置角变化。在PID 参数最优时“新电机”的转速曲线如图10所示。

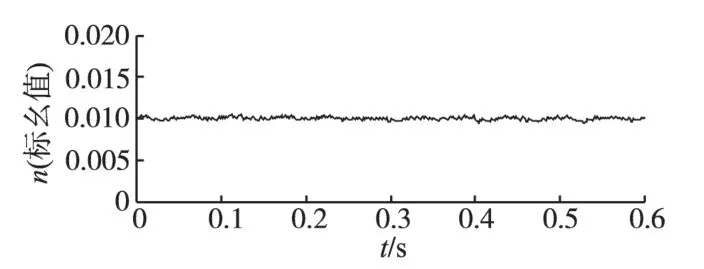
图10 “新电机”的转速曲线Fig.10 Speed waveform of the“new motor”

“新电机”的最大脉动比为5.93%，相比改进前的最大脉动比34.31%，“新电机”的转速特性取得了明显的改善。

为考察这一修正曲线的通用性，观察转速n=0.005（标幺值）时的实验结果，如图11所示。

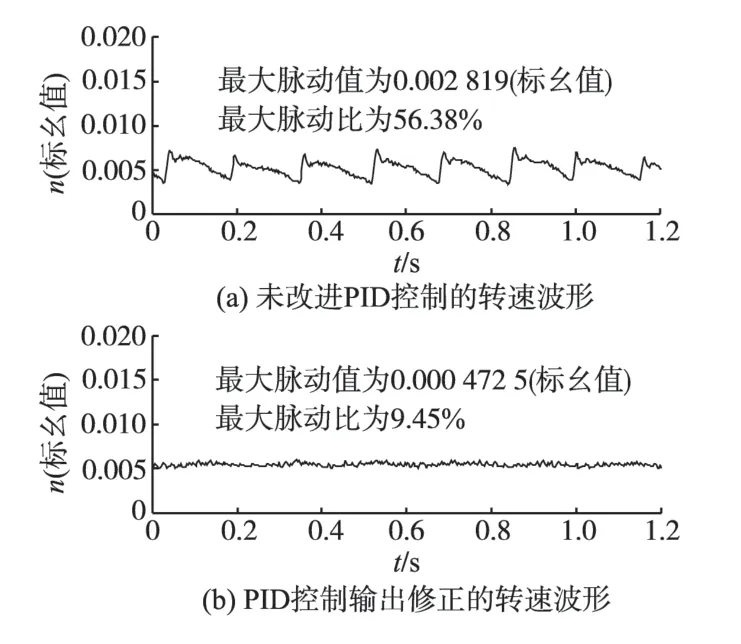
图11 n=0.005（标幺值）时的转速波形比较Fig.11 Comparison of speed waveforms when n=0.005（pu）

由图11可知，运用了PID调节器输出修正之后，n=0.005（标幺值）运行时的最大转速脉动比也由56.38%下降到9.45%，转速脉动同样得到了很好的抑制。实验证明，本文算法对低速下电机转速脉动的抑制具有通用性，对不同电机不同转速下的转速脉动抑制均具有良好的效果。

4 结论

本文提出的迭代学习控制算法，不需要获得电机系统精确的数学模型，仅需凭借系统输入输出的正相关性，即可对系统输出特性进行有效控制。实验证明该算法对低速下电机转矩脉动的抑制具有较好的效果，主要体现在两方面：1）较快的收敛速度。只需经过10～20次迭代即可取得令人满意的结果；2）较高的平稳度。从实验数据中可以看出，经过算法控制后，转速脉动得到了大幅度的抑制，电机运行非常平稳。

最后，对本文算法可作进一步猜想：该算法不仅对低速下电机转矩脉动的抑制有效，对其他输入输出呈正相关性的系统的控制同样有效。

［1］Qian Weizhe，Panda S K，Xu J X. Speed Ripple Minimization in PM Synchronous Motor Using Iterative Learning Control［J］.IEEE Transactions on Energy Conversion，2005，20（1）：53-61.

［2］张猛，李永东，赵铁夫，等.一种减小变频空调压缩机低速范围内转速脉动的方法［J］.电工技术学报，2006，21（7）：99-104.

［3］储剑波，胡育文，黄文新，等.一种抑制永磁同步电机转速脉动的方法［J］.电工技术学报，2009，24（12）：43-48.

［4］李叶松，董玮，秦忆.运动控制系统自学习问题研究［J］.华中科技大学学报，2001，29（1）：66-69.

［5］石成英，林辉.迭代学习控制的研究与应用进展［J］.测控技术，2004，23（2）：1-7.

［6］胡玉娥，翟春艳.迭代学习控制现状与展望［J］.自动化仪表，2005，26（6）：1-4.

［7］易大义，沈云宝，李有法.计算方法［M］.杭州：浙江大学出版社，2002.

［8］贺益康，许大中.电机控制［M］.杭州：浙江大学出版社，2010.