永磁同步电机自抗扰控制技术研究

李婉婷，厉虹

（北京信息科技大学自动化学院，北京100192）

交流电机中，永磁同步电机（PMSM）具有多变量非线性强耦合的特点，由其构成的电气传动系统采用常规PI控制器［1-2］难以应付大负载和多变扰动的工况，基于高性能控制策略PMSM调速系统已经成为主流。随着控制理论的发展，基于非线性控制理论［3］的新型控制策略如：反推控制［4］、反馈线性化［5］、逆系统［6］、无源控制［7］以及自抗扰控制（ADRC）［8］等相继问世，如按照无源控制理论设计的无源控制器可提高系统的全局稳定性，对系统参数变化及外来扰动有较强的鲁棒性；而依据自抗扰控制理论设计的ADRC控制器，也具有不依赖数学模型，适用性较强的优点。

无位置传感器［9］控制系统无需检测硬件，免去了位置传感器带来的种种麻烦，可提高系统可靠性，降低系统成本。无位置传感器系统最重要的是如何准确地获取转速信息且保持较高控制精度、满足实时控制的要求。准确估计转子速度和位置的方法按速度高低分类主要有：适用于中高速调速系统的开环估计法［10］、观测器估计法［11］和智能控制理论估算法［12］，适用于低速系统的高频注入法［13］以及适用于转子初始位置检测的INFORM电感法［14］等。

本文将非线性自抗扰控制理论与无位置传感技术相结合应用于PMSM矢量控制系统，设计了ADRC速度调节器，与PI速度调节器相比，ADRC不依赖数学模型，响应速度快，抗干扰性强；采用模型参考自适应（MRAS）策略估计转子速度和位置［15］，由于MRAS只需要检测定子电流和直流母线电压，因此具有模型简单可靠等优点。最后通过仿真实验验证了所提出方法的有效性。

1 基于MRAS的PMSM矢量控制

1.1 PMSM数学模型

PMSM在d-q轴同步旋转坐标系下的定子电流方程［16］为

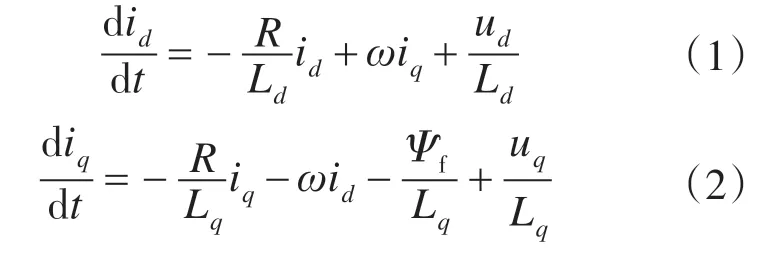
电磁转矩方程为

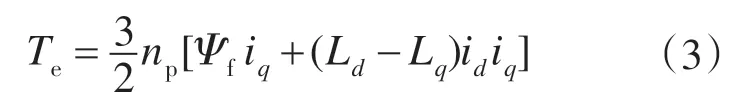
式中：ud，uq为定子绕组d-q轴电压；id，iq为定子绕组d-q轴电流；Ld，Lq为定子绕组d-q轴电感，由于所用永磁同步电机为隐极式电机，则Ld=Lq=L，以下公式中定子绕组d-q轴电感均以L表示；R为定子电阻；Ψf为转子永久磁铁产生的磁势；ω为转子速度；np为电机极对数。

1.2 MRAS转子速度估计

MRAS的主要思想是将含有待估参数的方程与不含未知参数的方程分别作为可调模型与参考模型，针对具有相同物理意义的输出量差值构造合适的自适应率，使控制对象的输出跟踪参考模型的输出［17］。根据稳定性原理得到电机转速估计自适应公式，根据波波夫超稳定理论保证转速的渐进收敛性。

由于转子速度ω已经包含在PMSM数学模型里，此处选择永磁同步电机的电流模型作为可调模型，PMSM模型为参考模型。

将式（1）、式（2）写成矩阵形式：

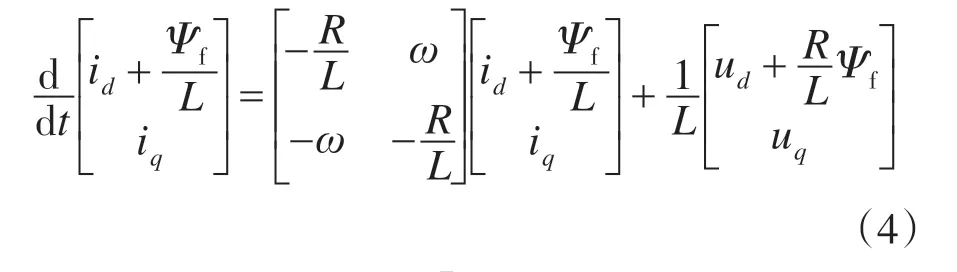
令

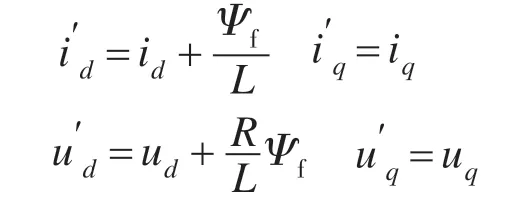
式（4）可改写为

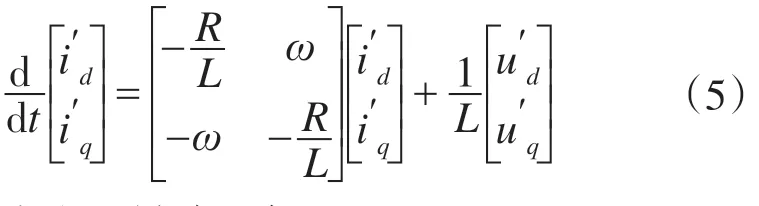
为分析问题方便，令

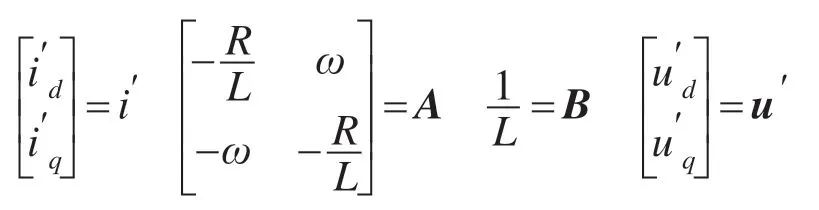
得到简化形式为

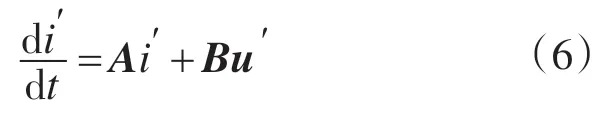
则式（5）以估计值可表示为

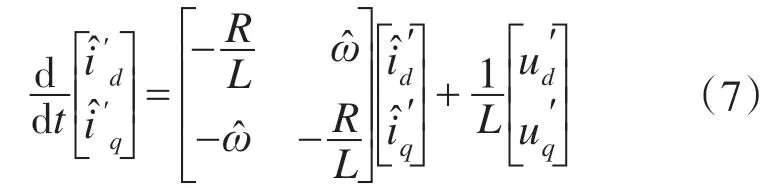
或

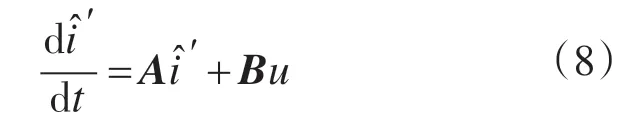
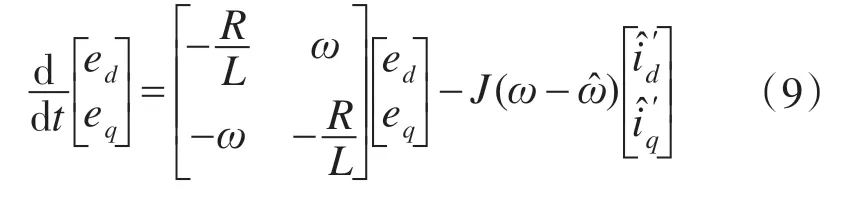
为了分析方便，将式（9）简化成以下形式：

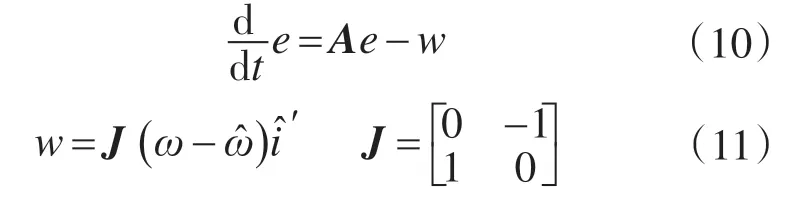
根据波波夫稳定性理论，欲使系统保持稳定，须满足2个条件［18］：

1）H(s)=D(sI-A)-1是严格的正实性矩阵；

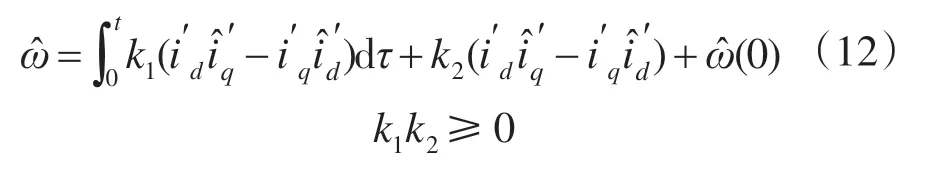
用id，iq代替得到：

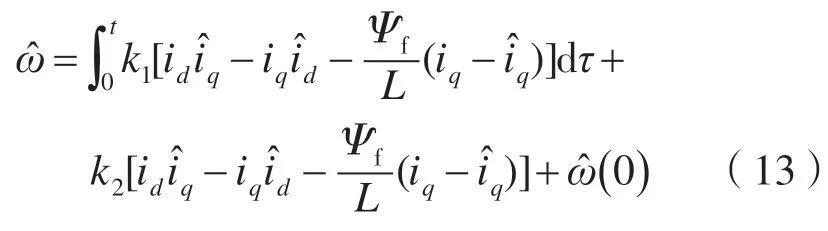
式（13）中的id，iq可以通过测量的定子电流计算得出，而则可根据可调模型式（7）的计算得到，上述式中的k1和k2是需要调整的参数。转子位置计算公式如下：

根据上述公式得到MRAS 结构原理框图如图1所示。

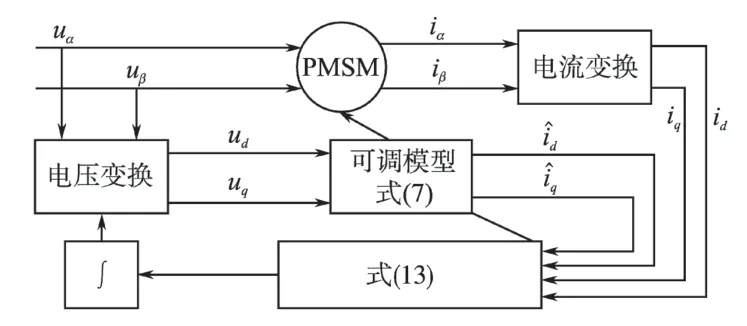
图1 MRAS结构原理框图Fig.1 The block diagram of MRAS

2 ADRC设计

根据自抗扰控制理论设计的自抗扰控制器ADRC 一般由3 部分组成：非线性跟踪微分器（tracking differentiator，TD）、扩张状态观测器（extended state observer，ESO）和非线性状态误差反馈（nonlinear state error feedback，NLSEF）［19］。则标准n阶ADRC控制器结构框图如图2所示。

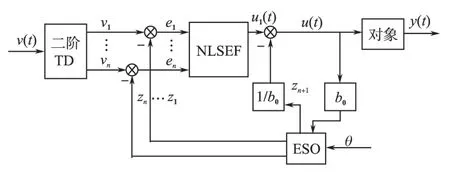
图2 自抗扰控制器结构框图Fig.2 The block diagram of ADRC

依据自抗扰技术原理构造二阶自抗扰控制器，得到转速外环q 轴控制器，其中一阶离散跟踪-微分器：

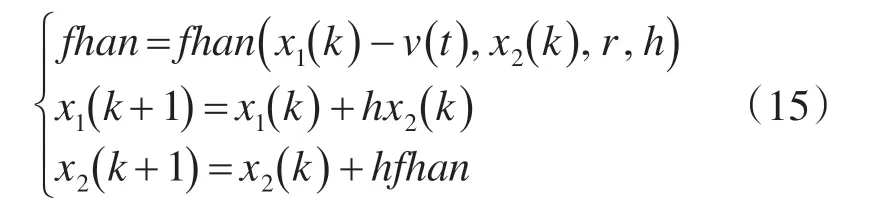
式中：v(t)为ADRC控制器的输入信号；x1(k)为输入信号的跟踪信号；x2(k)为x1(k)的微分形式；r为跟踪速度因子；h为微积分步长；fhan函数为非线性函数。fhan函数能解决其它函数在直接离散化后系统进入稳态时产生的高频震颤问题，一阶离散跟踪-微分器跟踪信号的能力取决于r，r越大，x1(k)跟踪v(t)能力越强，当r大到一定程度，影响跟踪微分器的性能。

二阶扩张状态观测器：

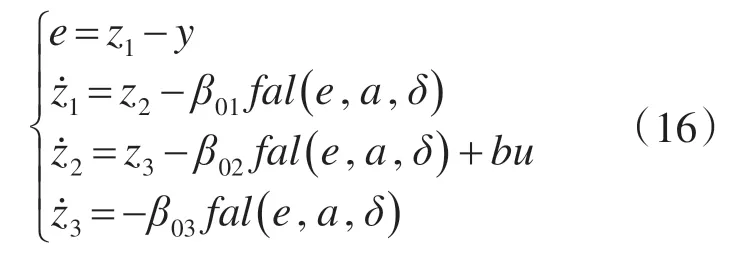
式中：y 为系统的反馈信号也就是ESO 的输入信号，即系统的速度反馈信号；z1为速度反馈信号的跟踪信号；e为输入与反馈的误差信号；z2为x2(k)的跟踪信号；z3为总扰动的观测值；β01，β02，β03为输出误差校正增益；fal()ε’a’δ 为最优综合控制函数；δ为滤波因子；β01，β02，β03为可选取参数也是ESO重点调整参数。

对于n阶对象，传统的状态观测器是n维的，但是ESO 输出是n+1 维的。正是这拓展出来的第n+1维状态，使ESO具备了独特的功能。

fal函数的表达式为

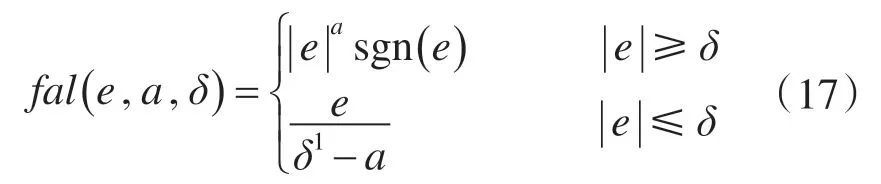
式中：a为0～1的常数，a越小，跟踪越快，但滤波效果会变差；δ为影响滤波效果的常数，δ变大，滤波效果变好。

非线性反馈控制率：

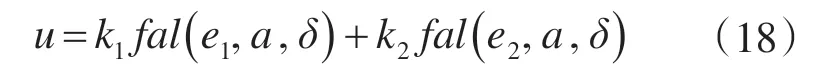
在NLSEF 中，需要对参数k1和k2进行反复调整，才能得到合适的控制率。

根据式（2），隐极式PMSMLd=Lq，则转速输出方程可写成：

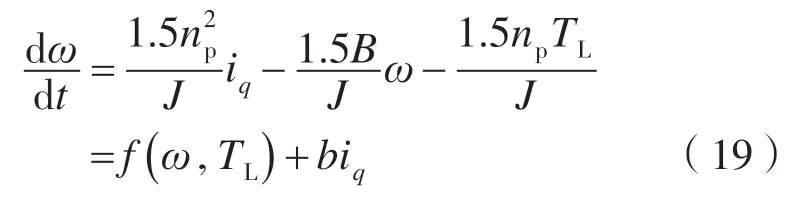
其中

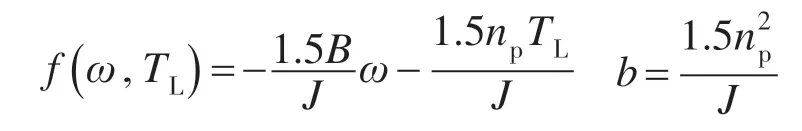
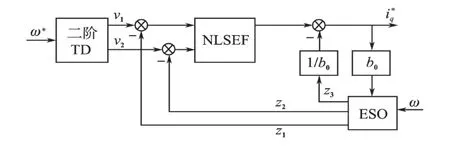
图3 PMSM速度调节器结构框图Fig.3 The block diagram of speed regulator for PMSM

3 仿真实验

依照图1 所示的MRAS 结构原理和式（7）、式（13）、式（14），可以估算出转子速度ω和θ^，代替光电编码器的速度检测作用，将估算出来的转子速度送入ADRC控制器的输入端，同时将基于PI调节的速度控制器替换成ADRC控制器，依据图3 和式（15）～式（18）完成ADRC 速度调节器的建模，由于ADRC不依赖于数学模型，通用性较强，只需调节β01，β02，β03，k1和k2即可，这样即完成了速度估算与ADRC 控制器相结合的整个矢量控制系统。原理图如图4所示。图4中的PI为电流调节器，而速度调节采用了ADRC策略。

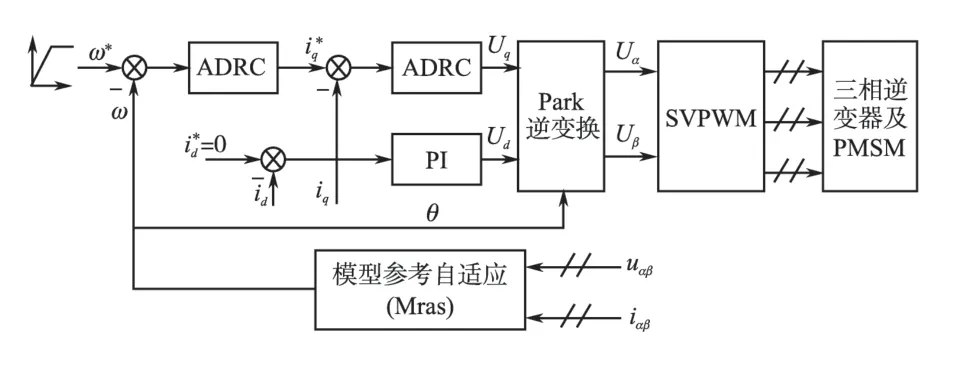
图4 ADRC与MRAS结合的PMSM矢量控制系统框图Fig.4 The block diagram of ADRC combining with MRAS for PMSM vector control system

为了验证所设计的控制策略的有效性，在Matlab/Simulink 环境下进行仿真实验。实验所用PMSM 参数为：极对数np=4，给定转速ω*=1 400 r/min，定子电阻R=2.875 Ω，d-q轴电感Ld=Lq=L=8.5 mH ，转子磁动势Ψf=0.175 Wb，转动惯量J=0.8×10-3kg·m2，摩擦系数B=0。

依据图3和式（15）～式（18），对ADRC调节器建模，并对图3中的TD，ESO和NLESF的参数进行调整。TD 中有r和h 2 个参数，仿真实验显示，当r=2 000，h=0.01时，跟踪效果最好，滤波效果显著。ESO中参数较多，也是调整的重点，a为0～1 的常数，选取a=0.5，δ=0.1时跟踪快，滤波效果好。β01，β02和β03的选取影响ESO的收敛速度，因此选取β01=25 000，β02=10，β03=-1。NLSEF 中的k1和k2是决定补偿强弱的“补偿因子”，作为可调参数用，选取k1=12，k2=12。依照图1 的MRAS 结构原理，搭建MRAS 仿真模型，选择参数为k1=16.5，k2=1。

图5是ADRC控制器下实际转速响应曲线和估计转速响应曲线，给定转速为1 400 r/min，启动负载为3 N·m，在0.1 s时突加负载到6 N·m。

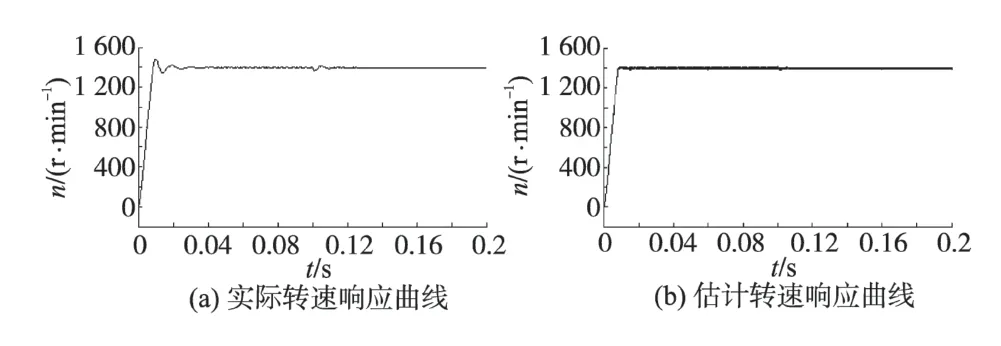
图5 ADRC转速响应曲线Fig.5 Dynamic respond of speed for ADRC

观察图5 的实验曲线表明，ADRC 与MRAS结合的无位置传感器矢量控制系统具有较好的动态和稳态性能，在时间0.02 s 时转速进入稳定状态，超调时间短。MRAS 有较好的转速估计能力，在0.1 s 突加负载时，实际转速与估计转速基本不受负载影响，表现出较强的抗干扰能力。

当转速调节器为PI 时，反复调整其参数为：转速环，KP=1，KI=0.05；电流环，KP=17，KI=6 000。两组实验所得到的转速响应曲线对比如图6 所示。图6 中，给定转速为1 400 r/min，启动负载为3 N·m，在0.1 s 时突加负载到6 N·m。

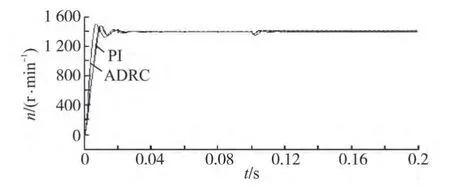
图6 转速响应曲线Fig.6 Dynamic respond of speed

观察图6 的响应曲线，采用ADRC 策略时，转速响应时间较短，可以较快地进入稳定状态；在0.1 s 突加负载到6 N·m 时，ADRC 控制时的转速能很快恢复到给定值，而PI 控制时，系统受到干扰后，转速波动明显，且不能恢复到系统的给定值，表明ADRC控制器的快速性和抗干扰能力较强。

图7和图8为采用两种控制策略时的转矩响应和电流响应曲线。当给定转速为1 400 r/min，加负载为3 N·m时启动，在0.1 s时突加负载到6 N·m。

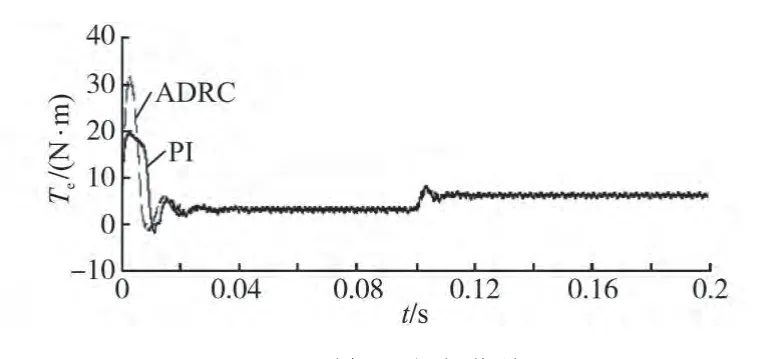
图7 转矩响应曲线Fig.7 Dynamic respond of torque

图7曲线表明，ADRC控制时，转矩响应曲线比较平滑稳定，系统稳定性较好；而PI 控制时转矩响应曲线波动较大，稳态误差大，表明ADRC控制器具有较好的滤波效果。

图8的电流响应曲线表明，ADRC控制时，三相电流曲线是比较光滑的正弦曲线，而PI 控制时，三相电流曲线含有较多的畸变量，表明ADRC控制器具有较好的滤波效果。

控制器为ADRC 和PI 时的d-q轴电流响应曲线如图9所示。

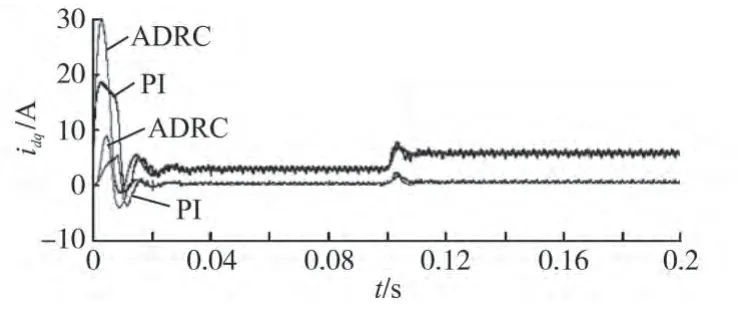
图9 d-q轴电流响应曲线Fig.9 Dynamic respond of current for d-q rotating

图9中，控制器为ADRC 的d-q轴电流曲线平滑稳定，而PI控制时的d-q轴电流稳态响应波动较大，稳态误差大，表明采用ADRC 控制策略时，系统更加稳定。

4 结论

本文将非线性自抗扰控制理论与无位置传感技术相结合，在永磁同步电动机矢量控制系统中设计了自抗扰速度调节器，采用模型参考自适应策略估算转子速度和转子位置，提高系统稳定性和抗扰性。以隐极式永磁同步电机为实例的仿真实验表明：MARS算法能够精确地估算转子速度和转子位置，速度调节中，ADRC 控制器较传统的PI 控制器，具有响应速度快，抗干扰能力强及鲁棒性强等优点，它的应用丰富了永磁同步电机控制策略，具有一定的工程应用意义。

［1］崔业兵，向方明，朱遵义，等.智能优化PI 参数的永磁同步电机控制［J］.电机与控制应用，2013，40（8）：23-28.

［2］王莉娜，朱鸿悦，杨宗军.永磁同步电动机调速系统PI控制器参数整定方法［J］.电工技术学报，2014，29（5）：104-117.

［3］王久和.电机现代控制技术［M］.北京：科学出版社，2006.

［4］刘栋良，郑谢辉，崔丽丽.无速度传感器永磁同步电机反推控制［J］.电工技术学报，2011，26（9）：67-72.

［5］刘小河，王鹤华.基于SVPWM永磁同步电机反馈线性化控制［J］.现代电子技术，2013，36（12）：159-162.

［6］费德成，朱熀秋.基于逆系统理论的无轴承永磁同步电机解耦控制研究［J］.中国工程科学，2005，7（11）：52-58.

［7］王芳媛.基于无源性的永磁同步电机高性能速度控制研究［D］.广州：华南理工大学，2012.

［8］顾问，王久和，徐升升，等.基于自抗扰控制的永磁同步电机矢量控制策略［J］.电源学报，2011，9（5）：65-68.

［9］黄涛. 永磁同步电机无速度传感器矢量控制系统的研究［D］.天津：天津大学，2007.

［10］Naidu M，Bose B K. Rotor Position Estimation Scheme of a Permanent Magnet Synchronous Machine for High Performance Variable Speed Drive［C］//Industry Applications Society Annual Meeting，1992：48-53.

［11］王润博. 永磁同步电机无位置传感器矢量控制系统研究［D］.北京：北方工业大学，2013.

［12］肖杨柳.基于模糊控制的永磁同步电机无位置传感器驱动系统［D］.长沙：湖南大学，2010.

［13］Piippo A，Hinkkanen M，Luomi J.Sensorless Control of PMSM Drives Using Acombination of Voltage Model and HF Signal Injection［C］//Industr Applications Conferenc，2004：964-970.

［14］刘颖，周波，李帅，等.转子磁钢表贴式永磁同步电机转子初始位置检测［J］中国电机工程学报，2011，31（18）：48-54.

［15］Liang Yan，Li Yongdong. Sensorless Control of PM Synchronous Motors Based on MRAS Method and Initial Position Estimation［C］//Electrical Machines and Systems，2003：96-99.

［16］王春民，嵇艳鞠，栾卉，等.MATLAB/SIMULINK永磁同步电机矢量控制系统仿真［J］. 吉林大学学报：信息科学版，2009，27（1）：17-22.

［17］常凯.基于模型参考自适应的永磁同步电机无速度传感器控制系统的设计［D］.沈阳：东北大学，2009.

［18］Benjak O，Gerling D. Review of Position Estimation Methods for IPMSM Drives Without a Position Sensor Part I：Nonadaptive Methods［C］//Electrical Machines ICEM，2010：6-8.

［19］孙凯，许镇琳，盖廓，等.基于自抗扰控制器的永磁同步电机位置伺服系统［J］.中国电机工程学报，2007，27（15）：43-46.