思想无形 渗透有痕
林德英
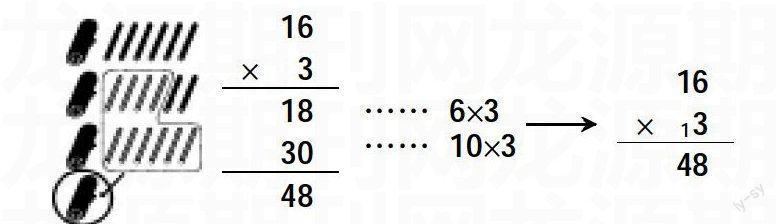

摘 要:数学思想常常隐含在数学知识体系中,是无“形”的。教师只有把握住数学思想,才能高屋建瓴,对教材进行再创造。教师要提高对渗透数学思想重要性的认识,要结合不同阶段、不同内容的知识教学,有意识地进行孕育和渗透。
关键词:数学思想;孕育;渗透
日本著名数学教育家米山国藏指出:“成功的数学教育,应当是数学的精神、思想方法深深铭刻在学生的头脑中,长久地活跃于他们日常的业务中,虽然那时,数学知识可能淡忘了。”数学知识,如,概念、法则、性质、公式等都可以明显地写在教材中,是有“形”的,而数学思想,如,分类、转化、极限、数形结合等却隐含在数学知识体系中,是无“形”的。数学思想是数学的灵魂,我们在数学课堂教学过程中,要结合教学内容,对教材进行认真分析、深入解读,进行再创造,挖掘出教材中隐含的数学思想,才可以使学生对数学知识理解的同时,提升学生的数学素养,提高学生的学习能力。
一、在性质教学中渗透建模思想
新课标明确指出:“让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程,进而使学生获得对数学理解的同时,在思维能力、情感态度与价值观等多方面获得进步和发展。”在数学中,我们可以把概念、法则、定理等知识看作是数学模型,在建立和运用这些概念、法则、定理的过程中,我们就可以向学生渗透数学模型思想。模型思想既然作为一种基本的数学思想,如何在数学课堂中开展有效的建模活动呢?
我们在进行数学建模时,可以先从学生熟悉的生活情境中选择鲜活贴切的数学素材,引导学生通过数学活动,利用已有的生活经验,将数学模型激活并提取出来。如,“商不变的性质”的教学,先用猴王分桃的故事导入,师:花果山风景秀丽,气候宜人,那里住着一群猴子。有一天,猴王给小猴分桃子。猴王说:“给你6个桃子,平均分给你们3只小猴吧。”小猴子听了,我只能得到2个桃子,连连摇头说:“太少了,太少了。”猴王又说:“好吧,给你60个桃子,平均分给你们30只小猴,怎么样?”小猴子得寸进尺,挠挠头皮,试探地说:“大王,再多给点行不行啊?”猴王一拍大腿,显示出慷慨大度的样子:“那好吧,给你600个桃子,平均分给你们300只小猴,你总该满意了吧?”小猴子觉得占了大便宜,开心地笑了,猴王也笑了。设疑:谁是聪明的一笑?为什么?你是怎么知道的?得出算式:6÷3=2
60÷30=2 600÷300=2发现和提出问题是数学建模的起点,情境中蕴藏着引发思考的数学信息,让学生从情境中提炼出数学问题,作为数学探索的切入点,有利于学生在自然的状态下,从生活向数学过渡,为有效的建模打下坚实的基础。接着,再让学生自己写一组数据,观察算式,看看发现了什么?通过学生板演,再继续追问,被除数怎么变了?除数怎么变了?通过全班学生共同的讨论,不断的补充、修改,自己得出商不变的性质,让学生用语言或算式把结论写出来,从而形成有效的数学模型。
著名教育家皮亚杰认为:“对知识的理解是学习者自己主动的构建知识的意义的过程。”建模的教学,不像数学知识点一样可以独立出来进行专门教学,而是学生在学习过程中逐渐领悟,通过问题情境—建立模型—解决问题—拓展运用,让学生在理解知识的同时,在思维能力方面获得进一步的发展。
二、在计算教学中渗透数形结合思想
数学家华罗庚先生说过:“数缺形时少直观,形少数时难入微,数形结合百般好,隔裂分家万事休。”通过数形结合,我们可以把抽象问题形象化,复杂问题简单化。教师在教学过程中解决问题时,要有渗透数形结合思想的意识。
如,三年级上册《进位笔算乘法》16×3的教学。教师可以通过创设买连环画的情境,出示一套连环画16本,(3套)王老师一共买了多少本连环画?给学生提供小棒图,在练习卡上圈一圈,并不断引导学生想一想,让学生理解每一步乘法的计算意义,明确算理,掌握算法。
问题:1.谁能借助小棒图说一说你是怎样算的?这一捆是怎么得到的?
2.这种竖式计算的方法你们明白吗?18表示什么意思?30表示什么意思?48是怎么得到的呢?
3.比较摆小棒和竖式计算的方法,你发现了什么?
4.为了书写简便,竖式可以这样写,这个1表示什么意思?为什么写在这?十位上的4是怎样得到的?
5.谁能完整地说一说竖式计算时要注意什么?先算什么?再算什么?
算理是数学学习的重要内容,利用“形”的生动性、直观性,探索、感悟算理的形成过程,有助于学生对知识本质的把握。学生在操作中利用形的直观性,从而抽象成数的抽象性,不仅可以较为深刻地理解算理,形象思维和逻辑思维也得到了发展。以上数形结合的办法,既强化了算法,又让学生深刻理解了算理,数形结合相得益彰,不仅知其然还知其所以然。
三、在面积教学中渗透转化思想
转化也称化归,它是指将未知的,陌生的,复杂的问题通过演绎归纳转化为已知的,熟悉的,简单的问题,从而使问题顺利解决的数学思想。转化思想蕴含在数学知识的形成过程中,是数学知识高层次上的抽象和概括,也是小学学习数学的一种重要的思想。我们在教学中应该注重适时渗透转化思想,让学生掌握转化的方法,为学生的后续学习积攒后劲。
如,“梯形面积的计算”教学,转化思想是“梯形面积”的灵魂。这节课怎样以“转化”作为教学的主线,通过有效的数学教学活动,探究知识的“来龙去脉”,让学生通过建构数学知识技能,积累活动经验,感悟数学思想?我是这样设计的:在学习梯形面积之前,关注学生已有的转化的活动经验。首先请学生认真观察,你看懂了什么?(如图)
以此引领学生回顾小数乘法和三角形的面积推导公式,激活学生已有的活动经验,把新的问题转化为已学的知识来解决,引出梯形面积。
接着我给学生提供了多种的梯形学具,让学生通过剪一剪、拼一拼,留给学生足够的时空自主探索,把梯形转化为我们已经学过的图形,从而保证转化的有效性。在学生作品的展示过程中,追问:转化后的图形和原来的梯形相比,它们的面积大小有什么关系?学完梯形面积之后,为关注学生深入体会转化思想,我还通过三个问题:我们是怎么得到梯形面积公式的?梯形面积的研究过程与研究小数乘法、三角形面积有什么相似的地方?如果用转化的思想来研究圆的面积,你会怎么研究?让学生明确地提炼转化这条数学研究的主线。
四、在植树问题中渗透对应思想
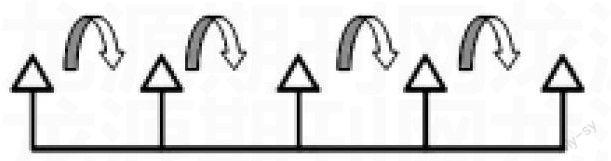
《植树问题》一课很多老师都把它分为两端都栽,只栽一端(封闭图形),两端都不栽的情况,看似清晰,但学生还是经常搞不懂什么时候加1,什么时候减1。植树问题其实主要解决间隔问题,而间隔问题的本质是对应思想。植树问题的三种情况其实就是间隔数与棵数的对应关系,我们可以用对应的数学思想统领我们的整个课堂,让学生在理解一一对应的基础上,理解各种变化的情况。
课一开始,屏幕先出示两幅图,哪一幅你能很快地看出蜜蜂和花朵一样多,为什么?(一幅图杂乱,另一幅图蜜蜂和花朵一一对应)向学生初步渗透一一对应。在自主探索过程中,老师可以再通过有意识引导间隔数与棵数之间一一对应。如两端都栽的情况:
利用直观图引导学生一眼看出1棵数对应1个间隔,最后一棵数没有间隔了。只栽一端和两端都不栽的情况也可以让学生同桌互相说一说,通过探究表格找出间隔数与棵数之间的关系。通过这样的引导,已经潜移默化地向学生渗透了一一对应的数学思想。
有效的课堂教学,并不能单纯以学生掌握了多少知识作为唯一目标,同时还要考虑我们向学生渗透了多少的数学思想,学生的可持续发展得到了多少的提高。只有把握住数学思想,才能高屋建瓴。教师要从低年级的潜意识阶段让学生似有所悟,到中年级时引导学生多次运用,把数学思想逐步明朗,最后到高年级就可以让学生运用自如,促进学生的深刻理解。教师只有提高对数学思想重要性的认识,结合不同内容、不同阶段的知识教学,有意识地向学生进行孕育和渗透,才能让数学思想之花在数学课堂怒放。
参考文献:
[1]钱守旺.教好小学数学并不难[M].北京大学出版社,2012-11.
[2]吴正宪.吴正宪课堂教学策略[M].华东师范大学出版社,2013-01.
编辑 王团兰

