预约“生成” 精彩纷呈
戴树金
【摘要】 生成性教学是指教师根据课堂中的互动状态及时地调整教学思路和教学行为的教学形态,本文力图从创设情境,课堂质疑,顺水推舟,引导总结方面对如何在数学课堂教学中实施生成性教学进行研究与探索,以培养学生的创新精神和实践能力,促进学生的可持续发展.
【关键词】 生成;教学;精彩
生成性教学是指教师根据课堂中的互动状态及时地调整教学思路和教学行为的教学形态,它作为一种新的教学方式,越来越受到广泛的关注. 生成性课堂教学强调教学是教师与学生积极互动、共同发展的过程,不只是忠实地执行课堂计划,更是师生共同开发和丰富课程的创造过程. 这就要求我们教师根据变化情况善于重组课堂教学中从学生那里涌现出的各种各样的信息,及时地将学生现实学习状态中的困惑和疑问整合形成新的教学生成点,推进教学进程在具体情境中的动态生成,从而使课堂教学多一份“精彩”,多一份生机,让学生智慧的火花贯串课堂教学的全过程. 那么,怎样才能挖掘课堂教学的生长点,使数学课堂实现有效生成呢?下面笔者就通过实例谈谈可以从以下方面进行尝试.
一、创设情境,迎接生成
生成需要一定的情境. 教师为学生创设适宜的情境,才能引起学生的学习兴趣,从而把学生引入一种渴求参与的状态. 这时,学生的思维也处于最佳状态,智慧的火花不断闪现,生成就能成为可能,也能变为现实. 例如在“有理数的乘法”这节课的教学中,可以利用电脑创设蚂蚁在数轴上运动的情境,引导学生领会有理数乘法法则的合理性,课堂练习的一名学生得出了(-3) × (-4) = 9的错误结论,教师没有简单的否定这个答案,而是接着问:“(-3) × (-4)等于多少呢?”他回答:“等于3”,其他学生都用疑惑的目光看着他,为什么这名学生会连续出现错误,于是我要求他解释怎样得到这样的结果的,他解释说:“(-3) × (-4)在数轴上,可以看作从-3这个点出发,向相反方向运动4次,每次移动3个单位,所以等于9……”听完这名学生的解释,教师敏锐地判断出他对有理数乘法法则的理解出现了偏差,没有分清楚前后两个负号的涵义,这正是本节课的难点,于是调整教学程序,组织学生讨论:刚才这名学生的回答有合理的地方吗?他错在哪里?如何帮助他纠正?学生们在激烈的讨论中总结:他合理的地方是知道乘以-4代表向相反方向运动4次,但是-3不是表示从原点左边3个单位开始运动,而是表示从原点出发每次向相反方向(右)移动4个单位……随着讨论的深入,这节课的难点让学生彻底突破了,所有学生对有理数的乘法法则都有了更加深刻的认识. 学生在课堂活动中出现的一个偶然的错误成为教师引导学生突破教学难点的突破口,教师敏锐的判断让没有预设的生成成为激发学生学习兴趣、突破教学难点的有效资源. 如果善于抓住这个契机继续下去,就会使数学课堂教学变得生动活泼、扣人心弦,起到事半功倍的教学效果.
二、課堂质疑,接纳生成
在生成的课堂中,教师应注重培养学生的批判意识,鼓励学生对知识的质疑和对教师的超越. 教学过程是师生互动发展的过程,当课堂教学过程中出现了有利于教学发展的“课堂质疑”时,教师应该针对教学实际进行灵活调整,接纳学生的生成,给学生提供充分发展的机会,让学习成为学生的一个富有个性的过程.
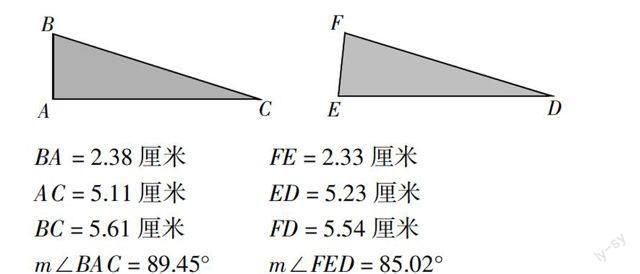
如在一次习题课上,有一道判断题:“面积和周长都相等的两个三角形是全等三角形”. 教师觉得这个问题难度不大,于是在讲评时直接告诉学生 “这个命题是错误的”. 这时有位学生小声的嘀咕:“为什么是错误的?”教师看到这个学生满脸疑虑,也想把这个问题说清楚:“周长一定的三角形形状各异 ,而这些三角形中就存在面积相等的情形. 你可以画出图形来 ……”说完又接着讲解其他题目. 过了10多分钟,这个学生还是满脸疑惑. 教师就让这个学生站起来发言,他说:“老师,我画的图形怎么都是全等的?”教师又问其他同学:“有谁画出周长和面积都相等但不全等的三角形了?”好多学生都说没有画出来. 教师准备到黑板上去画图,在转身走向讲台的时候发现这个图形很难画出来,难怪学生一脸疑虑. 经过和学生的激烈讨论,老师用几何画板作出如下图形.
周长△BAC = 13.10厘米 周长△FED = 13.10厘米
面积△BAC = 6.08厘米2 面积△FED = 6.08厘米2
BA = 2.38厘米 FE = 2.33厘米
AC = 5.11厘米 ED = 5.23厘米
BC = 5.61厘米 FD = 5.54厘米
m∠BAC = 89.45° m∠FED = 85.02°
通过课堂质疑. 学生在作图的过程中不仅体会了数形结合的数学思想,还拓展了数学思维空间,培养了独立获取新知识的能力.
三、顺水推舟,拓展生成
教学过程是师生互动发展的过程,学生不是课堂教学的配角,而是具有主观能动性的主体. 课堂教学不应该拘泥于预先设定的程序,要鼓励学生大胆超越和即兴创造. 数学教学需要预设,而精心的预设也必须通过课堂的生成才能顺利实施. 当课堂教学过程中出现了有利于教学发展的“非预设生成”时,教师应该针对教学实际进行灵活调整,顺水推舟拓展学生的生成,给学生一个自主探究、创新能力和个性发展的平台,创设积极互动的课堂学习环境.
如在“三角形全等的判定”的复习过程中,笔者作了这样的预设:
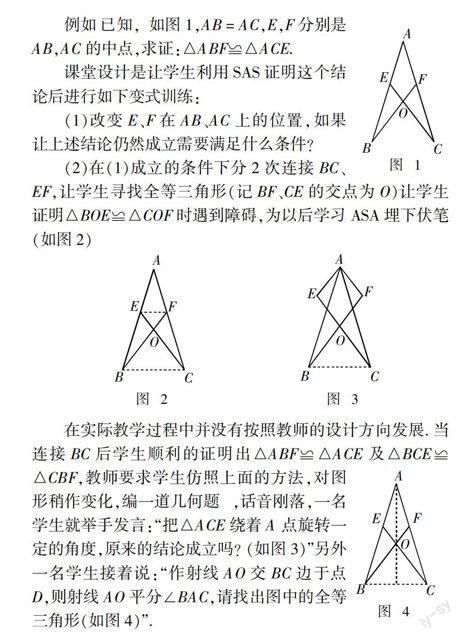
例如 已知,如图1,AB = AC,E,F分别是AB,AC的中点,求证:△ABF≌△ACE.
课堂设计是让学生利用SAS证明这个结论后进行如下变式训练:
(1)改变E、F在AB、AC上的位置,如果让上述结论仍然成立需要满足什么条件?
(2)在(1)成立的条件下分2次连接BC、EF,让学生寻找全等三角形(记BF、CE的交点为O)让学生证明△BOE≌△COF时遇到障碍,为以后学习ASA埋下伏笔(如图2)
在实际教学过程中并没有按照教师的设计方向发展. 当连接BC后学生顺利的证明出△ABF≌△ACE及△BCE≌△CBF,教师要求学生仿照上面的方法,对图形稍作变化,编一道几何题 ,话音刚落,一名学生就举手发言:“把△ACE绕着A点旋转一定的角度,原来的结论成立吗?(如图3)”另外一名学生接着说:“作射线AO交BC边于点D,则射线AO平分∠BAC,请找出图中的全等三角形(如图4)”.
学生的发散思维让教师折服,让先前的准备显得格外“单薄”,教师面对这样的生成已经无法按照原来的预设开展教学,最合理的选择就是顺水推舟,利用学生的问题拓展下去,于是问:“谁能告诉大家为什么AD平分∠BAC?”在教师的引导下,学生的思维更加活跃,马上有学生回答:“∵△BCE ≌ △CBF,∴∠OCB =∠OBC ∴ OB = OC,再利用SAS可得△ABO ≌ △ACO,所以∠BAO=∠CAO”. 另外一个学生紧接着说:“可以用SSS来证明△ABO≌△ACO……”、“老师,还能用SAS证明△AEO≌△AFO”……一节课在热烈的讨论中结束. 在课后的反思中,教师认识到数学课堂是动态生成的过程,对教学过程中因学生的思维火花而展示的“非预设生成”,教师需要积极鼓励,顺水推舟,让学生的智慧之光得以延续和拓展,真正体现以学生的发展为本的教育理念.
四、引导总结,升化生成
一节课生成的知识往往很多,怎样才能使其中有用的部分被学生真正吸收呢?这就需要教师及时加以引导总结,促进生成的知识再一次升华. 引导总结的方式很多,教师可以引导学生进行系统归纳,从中提炼学习方法,也可以对已生成的内容再做进一步的生成发展,还可以引导学生通过反思去矫正已生成的内容.
总之,在开放的课堂中,教师要正确面对学生突如其来的、个性化的思维亮点,巧妙地将“生成”与“预设”融合起来,通过智慧的碰撞,创设生动的、自主的、合作的、创造的、充满活力的智慧课堂. 让学生的潜能在活动参与中得以发挥,在体验中快乐成长,在生成性教学中得到充分的发展.