基于分数阶傅里叶变换的Chirp浅剖精细探测方法

朱建军魏玉阔杜伟东李海森*

①(哈尔滨工程大学水声技术重点实验室 哈尔滨 150001)

②(哈尔滨工程大学水声工程学院 哈尔滨 150001)

基于分数阶傅里叶变换的Chirp浅剖精细探测方法

朱建军①②魏玉阔①②杜伟东②李海森*①②

①(哈尔滨工程大学水声技术重点实验室 哈尔滨 150001)

②(哈尔滨工程大学水声工程学院 哈尔滨 150001)

实现弱回波信号检测和高信噪比(SNR)浅剖图像获取是浅剖精细探测的首要任务。该文在分析分数阶傅里叶变换(FrFT)解卷积原理，推导时间量纲化变换公式的基础上，提出一种基于FrFT的浅剖精细探测新方法。该方法通过FrFT解卷积实现分数阶傅里叶域(u域)沉积层冲激响应求解，采用u域加窗滤波技术对带内噪声进行有效抑制，经时间量纲化变换实现高信噪比u域沉积层冲激响应包络信号至时域浅剖包迹的直接变换，得到高质量的浅剖图像。仿真实验和实测数据处理验证了算法的精细探测能力，算法性能优于脉冲压缩和自回归(AR)预测滤波方法。

信号处理；浅地层剖面；精细探测；分数阶傅里叶变换；带内噪声抑制；时间量纲化变换

1 引言

海底浅地层剖面探测(简称浅剖探测)的精细程度直接关系着海底科学考察的有效性、沉积层结构分析的合理性和遥测参数获取的准确性[1]。目前，浅剖探测广泛采用基于脉冲压缩技术的Chirp声呐探测方法[2,3]，同时也将解卷积技术用于信号处理[4]。但上述技术方法在进行浅剖探测时存在以下问题：首先，脉冲压缩子波通常存在较高的旁瓣，当子波旁瓣与弱子波主瓣幅度相当时会产生子波遮蔽效应，造成地层误判和漏判。虽然采用探测信号加窗法可抑制脉冲压缩子波的旁瓣[5]，但窗函数会减弱信号能量、减小信号有效带宽，降低探测分辨率和探测深度。其次，在不损失分辨率的前提下有效抑制带内噪声困难。传统去噪方法通常具有滤波的性质，在滤除噪声的同时会损失信号带宽，导致分辨率下降。特别是在对宽带信号处理时，传统带通滤波技术难以滤除带内噪声干扰[6]，而带内噪声的存在会影响对弱回波信号的检测，限制系统探测性能和浅剖成图质量的进一步提高。最后，解卷积处理需要在较高信噪比下才具有良好的处理性能[7,8]，低信噪比时实现精细探测困难。

由于Chirp信号在最优阶分数阶傅里叶u域上具有最佳的能量聚集性[9]，而噪声仍均匀分布于几乎整个分数阶傅里叶域[10]。基于这一优越处理性能，本文提出一种基于分数阶傅里叶变换(Fractional Fourier Transform, FrFT)技术的Chirp浅剖精细探测方法，通过FrFT解卷积、u域加窗滤波和时间量纲化变换，在u域实现高信噪比浅剖图像的获取和浅地层剖面的更精细探测，达到传统时域或频域方法均无法获得的处理效果，仿真实验和实测数据处理验证了方法的有效性。

2 浅剖回波信号模型

在不考虑水声信道时散和多普勒效应的情况下，浅剖回波信号可表示为[11]

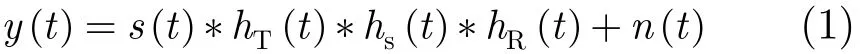
其中，s(t)为探测信号，hT(t)为发射换能器冲激响应，hs(t)为海底浅地层冲激响应，hR(t)为接收换能器冲激响应，n(t)为高斯白噪声。通常换能器均经过校准，因此可将式(1)简化表示为探测信号与沉积层冲激响应卷积的形式：式(2)中M为沉积层反射界面的个数am和τm分别为第m反射界面的回波信号幅度和时延。

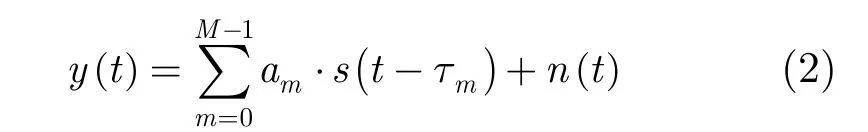
3 基于FrFT的浅剖精细探测算法

3.1 u域解卷积原理

信号的FrFT可理解为时域信号在时频平面上逆时针旋转α角度的u域表示，当旋转至αopt= arctan(Δk)+π/2时, Chirp信号会变为冲击信号而出现最佳能量聚集，此时的FrFT称为最优阶FrFT，变换阶数popt=2/π称为最优变换阶数[12]。FrFT以量纲归一化理论为基础建立算法模型，参量均为量纲归一化量(无量纲量)，如∇k=∇B/∇T=kS2, ∇B, ∇T 和S=sqrt(T/fs)分别为量纲归一化的频率变化率、带宽、脉冲宽度和时间因子，符号“∇”表示量纲归一化。

由FrFT公式及其运算性质[13,14]，推得Chirp信号关于角度的FrFT为

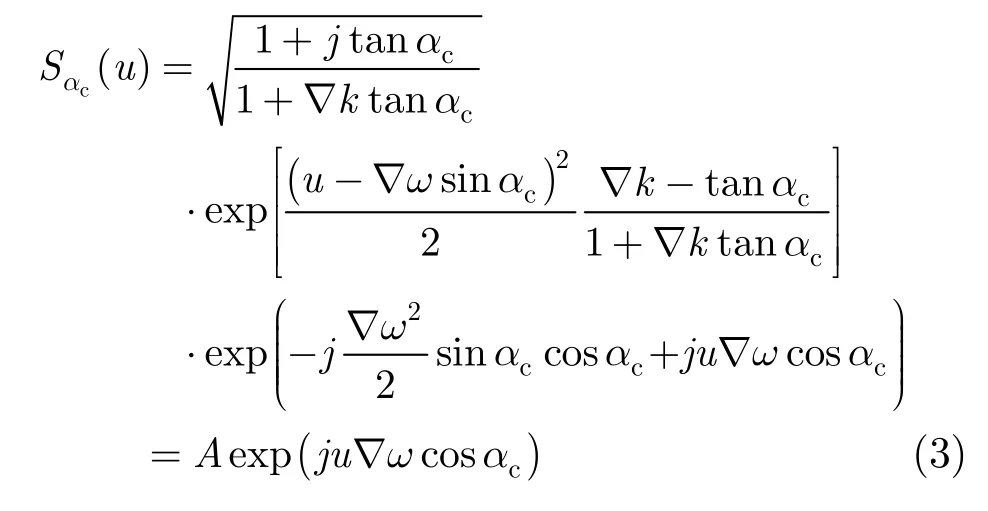
式中A为常量。由FrFT的阶数可加性，最优阶FrFT可分解为αc和π/2两个角度的顺序逆时针旋转，而π/2角度坐标轴的逆时针旋转等价于傅里叶变换[15]，因此信号s(t)的最优阶FrFT又可表示为Sαc(u)的傅里叶变换：

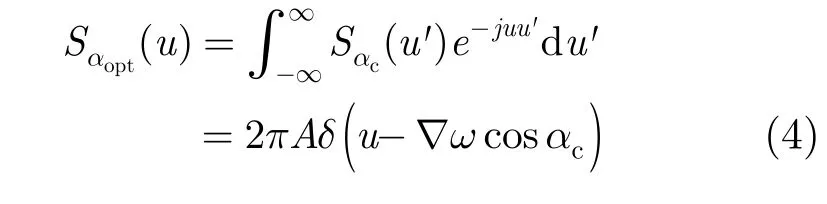
经最优阶FrFT变换，M个浅剖回波信号转变为M个u域上的冲击信号，实现了浅剖信号的u域解卷积处理，得到了沉积层冲激响应的u域表示(下文称u域沉积层冲激响应)，u域解卷积原理如图1所示，T为时间窗长度，Ui为Chirp信号的u域分布位置。

实际信号处理时，时间窗长度T是有限的，因此式(5)的积分区间实际为[-∇T/2, ∇T/2]，从而浅剖信号最优阶FrFT应表示为sinc函数的形式：

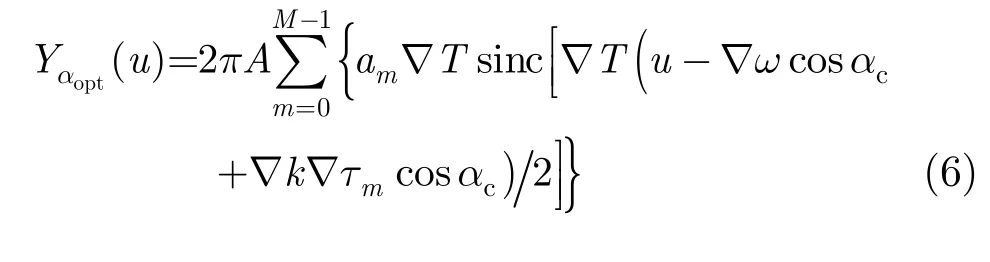
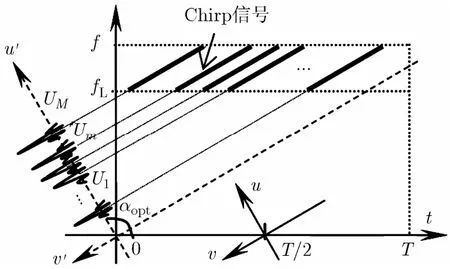
图1 u域解卷积原理

3.2 u域加窗滤波处理

由于Chirp信号为宽带信号，因此带内信号与噪声在时频域上是完全耦合的，采用传统带通滤波方法不能消除带内噪声干扰，而浅剖信号经最优阶FrFT后信号能量主要集中在sinc信号主瓣范围内，高斯白噪声则分布于几乎整个u域上，这一过程将耦合区域由整个频带缩小至sinc信号主瓣宽度以内，有效实现了信号与噪声的去耦。从而以u域浅地层冲激响应峰值位置为中心设计窄带滤波器H(u)，可有效滤除带内噪声干扰。FrFT为线性变换，因此u域滤波过程可表述为

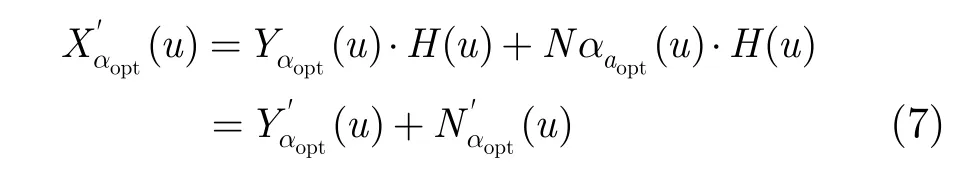
其中H(u)为幅度归一化u域滤波器响应。以NH表示滤波器宽度(通常取奇数)，则滤波输出信噪比为

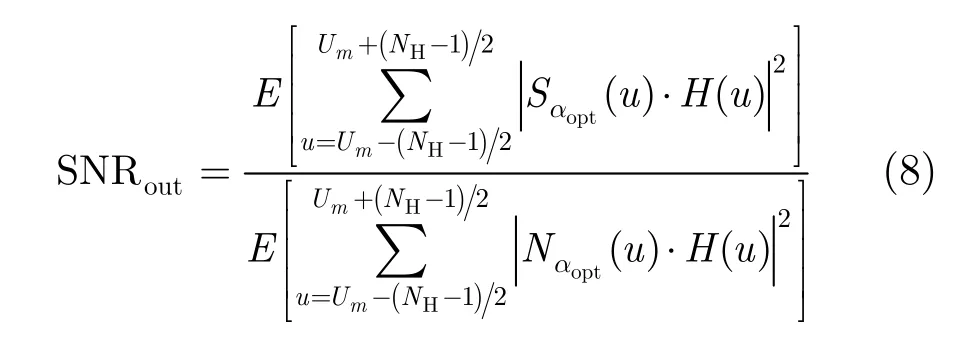
经分析发现，选择合适的滤波器窗函数在有效滤除带内噪声、最大化输出信噪比的同时可对冲激响应的旁瓣进行有效抑制，降低高能量信号旁瓣对低能量信号的遮蔽影响，提高弱信号检测能力。首先，针对4种典型窗函数进行研究，分析相同窗宽下不同窗函数对噪声的抑制效果，见图2。由于具有宽主瓣和低旁瓣等特性，布莱克曼(blackman)窗噪声抑制效果最好，较矩形窗输出信噪比可提高3.8 dB，后续将采用blackman窗设计u域滤波器。

另外，窗宽是影响冲激响应旁瓣抑制效果的另一个主要因素，不同宽度的blackman窗对旁瓣的抑制效果如图3所示。对比发现，当窗宽与sinc信号主瓣宽度相当时(主瓣宽度为17个样本点)，可抑制掉几乎所有的旁瓣，同时保留了绝大部分的信号能量。

3.3 浅剖包迹获取

时频平面α角度的逆时针旋转可将N点时域Chirp信号变为N点u域信号，因此u域信号各样本点与时域信号各样本点间必然存在一一映射关系，从而u域样本序列可通过某一变换关系得到与之对应的时域样本序列。从量纲归一化理论出发，将无量纲u值至时域时间量纲量的变换称为时间量纲化变换。浅剖包迹是时域沉积层冲激响应的包络，在获得高信噪比u域沉积层冲激响应的前提下，通过时间量纲化变换可实现高信噪比浅剖包迹的获取，从而最终得到高信噪比的浅剖图像。首先，由式(6)得到浅剖信号幅度可表示为

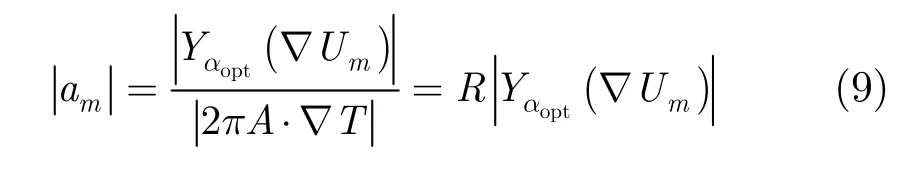
即u域沉积层冲激响应幅度与时域沉积层冲激响应的幅度间存在一一对应的等比例关系，比例系数为常数R。其次，由量纲归一化理论及Chirp信号在时频域和u域分布的几何关系，推得时延为τm的沉积层回波信号在u域的分布位置(或冲激响应峰值位置)为式中fL为Chirp信号起始频率。为了便于分析，以u轴起始点为零点，则u域各样本点对应的索引号为

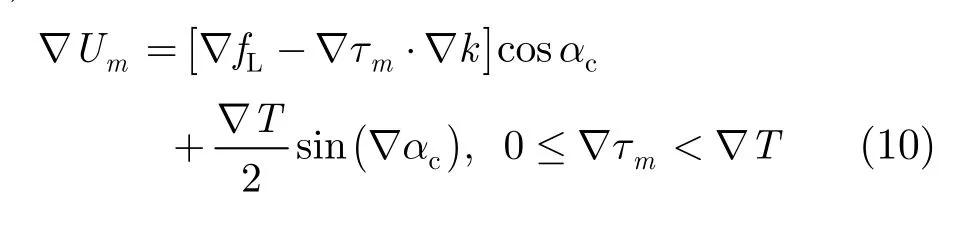
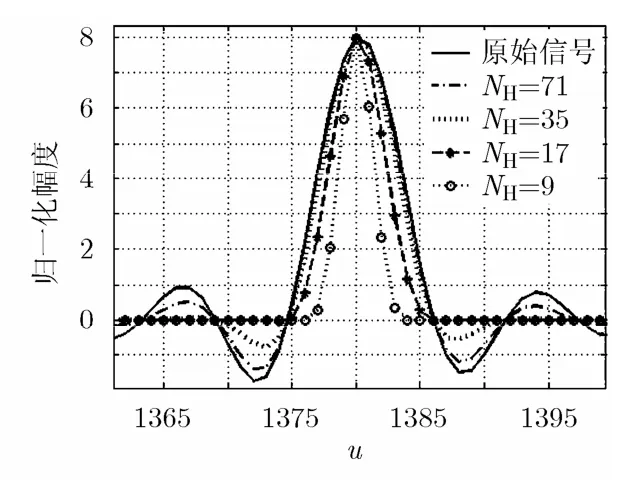
图3 滤波器宽度对旁瓣的抑制效果

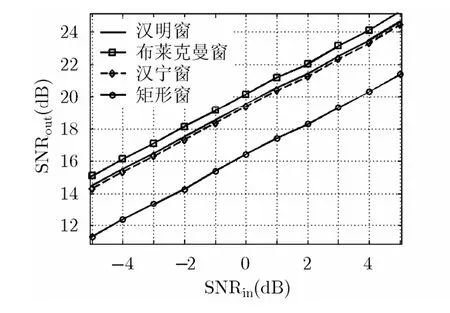
图2 不同窗函数时u域滤波输出SNR

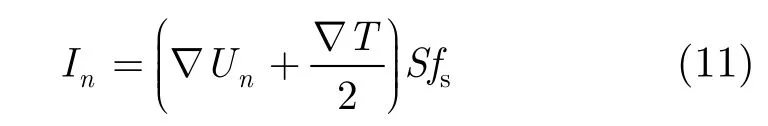
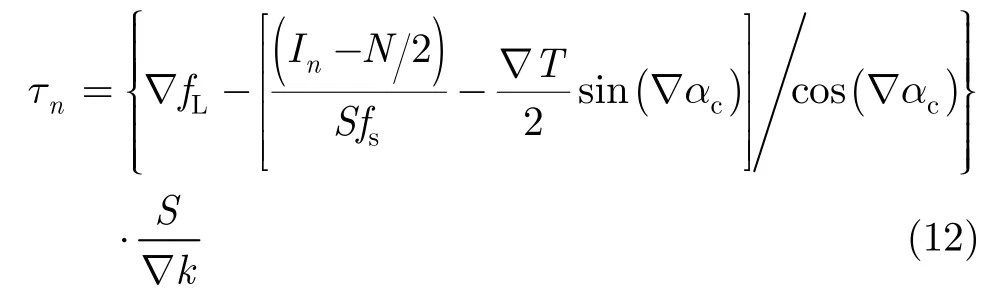
其中，n∈[1,2,…,N]。上式给出了u域样本序列与时域样本序列间的映射关系，该式实现了u值的时间量纲化变换。

由图1几何关系和式(12)易知，时间量纲化引入了一个时间偏移量ζoffset，该偏移量产生原理如图4所示，图中粗虚线表示0时延Chirp信号，其u域分布位置与时域时延相对应，而u轴上大于该位置的区域与时域 [-ζoffset, 0)相对应。由式(12)也可推得ζoffset为

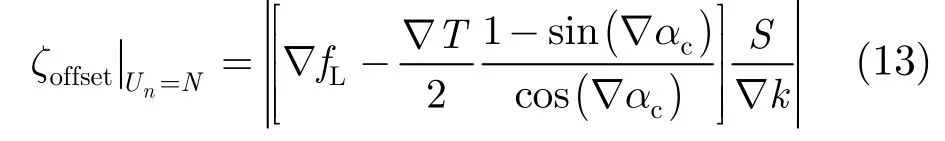
由式(13)易知，时间偏移量仅与Chirp信号的下限频率、调斜率、时间窗长度以及采样频率有关，与信号时延无关。因此，时间偏移量可直接计算得到而不受时延信息的影响。

从而时间量纲化得到时域样本点无偏移的时延值应为

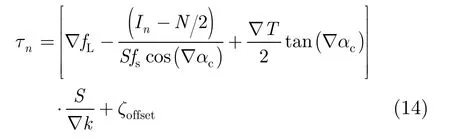
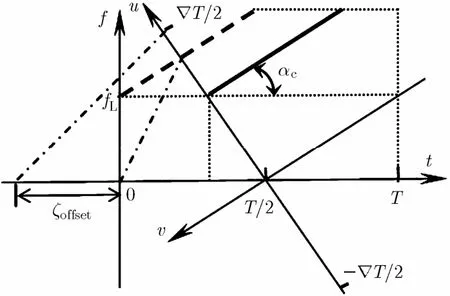
图4 时间偏移量产生原理

由式(14)可得到u域相邻样本点在时域上间隔的样本点数为

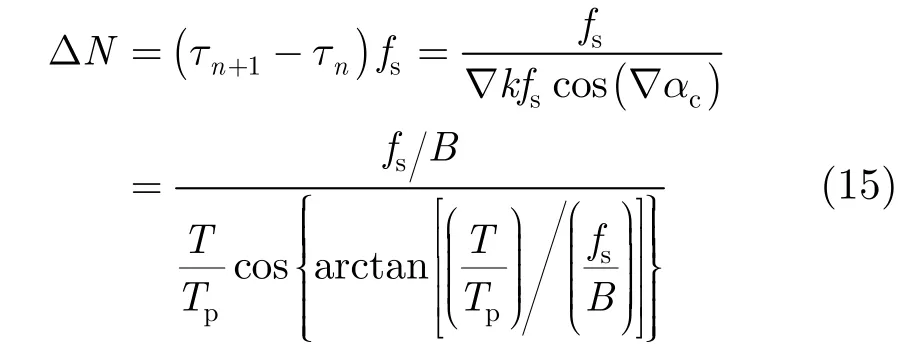
其中Tp为发射信号脉宽。当ΔN为整数时，时间量纲化得到的时域样本序列具有“插值”的特性(ΔN为插值点数)，因此，通过对该序列做ΔN倍“抽取”和低通滤波即可得到浅剖包迹。综上，求解浅剖包迹|hs(n)|的过程可表述为

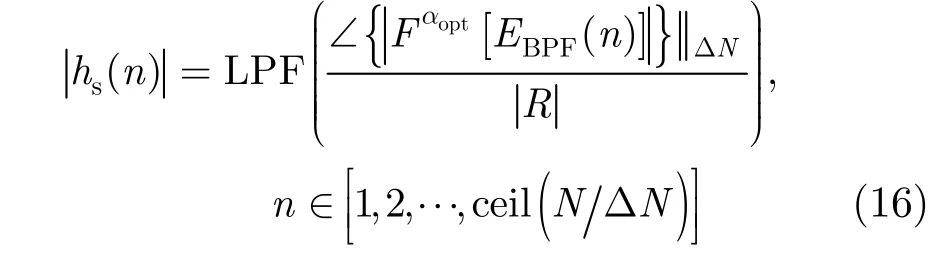
其中，EBPF(n)为带通滤波输出回波信号，“Fα”表示p=2α/ π阶FrFT“，∠”表示u值的时间量纲化，“||ΔN”表示ΔN倍抽取，LPF表示低通滤波，ceil(N/ΔN)为向趋近于正无穷取整。基于这一求解过程提出了基于FrFT的Chirp浅剖精细探测算法，算法流程如图5所示。由于浅剖探测为主动声呐探测，通常已知探测信号参数，但当考虑多普勒效应时，也可对实际回波信号参数进行估计以用于算法计算；同时，通过u域冲激响应包络峰值搜索还可对浅地层回波信号的幅度和时延信息进行估计。

4 算法仿真及数据处理分析

4.1 计算机仿真实验

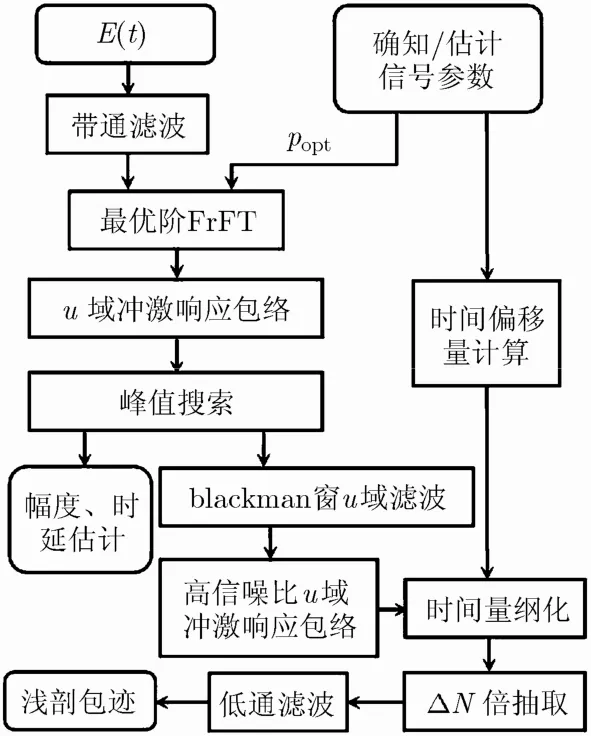
图5 浅剖精细探测算法流程图

采用文献[16]提出的非等厚沉积层分层模型(层数可是任意值)，利用式(2)设计浅剖回波信号，通过与脉冲压缩法和文献[17]提出的自回归(AutoRegressive, AR)预测滤波方法进行比对，对该算法性能进行验证。这里取11层不同厚度的沉积层，由于各层反射强度具有随机性，回波信号幅度均匀随机产生，相应的回波时延及归一化反射强度分别为τ=[3.0, 7.0, 9.5, 11.8, 14.2, 16.0, 18.0, 21.0, 23.0, 25.5, 28.0] ms, a=[1.00, -0.42, 0.67, 0.33, -0.50, 0.25, 0.34, 0.28, -0.50, -0.37, 0.25]。发射信号为脉宽6 ms、频率2～6 kHz的Chirp信号，信噪比6 dB，观测时间窗长度36 ms。由式(15)计算时间量纲化后采用2倍抽取(ΔN=2)，则fs=41.56 kHz。

实验1 将带通滤波输出浅剖信号做最优阶(1.33318阶)FrFT变换，得到u域沉积层冲激响应并进行u域加窗滤波处理，blackman窗宽为15点，滤波效果如图6所示，滤波结果表明：u域解卷积和加窗滤波在有效滤除带内噪声的同时对冲激响应旁瓣进行了有效抑制。由式(13)计算时间偏移量为15.025 ms，对图6中高信噪比的u域沉积层冲激响应包络进行时间量纲化变换，经2倍抽取和低通滤波得到了高信噪比的浅剖包迹信号，如图7所示，与脉冲压缩方法相比，本文算法输出时域波形具有更低的旁瓣和更高的信噪比，且精确探测到了不同反射强度的沉积层。

同时，采用AR预测滤波方法对同一组信号进行处理，处理结果见图8，由于AR预测滤波基于传统的解卷积方法，对噪声干扰较敏感，虽能探测到主要的浅地层信息，但带内噪声干扰仍较严重。仿真实验从u域和时域上均表明本文算法对带内噪声和冲激响应旁瓣的抑制效果，直观地反映了其优于脉冲压缩和AR预测滤波方法的浅剖精细探测能力。

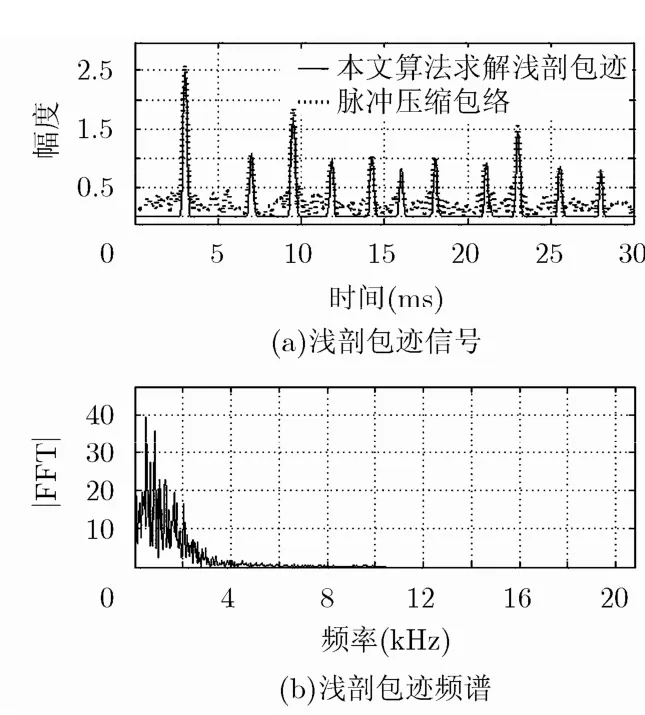
图7 浅剖包迹信号及其频谱

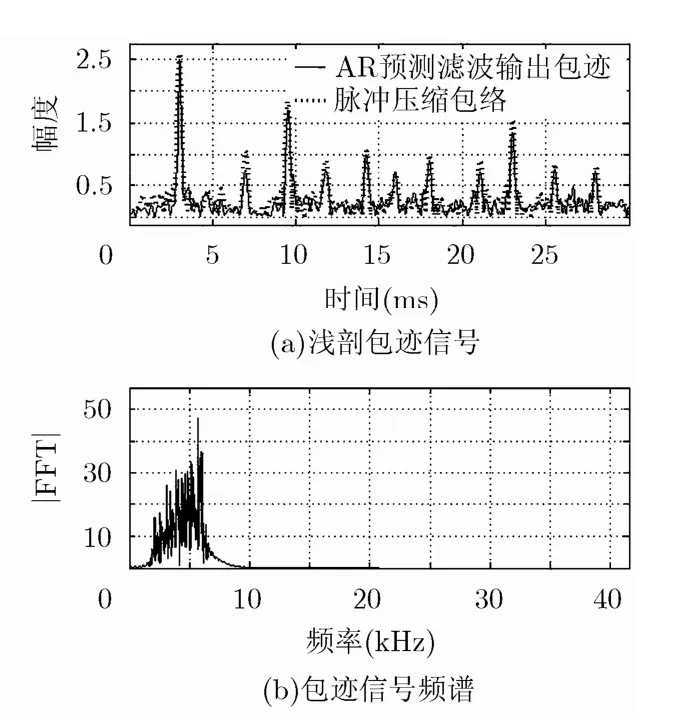
图8 AR预测滤波输出浅剖包迹及其频谱

实验2 输入信噪比为-10～10 dB时，采用Monte Carlo方法算法输出信噪比进行5000次统计实验，实验结果见图9。由于有效抑制了带内噪声干扰，本文算法输出信噪比最高，与脉冲压缩法相比，在低于0 dB的输入信噪比时可获得10 dB左右的增益。带内噪声的有效抑制有利于对弱回波信号的检测，从而有利于获得更精细的浅地层剖面图像。

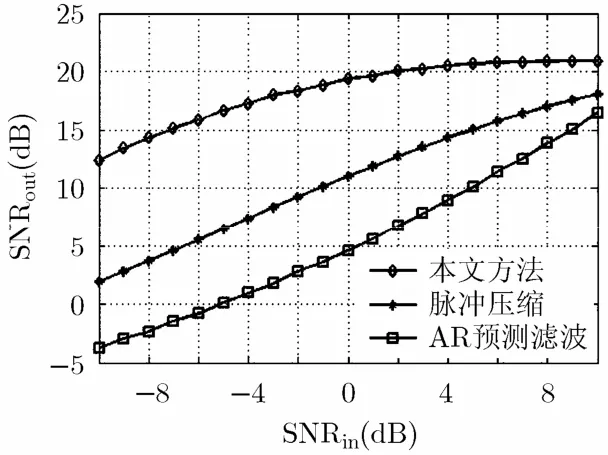
图9 输出信噪比变化曲线

4.2 数据处理分析

采用两组Chirp浅剖原始数据对算法性能进行验证，Chirp探测信号频率范围2～6 kHz，脉宽32 ms，采样频率26.316 kHz，处理结果如图10和图11所示。

图10是存在斜坡和沟壑等复杂地形的沉积层剖面处理结果。结果表明，本文算法可以有效地检测到斜坡地形的弱回波信号(图中实线框区域)，虽然AR预测滤波法也检测到了弱回波信号，但背景噪声明显高于本文算法，浅剖图像图10(c)较图10(a)和图10(b)更加清晰，细微地形更加丰富，充分说明了算法对带内噪声较强的抑制能力。

图11是对多层沉积层的探测结果，脉冲压缩法和AR预测滤波法仅能探测到海底以下20 m左右的地层结构，无法探测更深的沉积层结构特征。图11(c)中不仅清晰地探测到了海底以下20 m区域的沉积层，而且还探测到了100 m深度的弱回波信号，同时整个探测结果的背景噪声干扰抑制效果明显，浅剖图像更加清晰，计算其信噪比比图11(a)和图11(b)分别提高了约7.2 dB和8.4 dB。为了更加直观地说明本文算法处理性能，随机选取第495个探测周期的数据采用上述3种方法进行处理，处理结果如图12至图14所示，时域波形及浅剖包迹处理结果均表明了本文算法的噪声抑制效果以及地层的精细探测能力，特别实现了100 m深度处弱回波信号的检测。数据2的处理结果再次验证了本文算法优于其它两种方法的处理性能。

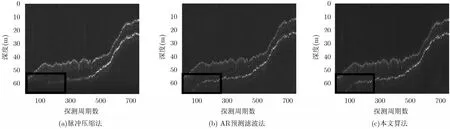
图10 数据1处理结果

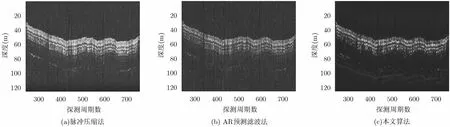
图11 数据2处理结果

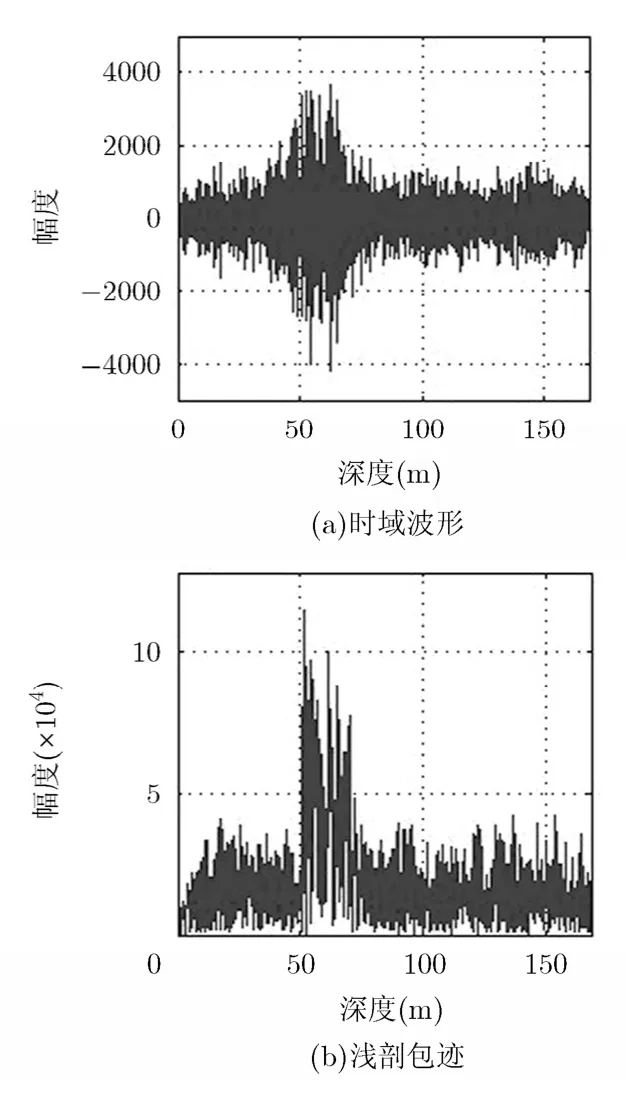
图13 AR预测滤波处理结果

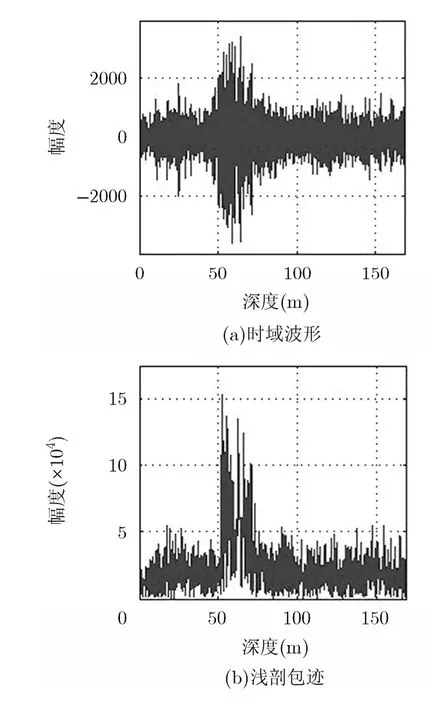
图12 脉冲压缩处理结果

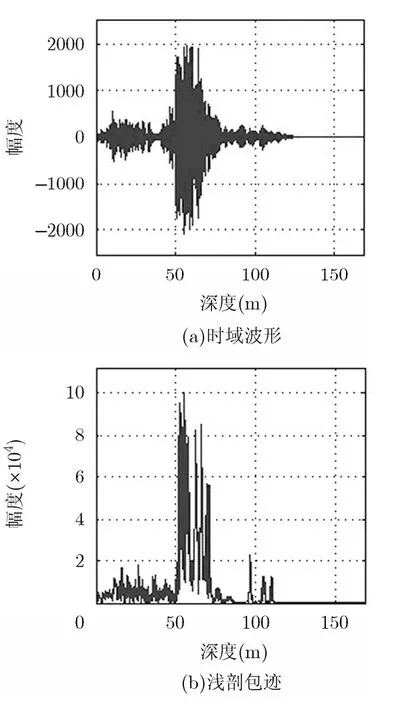
图14 本文算法处理结果

5 结束语

本文在对FrFT解卷积原理、u域加窗滤波以及时间量纲化理论研究的基础上，提出了一种基于FrFT的Chirp浅剖精细探测新方法，该方法在u域实现海底浅地层的解卷积和滤波处理，具有优于传统方法的带内信号与噪声的去耦与滤波效果，从而具有更高的信噪比增益以及对微弱地层回波信号的检测能力，时间量纲化变换将高信噪比的u域沉积层冲激响应包络变换至时域，直接得到了高信噪比的浅剖包迹，并且由于u域加窗滤波处理，本文算法输出浅剖包迹较脉冲压缩输出冲击信号具有更强的旁瓣抑制能力。计算机仿真和实验数据处理验证了该方法优于脉冲压缩和AR预测滤波方法，为浅地层剖面精细探测提供了新的技术途径。

[1] Gron O and Boldreel L O. Sub-bottom profiling for large-scale maritime archaeological survey[C]. Proceedings of Oceans 2013 Marine Technology Society, Bergen, Norway, 2013: 1-8.

[2] Sandrine R, Michel L, Rozenn D, et al.. Forward modeling for marine sediment characterization using chirp sonars[J]. Geophysics, 2011, 76(4): 91-99.

[3] Tseng Yao-ting, Ding Jian-jun, and Liu Char-shine. Analysis of attenuation measurements in ocean sediments using normal incidence chirp sonar[J]. IEEE Journal of Oceanic Engineering, 2012, 37(3): 533-543.

[4] Xie Yu-jiang and Liu Gao. Predicting the distribution of reservoirs by combining variable wavelet model of seismograms with wavelet edge analysis and modeling[J]. Journal of Applied Acoustics, 2014, 101: 116-123.

[5] Hakan K and Derman D. A procedure to reduce side lobes of reflection wavelets: a contribution to low frequency information[J]. Journal of Applied Geophysics, 2013, 96: 107-118.

[6] 齐林, 陶然, 周思永, 等. 基于分数阶傅里叶变换的线性调频信号的自适应时频滤波[J]. 兵工学报, 2003, 24(4): 499-503. Qi Lin, Tao Ran, Zhou Si-yong, et al.. An adaptive time-frequency filtering method based on fractional Fourier transform for linear frequency modulation signals[J]. Acta Armamentarii, 2003, 24(4): 499-503.

[7] Hakan K. Further improvement of temporal resolution of seismic data by autoregressive (AR) spectral extrapolation[J]. Journal of Applied Geophysics, 2006, 59(4): 324-336.

[8] Zeng Wen-jun, Jiang Xue, Li Xi-lin, et al. Deconvolution of sparse underwater acoustic multipath channel with a large time-delay spread[J]. The Journal of the Acoustical Society of America, 2010, 127(2): 909-919.

[9] 朱健东, 赵拥军, 唐江. 线性调频连续波信号的周期分数阶Fourier变换检测与估计[J]. 电子与信息学报, 2013, 35(8): 1827-1833. Zhu Jian-dong, Zhao Yong-jun, and Tang Jiang. Periodic FRFT based detection and estimation for LFMCW signal[J]. Journal of Electronics & Information Technology, 2013, 35(8): 1827-1833.

[10] 陈鹏, 侯朝焕, 马晓川, 等. 基于匹配滤波和离散分数阶傅里叶变换的水下动目标LFM回波联合检测[J]. 电子与信息学报, 2007, 29(10): 2305-2308. Chen Peng, Hou Chao-huan, Ma Xiao-chuan, et al.. The joint detection to underwater moving target’s LFM echo based on matched filter and discrete fractional fourier transform[J]. Journal of Electronics & Information Technology, 2007, 29(10): 2305-2308.

[11] Carcreff E, Bourguignon S, Idier J, et al.. Including frequency-dependent attenuation for the deconvolution of ultrasonic signals[C]. Proceedings of Meetings on Acoustics, Montreal, Canada, 2013, 19: 1-9.

[12] 仇兆炀, 陈蓉, 汪一鸣. 基于FRFT的线性调频信号欠采样快速检测方法[J]. 电子学报, 2012, 40(11): 2165-2170. Qiu Zhao-yang, Chen Rong, and Wang Yi-ming. Fast detection of LFM signal based on FRFT and sub-Nyquist sampling[J]. Acta Electronical Sinica, 2012, 40(11): 2165-2170.

[13] 李丽, 邱天爽. 基于分数阶傅里叶变换的双基地雷达线调频信号的参数联合估计新方法[J]. 电子与信息学报, 2012, 34(4): 878-884. Li Li and Qiu Tian-shuang. A novel method for joint parameter estimation of LFM signals in bistatic MIMO radar system on FRFT[J]. Journal of Electronics & Information Technology, 2012, 34(4): 878-884.

[14] Khalid H M and David K P. Geophysical signal parameterization and filtering using the fractional Fourier transform[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(3): 845-852.

[15] 阮航, 吴彦鸿, 叶伟. 基于FRFT-CLEAN的机动目标逆合成孔径激光雷达成像算法[J]. 电子与信息学报, 2013, 35(7): 1540-1546. Ruan Hang, Wu Yan-hong, and Ye Wei. Inverse synthetic aperture radar imaging algorithm for maneuvering target based on FRFT-CLEAN[J]. Journal of Electronics & Information Technology, 2013, 35(7): 1540-1546.

[16] Quinquis A and Radoi E. FM pulses separation for improving sub-bottom attenuation estimation[C]. Proceedings of Oceans’97, Halifax, Canada, 1997, 2: 1359-1365.

[17] Satchidananda P. Remote acoustic evaluation of seafloor sediment properties[D]. [Ph.D. dissertation], University of Rhode Island, 1992.

朱建军： 男，1981年生，助教，博士生，研究方向为海洋工程信息系统、水声信号处理.

魏玉阔： 男，1982年生，讲师，博士，研究方向为海洋工程信息系统、水声工程.

杜伟东： 男，1984年生，博士生，研究方向为海洋工程信息系统.

Chirp Sub-bottom Profiling Detailed Detection Method Based on Fractional Fourier Transform

Zhu Jian-jun①②Wei Yu-kuo①②Du Wei-dong②Li Hai-sen①②①( Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China)
②(College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China)

Weak signal detection and high SNR seismic image generation are primary tasks in detailed sub-bottom profile detection. After analyzing the principle of deconvolution based on Fractional Fourier Transform (FrFT) and deriving the formula of time dimensional transformation, a new detailed sub-bottom profile detection algorithm based on FrFT is proposed. The fractional Fourier domain (u domain) sub-bottom impulse response is achieved by u domain deconvolution and the intraband SNR is increased by u domain windowed filtering technique, then high SNR envelop of u domain sediment impulse response envelop is transformed to time domain by time dimensional transformation to get high quality sub-bottom profile. Simulation and experimental data processing validate the validity of the algorithm in intraband denoising and detailed detection, and its performance is better than pulse compression and AutoRegressive (AR) forecast filtering.

Signal processing; Sub-bottom profile; Detailed detection; Fractional Fourier Transform (FrFT); Intraband denoising; Time dimensional transform

TN911.7

A

1009-5896(2015)01-0103-07

10.11999/JEIT140140

2014-01-21收到，2014-04-15改回

国家国际科技合作项目(2008DFR70320)，国家自然科学基金(41327004, 41306182, 61401112)， 教 育 部 博 士 点 基 金(20112304130003)和哈尔滨市科技攻关项目(2008AA2AE005)资助课题

*通信作者：李海森 hsenli@126.com