角度信息辅助的集中式多传感器多假设跟踪算法
王 欢孙进平 付锦斌 毛士艺
(北京航空航天大学电子信息工程学院 北京 100191)
角度信息辅助的集中式多传感器多假设跟踪算法
王 欢*孙进平 付锦斌 毛士艺
(北京航空航天大学电子信息工程学院 北京 100191)
对于密集杂波环境中的多目标跟踪,传统集中式多传感器多假设跟踪(CMS-MHT)算法在每一时刻的航迹-量测关联假设数量大大增加,导致数据关联不确定性增大,以至很难由常规航迹得分给出正确关联,表现为高的漏情率以及航迹分裂现象。基于传感器测量误差较小时虚警与目标量测的空间分布特点,针对多个相同类型传感器进行目标跟踪,该文提出一种角度信息辅助的CMS-MHT算法,设计了新的角度信息辅助的航迹得分计算方法,可以降低航迹-量测关联的不确定性,从而得到比传统CMS-MHT更优的关联假设。仿真实验结果表明,在密集杂波环境中,该算法能有效降低漏情率,并有更好的航迹完整性。
多目标跟踪;多假设跟踪;多传感器;集中式;角度信息
1 引言
依据信息流通形式及对信息的综合处理层次,多传感器数据融合目标跟踪系统的处理结构主要有3种类型[1- 4]:集中式、分布式和混合式。集中式是将所有传感器的量测数据直接传送至一个中心处理器,由其形成统一的系统航迹,信息损失量最小,可以避免分布式结构在关联和融合各局部航迹时所遇到的困难。当前应用于集中式多传感器多目标跟踪的数据关联算法,主要是由单传感器多目标跟踪算法推广而来的。例如集中式多传感器联合概率数据互联算法(Centralized Multi-Sensor JointProbabilistic Data Association, CMS-JPDA)[5- 8]、集中式多传感器多假设跟踪算法(Centralized Multi-Sensor Multiple Hypothesis Tracking, CMS-MHT)[9- 13]等。
多假设跟踪(Multiple Hypothesis Tracking, MHT)算法可以将多目标跟踪所涉及的航迹起始、数据关联、航迹维持及航迹终止等多个环节统一在一个框架内,在检测概率比较低、杂波密度比较大和目标比较密集时,MHT算法被普遍认为是解决数据关联问题的最好方法。尽管CMS-MHT算法具有同样的优点,但在密集杂波环境下,由于每个时刻需要处理来自多个传感器的量测,与应用于单传感器的MHT算法相比,CMS-MHT处理中可能的航迹-量测关联假设数量大大增加,从而增大了航迹-量测关联假设不确定性。而航迹-量测关联假设不确定性的增加容易引发错误关联现象,最终导致得到的航迹质量降低。针对此问题,本文提出了一种改进的CMS-MHT算法,用于多个相同类型传感器的融合目标跟踪,基于虚警与目标量测的空间分布特点设计了新的角度信息辅助的航迹得分计算方法,在传感器测量误差较小时,可以得出更符合实际情况的航迹分值,进而降低了航迹-量测关联假设不确定性,提高了航迹的质量。通过比较跟踪性能的多个评估指标,仿真结果表明在密集杂波环境中,新的算法可以获得比传统CMS-MHT算法更好的跟踪效果,主要体现在降低了漏情率,同时提高了航迹完整性。
2 算法流程及滤波模型
角度信息辅助的CMS-MHT算法处理流程如图1所示。跟踪处理的框架类似于文献[11]提出的面向航迹的结构化分支MHT。在每一跟踪时刻,首先要对现有的航迹进行预测;当所有传感器的量测数据到达融合中心后,对现有航迹树增长可能的叶子结点,即形成当前时刻的航迹-量测关联假设,同时计算角度信息辅助的航迹得分;当完成航迹得分计算后,进行基于得分的航迹删除和确认;对幸存的航迹进行分簇,然后在每个簇中独立地进行k最优全局假设的生成、航迹全局概率的计算;接下来进行基于最优全局假设的N回扫剪枝;对于在N回扫剪枝后幸存的航迹进行基于全局概率的航迹删除;最后,根据当前时刻量测-航迹关联进行多传感器滤波。如果需要反馈当前的跟踪信息,则把当前时刻最优全局假设中的航迹反馈给各传感器,然后继续下一时刻的跟踪处理。航迹的起始、确认及终止处理与常规CMS-MHT相同。

图1 角度信息辅助的CMS-MHT算法处理流程
假定状态描述和量测描述均是在直角坐标系下,离散时间系统的动态方程为

其中X(k)是k时刻目标的状态向量;F(k)为目标状态转移矩阵; V(k)为零均值白色高斯过程噪声序列,协方差为Q(k)。当Ns个传感器观测同一运动目标时,第i个传感器的测量方程为
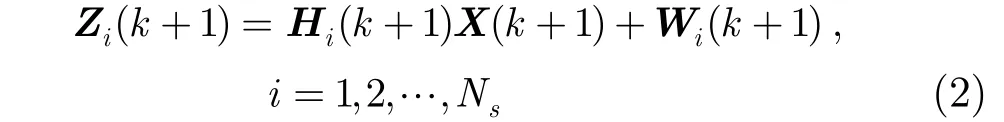
式中,Zi(k+1)为量测向量,Hi(k+1)为测量矩阵,Wi(k+1)是均值为零且相互独立的高斯序列,其协方差为Ri(k+1)。假设各个传感器独立工作,且Wi(k ), Wj(k)(i≠j), V(k)和目标初始状态相互独立。
本文采用并行滤波方法[14]。首先将所有传感器的量测集中起来,形成一个更高维的量测矢量

于是可以得到广义量测方程:
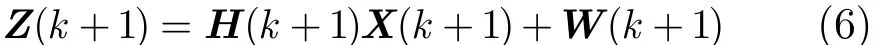
以式(1)为目标运动的状态方程,以式(6)为融合中心的广义量测方程,设k时刻目标状态的融合估计为X(k),状态协方差为P(k),则融合中心k+1时刻状态预测及状态协方差预测为

k+1时刻状态更新及状态协方差更新为

3 角度信息辅助的航迹得分计算方法
设用于跟踪的传感器数目为Ns, k时刻来自传感器i, i=1,2,…,Ns的量测数为mki,融合中心在k时刻所获最新综合量测集为ℤ(k),即

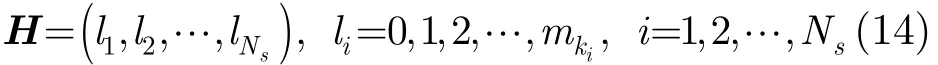
其中,当li≠0,i=1,2,…,Ns时,表示传感器i的第li个量测来自目标t;当li=0,i=1,2,…,Ns时,表示传感器i没有探测到目标t。
在传统CMS-MHT算法中,计算航迹得分时只考虑了传感器量测相对航迹t在量测空间的预测位置的分布,只使用了传感器量测与航迹t的预测位置之间的距离信息。实际当各传感器测量误差比较小时,来自目标t的各传感器量测相对目标实际位置的分布会相对集中,而虚警量测的分布是随机的。图2给出了k时刻航迹t与3个传感器量测位置关系的示例,图2(a)表示关联假设(1,1,1)对应的航迹-量测位置关系,图2(b)表示关联假设(2,2,2)对应的航迹-量测位置关系,其中Z(k)为航迹t在k时刻的量测空间预测位置,ZT(k)为航迹t在k时刻的实际位置。假定每个传感器的第1个量测、第2个量测与航迹t预测位置Z(k)的距离相同。对于关联假设(1,1,1),量测均落入航迹t的关联门内,但是量测相对目标实际位置的分布比较分散。对于关联假设(2,2,2),量测也均在关联门内,但是量测相对目标实际位置的分布比较集中。显然,当传感器测量误差比较小时,量测均来自目标t的可能性比较大,而量测来自目标t的可能性则较小。对于图2中的关联假设(1,1,1)和(2,2,2),传统CMS-MHT算法中航迹t的得分增量是相同的,这会导致航迹-量测关联假设的不确定性增大,进而产生错误关联现象。在密集杂波环境下,虚警量测落入航迹关联门的可能性大,传统航迹得分计算方法容易产生错误关联现象,导致跟踪性能下降。
针对传统CMS-MHT算法中存在的上述问题,在传感器测量误差较小的情况下,本文基于虚警与目标量测的空间分布特点,引入角度信息辅助的航迹得分计算。对于图2的两种关联假设(1,1,1)及(2,2,2),角度信息的引入可使航迹t的得分增量不同,对于更符合实际情况的关联假设(2,2,2)的得分增量,应大于更可能是错误关联的假设(1,1,1)的得分增量。
假设航迹t在k时刻预测位置为Z(k),对k时刻的关联假设与航迹t关联的量测均落入通过预测位置Z(k)定义的航迹关联门内。传统CMS-MHT算法是根据量测l≠0 i与预测位置Z(k)之间的距离计算航迹得分,没有充分利用传感器量测和虚警的空间分布特点。这里给出一种新的航迹得分计算方法。如果k时刻的关联假设为正确关联,则与航迹t关联的量测应该集中分布在目标实际位置附近。如图3所示,我们用向量和向量的夹角表示量测,与目标实际位置的角度差异。当传感器测量误差比较小时,如果关联假设为正确关联,则量测对应的角度θ应该都比较小。目标ti在k时刻的实际位置是未知的,对于关联假设,可以基于多个传感器对航迹t在k时刻的量测数据,得到其最大似然估计。
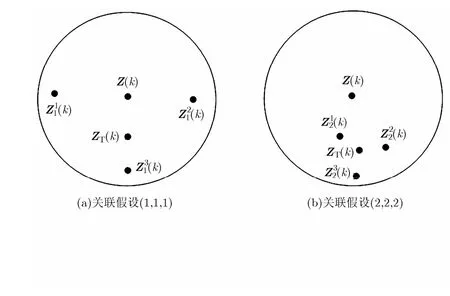
图2 航迹预测位置和传感器量测位置关系

图3 角度信息示意图
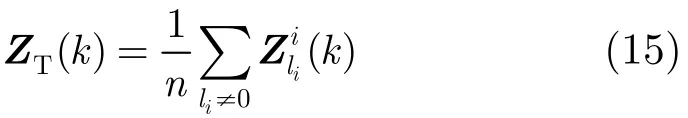
其中,n为关联假设(l1, l2,…,lNs)中与航迹关联的量测的数目。定义预测位置Z(k)和ZT(k)的一个加权位置为



Si(k )为k时刻传感器i对航迹t的量测预测协方差。从式(16)~式(18)可以看出,当传感器数目为1时,的定义与单传感器MHT算法中相同。当传感器数目大于1时,与传统CMS-MHT算法不同,同时体现了量测与航迹t预测位置Z(k)和实际位置ZT(k)的差异。
在本文CMS-MHT算法中,对于k时刻的关联假设(l1, l2,…,lNs),当li≠0时,即传感器i的量测来自目标t,定义航迹t在k时刻相对传感器i的得分增量为


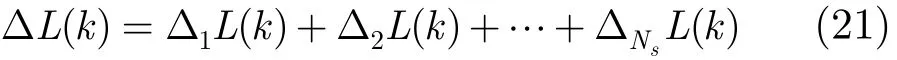
假设航迹t在k-1时刻得分为L( k-1),则对于k时刻关联假设(l1, l2,…,lNs),航迹t在k时刻的得分L( k)为
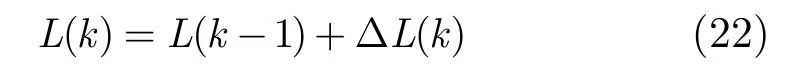
对于关联假设(l1, l2,…,lNs),航迹t在k时刻得分增量ΔL( k)的大小,反应了在k时刻和航迹t关联的所有量测均来自目标t的可能性大小,ΔL( k)值越大,说明可能性越大。对于相同类型的多传感器目标跟踪,当传感器测量误差比较小时,上述集中式多传感器目标跟踪方法可以降低数据关联的不确定性。
4 航迹树剪枝
由于MHT算法的高复杂性,可用的MHT实现里一定会应用若干降低复杂度的策略,在保持一定算法性能的同时减少对计算量和存储的需求。对CMS-MHT算法而言,由于多个传感器的量测集中处理,更加需要进行有效的假设管理。一个目标的所有时刻的量测-航迹关联假设组成了一个航迹树,而假设删减技术可以看成航迹树的剪枝。本文CMS-MHT算法在实现时所采用的航迹树剪枝技术有:基于得分的航迹删除和确认[15]、N回扫剪枝[16]、以及基于全局概率的航迹删除[17]。
当完成量测-航迹关联并计算角度信息辅助的航迹得分后,首先进行基于得分的航迹删除和确认。基于得分的航迹删除和确认方法使得得分大于阈值的航迹得到确认,删除得分小于阈值的航迹。N回扫剪枝是一种通过限制航迹树深度来控制航迹分枝数量的方法。在本文CMS-MHT算法中,每一时刻保留多个航迹分枝,该时刻的航迹分枝在经过N个时刻以后要被剪枝,只保留N个时刻后概率最大的全局假设中的航迹所在的分枝。在N回扫剪枝前,需要求解k最优全局假设。
为了降低计算复杂性,算法同时采用了分簇处理[17]。通过分簇能够将航迹集合划分成较小的子集,而全局假设产生这一组合问题可以在每个簇中独立地进行,从而减小了问题规模。对于全局假设的生成问题,k最优分配算法为最常用的方法[18]。在求解k最优全局假设的同时,航迹的全局概率也将给出。当完成N回扫剪枝后,进行基于全局概率的航迹删除,即删除全局概率低于阈值的航迹。
5 仿真验证
仿真场景为4个传感器对3个目标进行跟踪。各传感器在直角坐标系中的位置分别为S1(-20000 m, 55000m), S2(-160000 m,20000 m), S3(-100000 m, 20000 m), S4(40000 m,55000 m)。目标的状态向量由目标的x和y向位置、x和y向速度构成,3个目标的初始状态向量分别为T1(-20000 m,30000 m, -400 m/s,50 m/s),T2(-10000 m,40000 m, -400 m/s,-20 m/s),T3(-180000 m,30000 m, 250 m/s,100 m/s)。目标1作匀速直线运动,目标2在第50个跟踪时刻至第62个跟踪时刻发生机动,目标3在第62个跟踪时刻至第75个跟踪时刻发生机动。各个传感器的性能参数相同,扫描周期为4 s,探测概率为0.8, x和y向测量误差标准差均为100 m。仿真的跟踪步数为100,过程噪声标准差为10 m,杂波密度为1×10-8个/m2,新目标密度为1×10-13个 / m2。图4给出了3个目标的真实轨迹和传感器分布,“Δ”表示传感器所在位置。图5给出了一次仿真中传感器S2的量测分布。
一条航迹的寿命为其存在的扫描时刻数。对于跟踪算法所给出的一条航迹,在其存在的某一扫描时刻,如果与该航迹关联的所有量测均来自同一个真实目标,则称该航迹该时刻属于该真实目标。如果跟踪算法所给出的一条航迹属于同一个真实目标的时刻数与该航迹寿命的比值大于50%,则称该航迹为该真实目标的真航迹。
对于一个真实目标,如果在某一扫描时刻没有真航迹与其对应,则称该真实目标在该时刻的信息被漏掉。一个真实目标的漏情率为其信息被漏掉的扫描时刻数和总扫描时刻数的比值。在检测概率较低时,一条真实目标航迹可能由于漏检而被跟踪算法拆分为若干条较短的航迹,因此一个真实目标可能对应着多条真航迹,较长的真航迹寿命通常表示较好的航迹完整性。通过每个真实目标对应的最长真航迹寿命可以对航迹完整性进行评估。
针对上述给定的传感器测量误差,表1给出了所有真实目标的漏情率,表2给出了所有真实目标的最长真航迹寿命,蒙特卡洛仿真次数为50。图6为传统CMS-MHT算法一次仿真跟踪结果,图7为本文算法一次仿真跟踪结果。从表1可以看出,本文算法对所有真实目标的漏情率均不同程度地低于传统CMS-MHT算法的漏情率,也就是说本文算法漏掉真实目标信息的可能性比较小。从表2可以看出,本文算法得到的每个真实目标的最长真航迹寿命均不同程度地大于传统CMS-MHT算法,即得到的航迹完整性较好。从图6和图7也可以看出本文算法跟踪结果好于传统CMS-MHT算法。
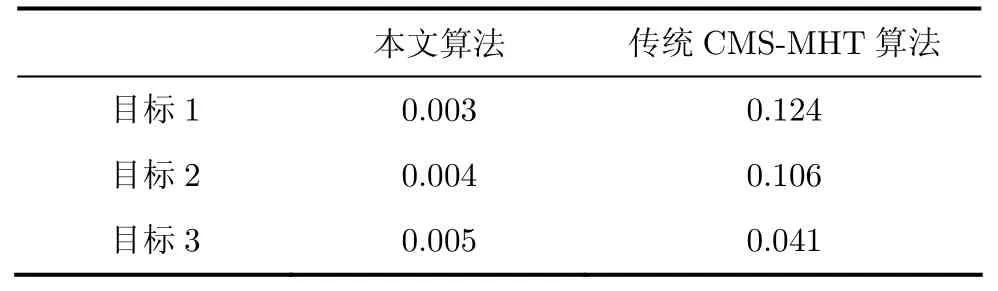
表1 漏情率
为了说明传感器测量误差对本文算法性能的影响,当传感器x和y向测量误差标准差均从60 m到240 m变化时,图8给出了目标1的最长真航迹寿命的变化曲线。从图8可以看出,当传感器测量误差标准差在200 m以内时,本文算法得到的目标1的最长真航迹寿命相对传统CMS-MHT算法优势比较大,也就是说本文算法得到的航迹完整性好于传统CMS-MHT算法。当传感器测量误差标准差大于200 m时,本文算法得到的目标1的最长真航迹寿命相对传统CMS-MHT算法的优势变小。随着传感器测量误差的变大,本文算法相对传统CMS-MHT算法的优势总体处于下降趋势。

图4 目标真实轨迹和雷达分布

图5 传感器S2的量测分布

图6 传统CMS-MHT算法一次仿真跟踪结果
上述实验结果表明,在一定的传感器测量误差范围内,与传统CMS-MHT算法相比,本文算法可以有效降低目标的漏情率,同时有着更好的航迹完整性。
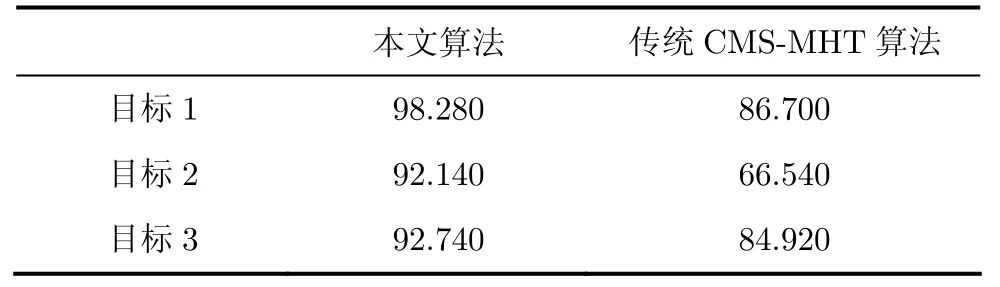
表2 最长真航迹寿命(单位:跟踪步数)
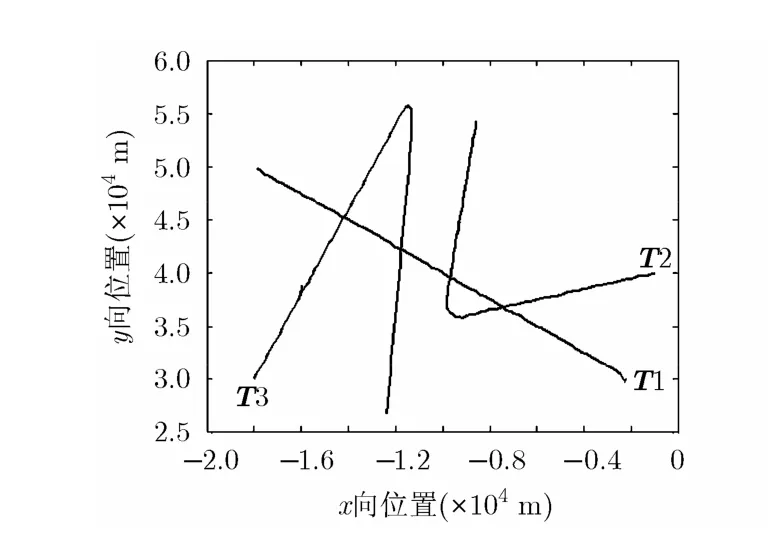
图7 本文算法一次仿真跟踪结果
6 结束语
本文针对密集杂波环境的多传感器多目标跟踪问题,提出了一种角度信息辅助的CMS-MHT算法。基于虚警与目标量测的空间分布特点设计了新的角度信息辅助的航迹得分计算方法,在传感器测量误差较小时,可以得出更符合实际情况的航迹分值,进而降低了航迹-量测关联假设不确定性,提高了航迹的质量。仿真结果表明,在密集杂波环境下,新的算法可以获得比传统CMS-MHT算法更好的跟踪效果,即显著地降低了漏情率,同时延长了最长真航迹寿命。

图8 目标1的最长真航迹寿命变化曲线
[1] Ling Qing, Fu Yin-fei, and Tian Zhi. Localized sensor management for multi-target tracking in wireless sensor networks[J]. Information Fusion, 2011, 12(3): 194-201.
[2] Liu Han and Zhang Lei. Clustering methods for multi-sensor data fusion[C]. Proceedings of the 2012 International Conference on Industrial Control and Electronics Engineering, Xi’an, China, 2012: 1166-1169.
[3] Gao Xin-bo, Chen Jin-guang, Tao Da-cheng, et al.. Multi-sensor centralized fusion without measurement noise covariance by variational Bayesian approximation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 718-727.
[4] 韩崇昭, 朱洪艳, 段战胜. 多源信息融合[M]. 第2版, 北京:清华大学出版社, 2010: 250-260.
[5] Nam T P, Karianto L, and Wong M. Combining JPDA and particle filter for visual tracking[C]. Proceedings of the IEEE International Conference on Multimedia and Expo, Suntec City, Singapore, 2010: 1044-1049.
[6] Huang Xiao-peng, Zeng Dong, and Peng Dong-liang. A method of multi-sensor and multi-target Tracking and fusion based on double-threshold technique[J]. International Journal of Sensors Wireless Communications and Control, 2012, 2(1): 61-66.
[7] Chris K and Ben S. Multitarget detection and tracking using multisensor passive acoustic data[J]. IEEE Journal of Oceanic Engineering, 2011, 36(2): 205-218.
[8] Lennart S, Daniel S, and Marco G. Set JPDA filter for multitarget tracking[J]. IEEE Transactions on Signal Processing, 2011, 59(10): 4677-4691.
[9] Stefano C and Craig C. A hierarchical MHT approach to ESM-Radar fusion[C]. Proceedings of the 15th International Conference on Information Fusion, Singapore City, Singapore, 2012: 677-683.
[10] Stefano C and Craig C. Addressing the greedy-target problem in multiple hypothesis tracking[C]. Proceedings of the IEEE Aerospace Conference, Big Sky, USA, 2011: 1-10. [11] Blackman S S and Popoli R. Design and Analysis of Modern Tracking Systems[M]. The First Edition, Norwood, MA: Artech House, 1999: 360-369.
[12] Pollard E, Benjamin P, and Michele R. Hybird algorithms for multi-target tracking using MHT and GM-CPHD[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 832-847.
[13] Hernandez M, Benavoli A, and Farina A. Performance measures and MHT for tracking move-stop-move targets with MTI sensors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 996-1025.
[14] Li Sheng-wei, Feng Xiao-liang, and Lu Ya-zhou. A measurements fusion filter for the multi-sensor system with correlated noises[C]. Proceedings of the 10th World Congress on Intelligent Control and Automation, Beijing, China, 2012: 4458-4462.
[15] Ren Xiao-yi, Huang Zhi-pei, Liu Dong-yan, et al.. Multiple object video tracking using GRASP-MHT[C]. Proceedings of the 15th International Conference on Information Fusion, Singapore City, Singapore, 2012: 330-337.
[16] Jamie S, Branko R, and Dmitri K. A pedestrian multiple hypothesis tracker fusing head and body detections[C]. Proceedings of the International Conference on Digital Image Computing: Techniques and applications, Hobart, Australia, 2013: 1-8.
[17] Blackman S S, Dempster R J, and Reed R W. Demonstration of multiple hypothesis tracking (MHT) practical real-time implementation feasibility[C]. Proc. SPIE 4473, Signal and Data Processing of Small Targets 2001, San Diego, CA, USA, 2001: 470-475.
[18] Yu Juan, Wang Jun, Wei Shao-ming, et al.. Multi-hypotheses based data association for scatter centers of spin cone-shape target[C]. Proceedings of the 2012 IEEE 11th International Conference on Signal Processing, Beijing, China, 2012: 1957-1962.
王 欢: 女,1988年生,博士生,研究方向为雷达信号处理.
孙进平: 男,1975年生,教授,研究方向为高分辨率雷达信号处理、通信及图像中的模式识别、压缩感知、稀疏微波成像等方面的研究.
付锦斌: 男,1991年生,博士生,研究方向为雷达信号处理.
Angle Aided Centralized Multi-sensor Multiple Hypothesis Tracking Method
Wang Huan Sun Jin-ping Fu Jin-bin Mao Shi-yi
(School of Electronic and Information Engineering, Beihang University, Beijing 100191, China)
For multi-target tracking in heavily cluttered environment, the number of measurement-to-track association hypotheses in each scan grows rapidly in traditional Centralized Multi-Sensor Multiple Hypothesis Tracking (CMS-MHT) method, which leads that the uncertainty of data association greatly increases such that correct association can hardly be given using traditional track score resulting in high leakage rate and effects of track splitting. Based on the space distribution characteristics of false alarm and target measurement when the sensor measurement error is small, for target tracking using multiple sensors of same type this paper proposes a new angle aided CMS-MHT method, which designs angle aided track score computation to reduce the uncertainty of measurement-to-track association. In such a way, the proposed angle aided CMS-MHT can provide better association hypotheses compared with traditional CMS-MHT. The experimental results illustrate that angle aided CMS-MHT reduces leakage rate and has better track integrity in heavily cluttered environment.
Multi-Target Tracking (MTT); Multiple Hypothesis Tracking (MHT); Multi-sensor; Centralized; Angle information
TN953
A
1009-5896(2015)01-0056-07
10.11999/JEIT140230
2014-02-24收到,2014-07-03收到
国家973计划项目(2010CB731903)资助课题
*通信作者:王欢 xisubu@126.com

