时间域电磁勘探数据的模拟退火法反演研究

张建国 武 欣 赵海涛② 齐有政② 方广有

1 引言

电磁勘探方法对高阻性异常体有较强的探测能力，已成为油气资源勘探的一种有效方法[1,2]。利用接地长导线向地下发送电磁场（一次场），地下异常体中激励的感应涡流将产生感应电磁场（二次场），利用接收机观测感应电磁场，再通过数据解释来推断地下电性结构的空间分布，进而确定地下异常体的位置和规模。时间域电磁法（Time-domain ElectroMagnetic, TEM）在一次场的关断间歇来观测二次场，得到的观测数据是没有一次场“污染”的电磁响应，通过数据解释可获得更真实的地电模型参数[3,4]。

目前，电磁勘探中地电模型的精确反演是一大难题。虽然一些学者开展了电磁法的多维反演理论研究，但需要指出的是，这些方法应用于实践还存在许多问题，能有效应用到工程中的仍然只是1维反演[5,6]。其中1维线性化反演方法仍然是电磁勘探中普遍采用的反演方法[7,8]。然而，由于其反演过程是采用梯度搜索方法对非线性模型进行线性化近似，这必然从理论上带来了误差；同时，由于地电模型的非惟一性，此类方法容易收敛于局部极小值，并高度依赖于初始模型的选择，其数据解释结果容易偏离真实的大地模型。

因此，本文开展 TEM 数据的非线性反演方法研究，将模拟退火（Simulated Annealing, SA）算法应用于TEM数据最优解的搜索[911]-。虽然SA算法已开始在地震勘探中应用，但是由于 TEM 地电模型的高度非线性和非惟一性，其在 TEM 数据反演中的应用鲜有文献讨论。本文首先采用双重数字滤波方法提高TEM正演计算的速度，缩短SA算法反演的迭代时间。同时，改善 SA算法的搜索控制策略，使算法在全局最优解的搜索过程中能自适应地调节搜索步长，并逐步缩小搜索范围，提高算法的搜索效率。与Marquardt反演方法（线性化反演方法）进行对比实验，结果表明 SA算法能在不依赖于初始模型和梯度的条件下，有效地摆脱局部最优，搜索到全局最优解。

2 基于双重数字滤波的TEM正演计算

如图1所示，TEM方法通过接地电极AB向地下发射双极性方波形式的激励信号，双极性方波的每个下降沿可视为地电模型的阶跃激励信号，同时利用多通道接收机采集具有地下异常信息的电磁响应数据。其中，ρn和hn分别为第n层介质的电阻率和厚度（n = 1 ,2,… , N ）, T和τ分别为双极性方波的周期长度和占空比，角度Φ为发射点与接收点连线与x轴的夹角。

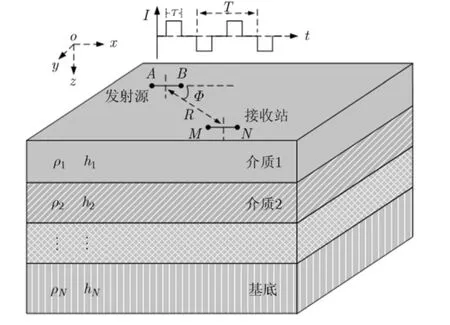
图1 地电模型和TEM方法示意图

地电模型的频率域电磁场满足的赫姆霍兹（Helmholtz）方程为

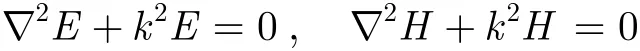
其中，k为波数。由于TEM方法是对时间域的阶跃场进行观测，因此正演的思路为：首先求解频率域的谐变场，然后根据阶跃场和谐变场的关系，得到频率域的阶跃场 G （ ω） = F （ ω）/（i ω） ，最后利用傅里叶逆变换或者拉普拉斯逆变换，获得G（ω）对应的时间域的阶跃场g（ t） 。

对于均匀各向同性的层状大地模型，电偶极源激励的谐变场（正演中只考虑水平电场 Ex和垂直磁场 Hz）的表达式为

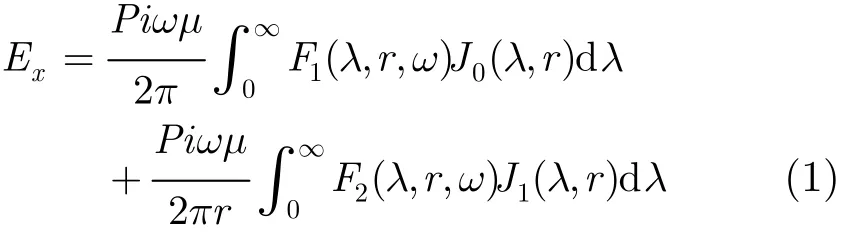
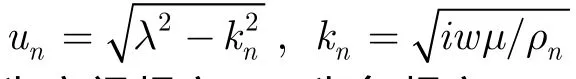
根据阶跃场和谐变场的关系，得到频率域的阶跃场的表达式为

对式（3）和式（4）获得的频率域电磁响应，通过拉普拉斯逆变换可获得时间域电磁场的表达式。显然，这类方法计算量太大，采用 Gaver-Stehfest算法可以快速实现频率域电磁场向时间域电磁场的转换[12]：

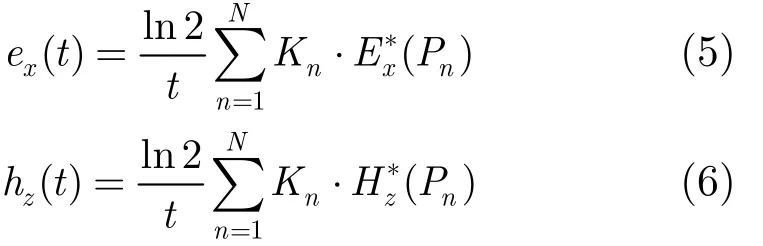
其中，Kn为预先确定的Gaver-Stehfest算法的数字滤波系数，Pn= n ⋅ ln 2 /t 。ex（ t）,hz（ t） 为频率域阶跃场对应的时间域表达式，是TEM方法的正演结果。

对于式（3）和式（4）中 Bessel函数非线性积分的计算，使用快速Hankel变换方法可以获得令人满意的数值精度。将积分中Bessel函数的两个变量（λ,r）通过指数代换，进而把非线性积分计算转换成卷积形式。然后将卷积离散化，通过预先确定的数字滤波系数，获得高精度的数值解[13,14]。

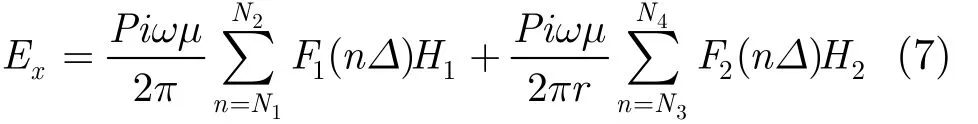
其中 H1,H2和 H3分别为预先确定的快速Hankel变换的数字滤波系数，Δ为滤波系数的坐标间隔。滤波系数越长，数值解的精度越高。

比较式（7）和式（8）可知，与 Hz相比， Ex包含的地下信息更为丰富。但是，由于反演解释的复杂性不同，TEM 方法通常采用 Hz作为观测数据。本文采用双重数字滤波的正演方法，能有效地简化正演计算过程，实现电磁场的快速、精确计算，本文反演计算针对 Ex场进行。在搭载 Intel Core i3-2120 CPU（主频3.3 GHz），内存2 GB的PC机上，针对3层地电模型，20个时间点的正演计算耗时仅0.056 s。

3 模拟退火法反演步骤

层状地电模型的参数包括每层的电阻率ρn和厚度 hn，把这些参数看作一个数组向量，则地电模型可记为x。由于地电模型是高度非线性的，所以通过电磁场的观测值进行反演，推导地电模型的参数的过程属于非线性最优化问题。将其转化为一个迭代求解过程，且每次迭代过程中都通过一定的方法控制变量的变化，使目标函数S（x）随着迭代的进行而逐步下降，从而达到逼近最优解的目的。地电模型的最优解 xopt应满足： S （xopt）= min（S （x ） ） ，即

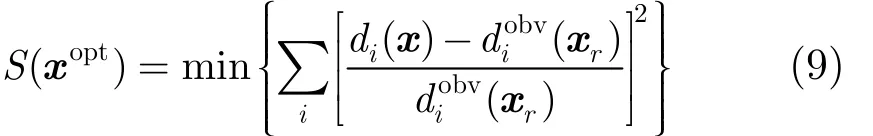
式中rx为真实模型，obv（）dx为观测数据，（）d x表示根据真实模型进行正演计算得到的电磁场理论数据。

模拟退火（SA）算法应用于求解多元函数全局最小值，不依赖于初始模型的选择，并能有效地摆脱局部最小值，同时不需要计算复杂的雅克比矩阵[15,16]。在地震勘探领域中，SA算法作为一种全局优化算法，得到越来越多的应用。但是，由于地电模型的高度非线性和非惟一性，采用 SA算法的TEM数据的反演，鲜有研究文章发表。本文基于双重数字滤波方法的正演计算，通过改进的SA算法，实现了TEM方法的准确、快速反演。

当 SA算法的目标函数值较大时，温度取较大值，那么模型迭代的步长可以取较大值；反之亦然。因此，反演不会陷入局部极小值，保证了反演过程的全局最优化。SA算法通过温度来控制迭代过程，使用收敛阈值来判断迭代结果是否被接受。SA算法的流程图如图2所示，其中：n为内部循环迭代次数，m为外部循环迭代次数，mT 为温度，η为每次迭代中产生的一个随机数。当目标函数（）S x小于收敛阈值或者m大于最大循环次数时，迭代过程结束。使（）S x小于收敛阈值的地电参数，即为SA算法的反演结果。

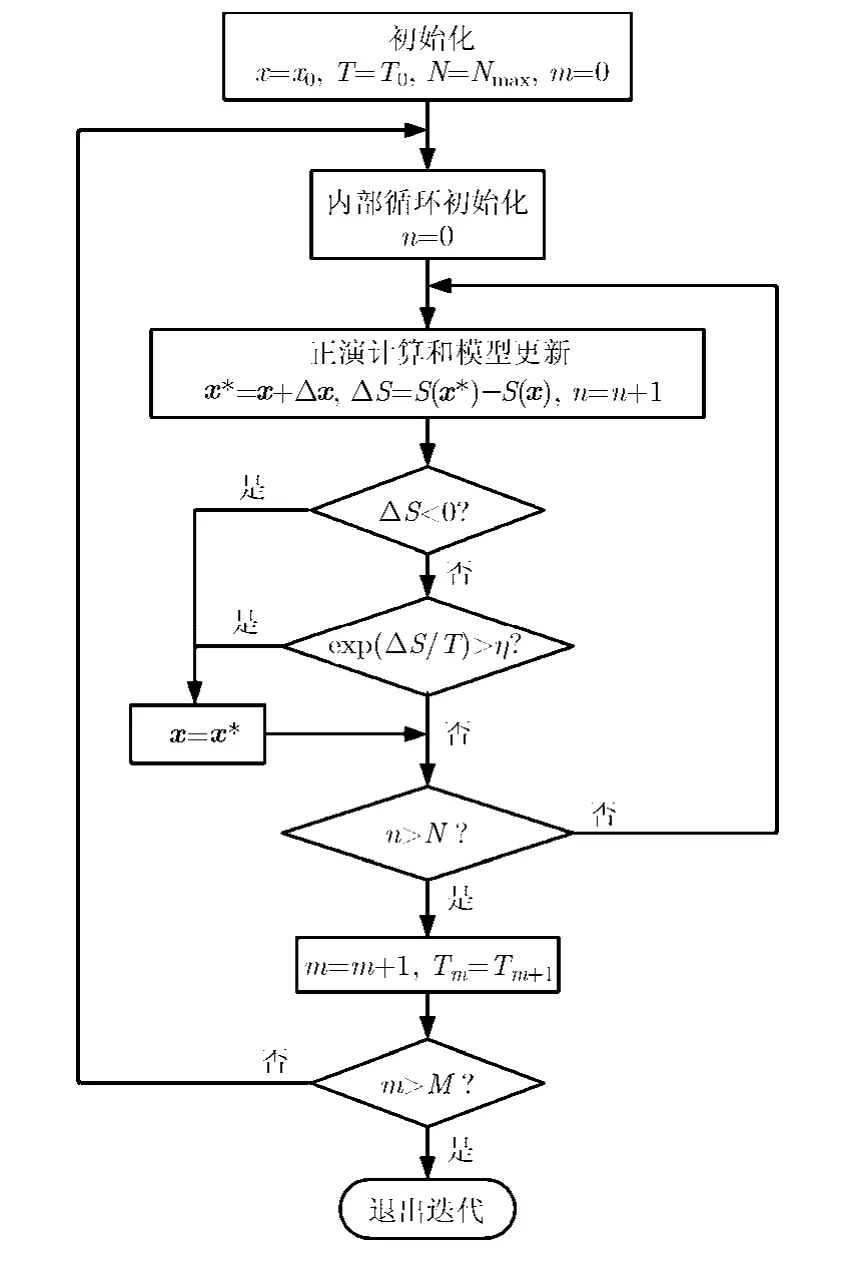
图2 模拟退火算法的流程框图

4 仿真与分析

4.1 SA算法的改进

传统的 SA算法采用随机扰动的搜索策略，效率较低，不能满足 TEM 方法大数据量、高复杂度的非线性反演的需求。本文联合柯西概率分布与“扰动因子”，来设定地电模型的步长：

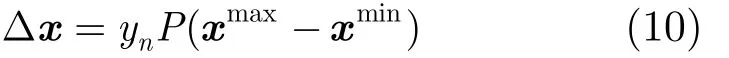
其中，y= s ign（η - 0 .5）T [ （1 + 1 / T ）2ηn-1-1]为基

nnnn于柯西概率分布的修正参数，扰动因子为 P =exp（5.0 ⋅Nna/Ns），式中ηn为（0,1）之间的随机数，Tn为温度控制变量， Ns为内部循环的总次数， Nna为每个内部循环中步长未被接受的次数，系数 5.0是经验参数。

此优化策略具有以下特点：（1）ny根据温度来调节每次迭代的步长，高温时进行大范围的搜索，低温时减小搜索范围，仅在当前反演模型附近进行搜索，ny能根据nT 实现高效率的全局搜索；（2）P能根据步长被拒绝的次数而动态变化，当次数增大时，说明当前模型远离真实值，要加大扰动值P，进而扩大搜索范围。每次内部循环结束后，naN 被置零，SA算法重新进行全局搜索。

4.2 3层模型的仿真结果与对比分析

针对油气资源勘探，设置一个含有高阻油气层的1维层状大地模型，以验证本文反演方法的有效性。地电模型共含有3层水平各向同性介质，表层介质的电阻率 ρ1= 5 0.0 Ω ⋅m ，厚度 h1= 2 00.0 m；中间层介质表征油气层的电学特性，设置其电阻率为 ρ2= 1 000.0 Ω ⋅m ，厚度 h2= 5 0.0 m；底层为均匀半空间，介质的电阻率 ρ3= 1 00.0 Ω ⋅m ，这是TEM方法典型的地电模型。采用 Ex作为观测数据，Ex比其它场分量含有更多的地下异常信息。发射电流I= 100A，双极性方波的频率 f = 1 Hz（占空比τ为 0.25），发射线长度AB = 2 00m，接收线长度MN = 1 00 m，偏移距 r = 2 km。为了检验TEM方法对高阻异常体的探测能力，针对以上模型，采用基于双重数字滤波的正演方法，在有、无异常条件下分别进行计算，得到的观测数据如图3所示。由图3可知，两条曲线在0.1～10 ms时间段内的差异非常明显，证明了 TEM 方法对高阻异常体有较强的探测能力。

将上述含有高阻异常体的正演仿真结果（0.1～10 ms时间段）作为反演对象，分别使用改进的 SA方法和传统线性化反演方法的代表Marquardt方法，对大地模型的参数（ρ1, ρ2, ρ3,h1和 h2）进行反演，确定地电模型的参数值，并对比二者结果。基于上述模型参数和正演仿真数据，先使用Marquardt方法进行1维反演。设定地电模型的初始值为 x0=（80, 300, 800, 100, 150），进行10次反演计算，取10次结果的平均值作为地电模型的参数估计值。目标函数随着迭代次数的增加而逐渐减小，收敛曲线如图4所示，目标函数最终收敛于 2 × 1 0-4，得到的反演结果平均值如表1（电阻率单位为Ω⋅m，厚度单位为m）所示。由表1结果可知，Marquardt方法的反演结果最终陷于局部最小值，没有获得全局最优解，偏离真实模型参数。

采用相同的模型参数和正演仿真数据，再采用SA算法进行反演计算。仍然设定地电模型的初始值为 x0=（80, 300, 800, 100, 150），模型空间为真实值的±40%，内部循环次数N= 2 00，外部循环最大次数 M = 5 00。根据反演的经验，外部循环的温度控制变量的初始值设定为 T0= 1 0，并按照 Tm=T0⋅0. 9 7m的指数形式变化；温度控制变量的设置要多次尝试，以适应模型的扰动和目标函数的递减趋势。仍然进行10次反演计算，取结果的平均值。

目标函数S（x）的收敛阀值设为S= 1 0-6，即当0S（x）＜S0时，SA算法停止搜索，认为当前的模型是满足反演收敛条件的真实模型。图5为目标函数收敛曲线，相应的反演结果平均值如表1所示。需要指出的是，基于梯度的反演方法的目标函数随着迭代次数的增加而逐渐减小（图4），SA算法的目标函数是波动式的逐步减小（图5），正是由于波动式的收敛曲线使得SA算法能跳出局部极小值。将SA算法的反演结果代入正演计算中，并与真实模型参数的正演计算结果对比（如图 6所示），二者曲线基本一致，证实了反演结果的有效性。

表1 3层模型的反演结果对比

图3 含有异常和没有异常的阶跃响应对比图

图4 3层模型Marquardt方法的收敛曲线

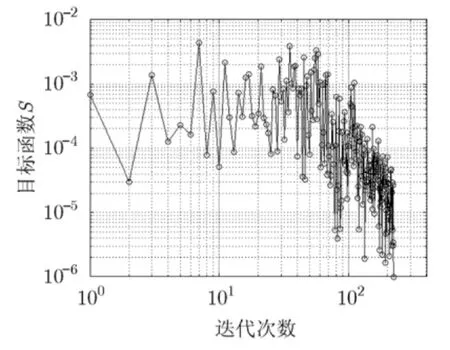
图5 3层模型SA方法的收敛曲线

在搜索过程中，SA算法通过改进的搜索策略能成功跳出局部极小值。在跳出局部极小值的过程中，目标函数是增大的；但随着迭代的进行，搜索会逐步向全局极小值靠近，目标函数也随之逐步减小，最终在全局极小值处收敛。为了验证算法的有效性，还对反演数据加入了5%的随机噪声，进行10次反演计算，同样取平均值得到反演结果如表1所示。

以下是对反演结果的分析：

（1）SA算法有效实现了对TEM方法中xE 仿真数据的反演，得到的模型参数与真实值基本一致。通过与Marquardt方法反演结果的对比，进一步证实了SA算法搜索全局最优解的能力。

（2）表1的反演结果表明，参数2ρ与其它参数相比，误差率较大。这是因为在xE场值的正演计算中，参数2ρ对场值的贡献较小，相关性较弱，所以xE的观测数据对其不够敏感，误差相对较大。

（3）加入噪声后，反演误差增大，但是反演误差小于5%，仍然在可接受的范围内，通过多次反演取平均值的方法，提高了计算结果的精度。

4.3 5层模型的仿真结果与对比分析

对于 TEM 数据的反演方法验证，一般只采用典型的3层地电模型。为了进一步测试本文改进的SA算法对TEM数据反演的有效性，将3层模型扩展至5层模型，在高阻油气层的上方和下方各加 1层电阻率为300 Ω⋅m的介质，地电模型的初始值为x0=（70, 150, 200, 600, 700, 70, 200, 700, 150），仍然采用3层模型中的收发参数。

采用Marquardt方法对上述模型的正演数据进行反演操作，同样取10次反演结果的平均值作为地电模型参数的估计值。目标函数的收敛曲线如图 7所示，Marquardt方法在迭代21次后，目标函数最终收敛于 1 .6 × 1 0-4，得到的反演结果平均值如表2（电阻率单位为Ω⋅m，厚度单位为m）所示。与3层模型的反演结果相比，5层模型的反演结果误差更大，Marquardt方法的搜索过程陷于局部最小值，反演结果偏离全局最优解。

采用SA算法对相同的正演数据进行反演操作，地电模型的初始值也与Marquardt方法相同，模型空间为真实值的±40%，内部循环次数N= 2 00，外部循环最大次数 M = 1 000。温度变量的初始值设置为 T0= 1 0，并按照 Tm= T0⋅0. 9 7m的指数形式变化。仍然进行10次反演计算，取结果的平均值。目标函数S（x）的收敛阈值仍然为S= 1 0-6，图8为目标函0数收敛曲线，相应的反演结果平均值如表2所示。SA算法的目标函数仍然波动式减小，在迭代过程中避开多个局部极小值，进而逼近全局最优，获得比较真实的地电模型估计值。SA算法在外部循环迭代474次时，获得低于收敛阀值的目标函数值，此时的反演结果是TEM数据对应的全局最优解。

以下是对反演结果的分析：

（1）SA算法基本实现了5层模型TEM数据的反演，获得的模型参数估计值能反映真实模型的特性，模型中介质电阻率由上而下为“低-高-低”的变化趋势，在反演结果中得到了反映；与Marquardt方法相比，SA方法对TEM数据反演更准确、更有效。

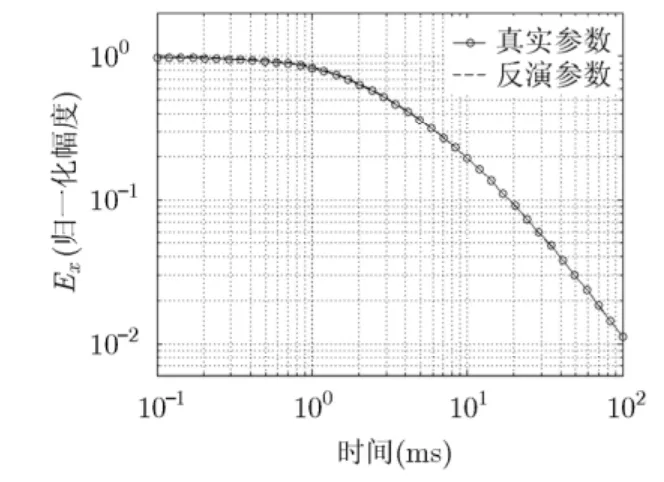
图6 SA算法反演参数与真实参数的正演计算对比

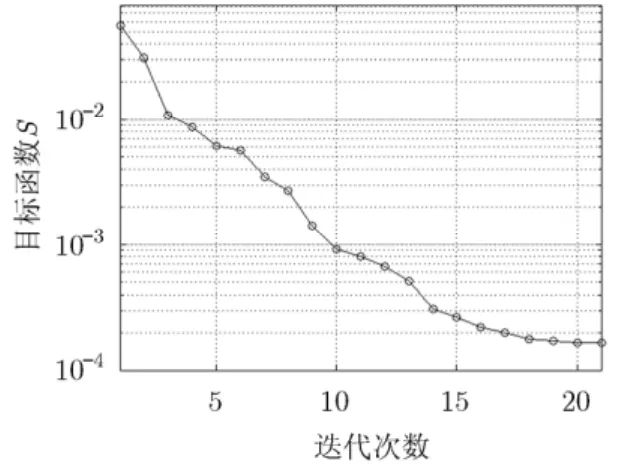
图7 5层模型Marquardt方法的收敛曲线

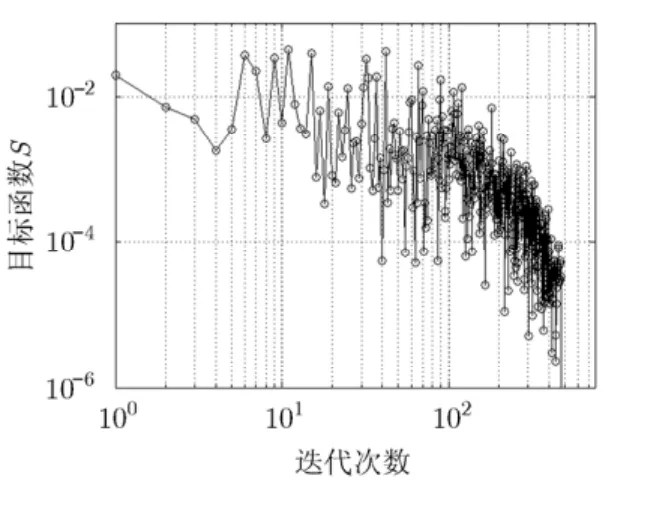
图8 5层模型SA算法的收敛曲线

表2 5层模型的反演结果对比

（2）由于5层模型的参数较多，相应的反演难度较大，因此，反演结果的误差增大；但是，SA方法仍然能有效获得模型的关键信息，如第3层（高阻油气层）和第1层（表层）的电阻率及其厚度信息。

（3）随着模型参数的增多，反演难度加大，在加入5%噪声条件下，反演结果与真实值有一定偏差，SA方法对噪声的抑制能力降低。

5 结论

本文提出了基于双重数字滤波的正演方法，实现了快速、精确的正演计算。将SA算法应用于TEM方法的反演中，修改了算法的搜索策略，与传统反演方法的对比实验验证了 SA算法的有效性。主要结论如下：（1）对于地下高阻性异常，xE 比其它场分量含有更丰富的地电信息，但其数据解释难度较大。本文基于双重数字滤波方法的正演计算，简化了计算过程，可快速获得较高精度的电磁响应，给xE场的数据反演提供了理论支撑。（2）SA 算法的搜索策略可以有效地实现层状大地模型的反演，在搜索全局最优解的过程中，目标函数不是依次减小，而是波动式减小，算法可以跳出局部极小值，实现全局优化。（3）在正演计算过程中，参数对电磁场的贡献越大，其反演的精度越高；加入随机噪声后，SA算法的目标函数依然能收敛，表明 SA算法有一定的抗干扰能力。（4）随着模型层数的增加，反演难度加大，但是，对于TEM方法常用的3层及其5层模型，SA算法都能获得比较真实的地电模型参数。由于 SA算法进行随机搜索和步长的动态调整，以避开局部极小值，SA算法需要的迭代次数较大，相应的反演耗时较长，反演计算时间在数个小时之内；但是，这仍然满足TEM方法的要求。

[1] Zhang Jian-guo, Wu Xin, Qi You-zheng, et al.. Research on 3D marine electromagnetic interferometry with synthetic sources for suppressing the airwave interference[J]. Applied Geophysics, 2013, 10（4）: 373-383.

[2] 何继善. 海洋电磁法原理[M]. 北京: 高等教育出版社, 2012:3-4 .

[3] 张建国, 武欣, 齐有政, 等. 时间域编码电磁勘探方法研究[J].雷达学报, 2014, 3（2）: 158-165.Zhang Jian-guo, Wu Xin, Qi You-zheng, et al.. Investigation on time domain coded electromagnetic exploration method[J].Journal of Radars, 2014, 3（2）: 158-165.

[4] Ziolkowski A, Hobbs B A, and Wright D. Multitransient electromagnetic demonstration survey in France[J].Geophysics, 2007, 72（4）: F197-F209.

[5] 刘颖, 李予国, 柳建新, 等. 海洋可控源电磁场的一维反演[J].中国有色金属学报, 2013, 23（9）: 2551-2556.Liu Ying, Li Yu-guo, Liu Jian-xin, et al.. One-dimentional inversion of marine controlled-source electromagnetic fields[J].The Chinese Journal of Nonferrous Metals, 2013, 23（9）:2551-2556.

[6] 汤井田, 任政勇, 化希瑞. 地球物理学中的电磁场正演与反演[J]. 地球物理学进展, 2007, 22（4）: 1181-1194.

[7] 毛立峰, 王绪本, 陈斌. 直升机航空瞬变电磁自适应正则化一维反演方法研究[J]. 地球物理学进展, 2011, 26（1）: 300-305.

[8] 向阳, 于鹏, 陈晓, 等. 大地电磁反演中改进的自适应正则化因子选取[J]. 同济大学学报（自然科学版）, 2013, 41（9）:1429-1434.Xiang Yang, Yu Peng, Chen Xiao, et al.. An improved adaptive regularized parameter selection in magnetotelluric inversion[J]. Journal of Tongji University（Natural Science）,2013, 41（9）: 1429-1434.

[9] 孙娟娟, 黄宗潘, 杨大成. 基于模拟退火的移动业务分布预测算法[J]. 电子与信息学报, 2008, 30（9）: 2225-2228.

[10] 葛建军, 张春城. 基于模拟退火算法的机载脉冲多普勒雷达中重复频率选择研究[J]. 电子与信息学报, 2008, 30（3）:573-575.

[11] 张宇, 张晓娟, 方广有. 大尺度分层介质电特性参数的反演方法研究[J]. 物理学报, 2013, 62（4）: 044204.Zhang Yu, Zhang Xiao-juan, and Fang Guang-you. A data inversion method for electromagnetic scattering from large-scale layered medium[J]. Acta Physica Sinica, 2013,62（4）: 044204.

[12] Antonijevic S and Poljak D. A novel time-domain reflection coefficient function: TM case[J]. IEEE Transactions on Electromagnetic Compatibility, 2013, 55（6）: 1147-1153.

[13] Ding Ping-ping, Qiu Cheng-wei, Zouhdi S, et al.. Rigorous derivation and fast solution of spatial-domain green’s functions for uniaxial anisotropic multilayers using modified fast hankel transform method[J]. IEEE Transactions on Microwave Theory and Techniques, 2012, 60（2）: 205-217.

[14] Kong Fan-nian. Hankel transform filters for dipole antenna radiation in a conductive medium[J]. Geophysical Prospecting,2007, 55（1）: 83-89.

[15] Freethy S J, Shevchenko V F, and Vann R G L. Optimization of wide field interferometric arrays via simulated annealing of a beam efficiency function[J]. IEEE Transactions on Antennas and Propagation, 2012, 60（11）: 5442-5446.

[16] Wang Ruo, Yin Chang-chun, Wang Miao-yue, et al..Simulated annealing for controlled-source audio-frequency magnetotelluric data inversion[J]. Geophysics, 2013, 77（2）:E127-E133.