基于类DNA编码分组与替换的加密方案
张 顺 高铁杠
1 引言
在大规模网络化和数字化的今天,尤其是随着大数据和云计算的快速发展,保障数字信息在互联网上的安全可靠传输尤为重要。加密是一种常规且有效的解决方案。基于文献[1]提出的置乱(confusion)和分散(diffusion)理论,大量的加密方案被提出。传统的图像加密方案把像素作为基本单位,通过对像素值的置乱与替换实现加密操作。混沌系统具有良好的随机性,且对初值和参量非常敏感,因而被广泛应用与加密方案的设计[27]-。它们通常被用于置乱规则或者置乱矩阵的构造[2],或者被用于产生随机序列来与图像像素进行按位异或操作[2,3]。从二进制位面的层次来设计加密方案会更加有效。近年来,一些基于位面的加密方案被提出[810]-。文献[9]分析图像像素的各个位面的权重,对位面之间的关系以及性质等做了详细讨论,通过将图像像素位面分解重构并置乱来实现图像加密。文献[10]仅通过在位面层次的置乱就较好地实现了图像加密。不同于像素层次的置乱,位面层次的置乱不仅仅在视觉上,而且对一些统计信息比如直方图也实现了加密。
利用生物学编码和运算方案对图像进行处理和加密是最近几年新提出的思路。文献[3]首先将图像编码成 DNA序列;然后根据 DNA互补规则对该DNA序列进行随机次数的互补替换;最后将序列重新编码成图像,并通过按位异或混沌随机序列来实现图像加密。文献[4]对编码成DNA序列的3个通道做加法之后,分别用超混沌系统对3个通道进行置乱加密,然后再做混沌与序列的加法,最后解码生成加密后图像。从本质上讲,这些基于生物学编码的方案属于位面层次的加密方案,因此都取得了较好效果,但是它们大都仅仅利用了编码的形式。
基于生物学中 DNA编码和中心法则的思想,本文提出一种基于位面层次的编码分组加密方案。方案首先将图像编码成 DNA序列,之后编码成密码子(codon)序列,然后通过设计一种随机分组替换方案来实现图像的加密。主要的创新工作为:根据分子生物学的思想对图像进行位面层次的编码;通过密码子置乱和随机分组方案并结合编码后的序列实现了一种任意进制数制编码方案;由超混沌系统结合前面形成的任意进制数制编码方案产生加密控制信息;根据加密控制信息完成编码成密码子序列的图像的位面层次的替换操作,并最终实现图像的加密。从某种程度上讲,该方案实现了置乱与替换的融合。而且,相比于传统基于像素的置乱方案和近几年提出的基于位面的置乱方案,所提出的方案具有更大的密钥空间,更好的直观加密效果,而且,在加密安全性和加密效率上,也有明显的优势。
2 基础理论
2.1 DNA编码以及中心法则
DNA序列由4种核苷酸(分别为A, T, C, G)组成,如果用二进制编码表示,需要用两位二进制数据。常用的二进制DNA编码序列满足DNA互补规则,主要有8种对应方式,如表 1所示。

表1 DNA编码方式


集合中密码子的数目 S = 6 4,随机分组数组Y=[4,4,4,5,3,6,5,6,5,2,2,2,2,2,2,2,2,2,2,2],随机分组数目N= 2 0,随机分组名称分别为{A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T}。实际上表 2和表 3在结构上非常相似,它们都将64个密码子映射到20个分组当中。每次的密码子置乱和随机方案不同,生成的密码子分组表也不同。
2.2 混沌随机序列的产生

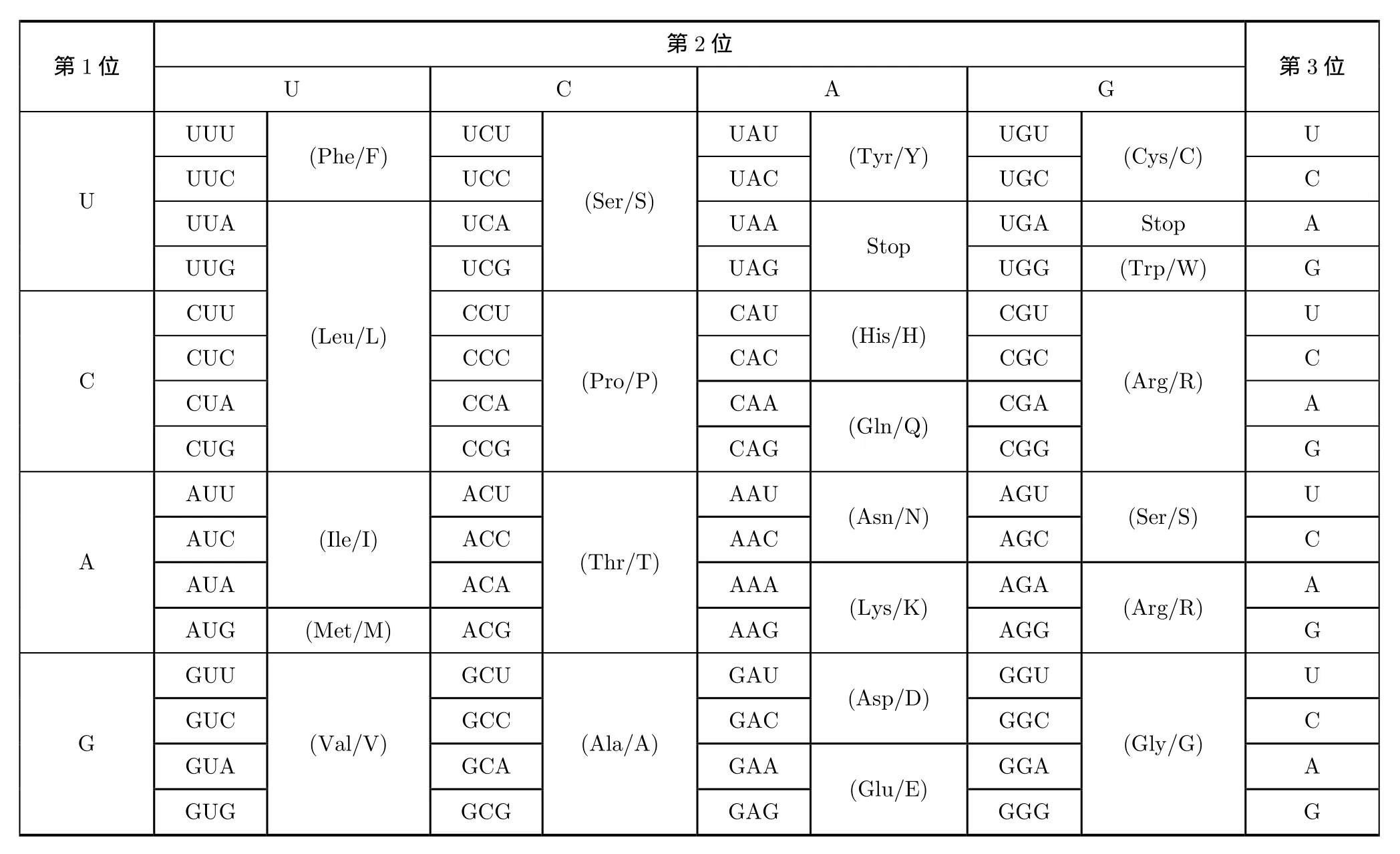
表2 标准密码子表
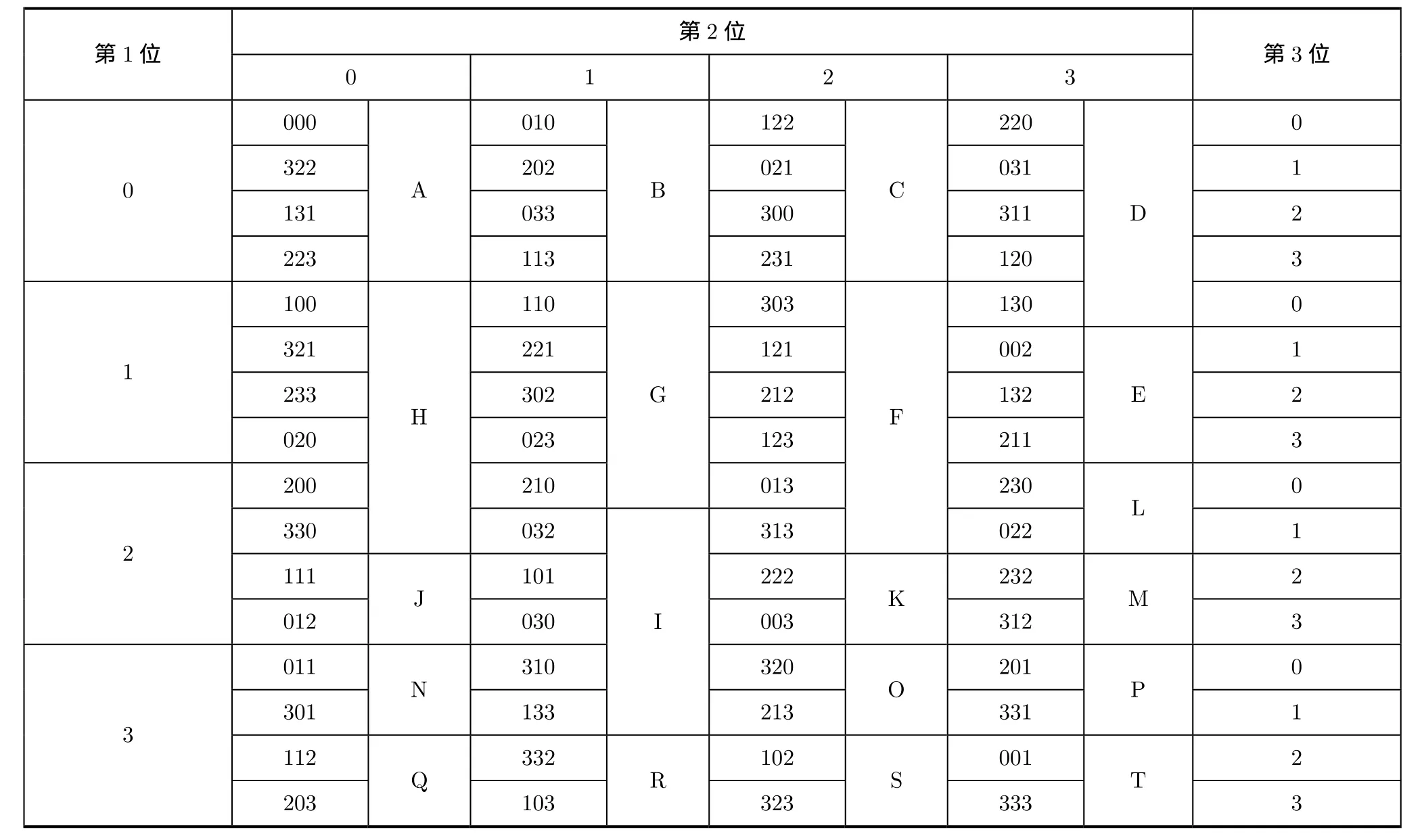
表3 构造密码子分组表
相对于一般的混沌系统,文献[12]提出的超混沌系统具有更好的随机特性,下边采用该非线性超混沌系统来产生随机序列,并实现有关操作。首先迭代超混沌系统式(1)0N 次:可以得到 4个迭代序列 yk, k = 1 ,2,3,4,当 a =36,b= 3 ,c = 2 8, d = - 1 6, - 0 .7 ≤ k ≤ 0 .7时,非线性系统式(1)是超混沌的。然后将4个随机有理数序列整合:

最后利用整合后的有理数随机序列()x j构造最终的符合要求的随机数序列:

一段编码成密码子的序列可以根据分组表形成一种任意进制数制系统。假设该数制系统的基数序列为 P = { Pi,i = 1 ,2,… ,m },那么每个基数对应的数码序列为[0 ~ Pi-1],不同位的位权为。用一个例子来说明该任意进制数制系统,如图 1所示。该段密码子序列为{000,111,121,201,112,002},形成的任意进制数制系统中,基数序列分别为{4,2,6,2,2,3},每个基数对应的数码序列分别为0~3,0~1, 0~5, 0~1, 0~1, 0~2,如果假设左边为高位,右边为低位,那么从左至右各位的位权依次为{144,72,12,6,3,1}。
2.3 任意进制数制系统
3 加密与解密方案
首先将待加密的信息编码成密码子序列,然后根据加密控制信息以及密码子分组表来替换相应的密码子,从而实现加密。其中加密控制信息需要根据任意进制数制系统进行编码转换。具体的加密算法为:
(1)将待加密的数字媒体T解码成二进制序列B,然后根据第 2.1小节提出的编码方案编码成DNA核苷酸序列,并将三位核苷酸一组编码成密码子序列C;
(2)构造分组表,并利用密码子序列C和分组表构造出类似图 1所示的任意进制数制系统,为了处理方便和防止计算溢出,可以先将密码子序列分成小段然后再操作;
(3)采用第2.2小节的方案产生混沌符合任意进制数制系统的随机序列,构造替换规则:根据任意进制系统的当前位的基数,也即当前待替换的编码密码子()C i所属分组中密码子的数目,来确定对应的任意进制数制系统的当前位基数()D i,从而形成任意进制的数制系统下的任意进制数列A;

图1 任意进制系统以及密码子替换过程
(4)根据随机控制信息,也即任意进制数列A,替换密码子序列C中的密码子,替换后的密码子序列中第i的元素: C '(i) = M ( i, j'),参见图 1,其中j' = mod(j + A( i),D ( i)), A( i)为控制加密的任意进制数列的当前位,D( i)为任意进制数制系统当前位的基数;
(5)完成替换后的密码子序列重新编码成原始媒体的形式。
密钥的构成:选择何种DNA编码序列(表 1),可以用3位二进制数编码[o pq], o, p, q ∈ { 0,1}来标记8种序列中的一种,记作key1;用于构造置乱密码子分组表的随机分组数组Y时所需的混沌随机系统的参数:混沌初值 [y1, y2, y3, y4],混沌参数 a2=36,b2= 3 , c2= 2 8, d2=- 1 6, k2= z ,记作key2,其中 - 0 .7 ≤ z ≤ 0 .7;密码子序列控制信息产生时所需的混沌随机系统的参数:混沌初值 [y', y', y', y'],混
1234
沌参数 a3=36, b3=3, c3= 2 8, d3=-1 6, k3= z ',记作key3,其中 - 0 .7 ≤ z '≤ 0 .7。
解密方案的实现基本上是加密的逆过程,具体方案为:
(1)根据 key1将密文按照与加密时同样的思路进行编码,形成替换后的,也即加密后的密码子序列C′;
(2)根据 key2产生密码子分组数组Y,然后根据第2.1小节的方法构造置乱密码子分组表;
(3)根据密码子序列C′和置乱密码子分组表生成任意进制数制系统;
(4)根据 key3,结合步骤(3)的任意进制系统,产生解密任意进制的控制信息序列,该信息与加密时的控制信息相同,均为A;
(5)根据控制信息()A i和当前密码子()C i′以及任意进制数制系统,替换当前密码子以解密:C( i) = M ( i, j ),其中 j = mod(j' - A( i) , D ( i)), A( i)为控制加密的任意进制数列的当前位,D( i)为任意进制数制系统当前位的基数;
(6)替换后的密码子序列重新解码组成原始媒体的形式。
从上边的加密与解密过程可见,方案中有两次用到超混沌系统,这两次运用可以采用相同的初值与参量来简化密钥构造;当然,为了提高加密系统的密钥空间,一般两次运用时混沌系统的初值与参量选择不同而且不相关的数值。任意进制数制系统的构造受到编码和原始媒体介质的直接影响,因此每次的任意进制系统是不同的。此外,该加密方案可以实现一次一密。结合图 1,下面以表格的形式简洁地给出一个具体实现。图 1中箭头的方向代表加密替换密码子的方向,解密时方向相反。表 4中B代表待加密媒体解码后的二进制序列,B'为加密后的二进制序列,DNA代表编码成的DNA序列,DNA'为替换后的DNA序列,C为密码子序列,C'为替换后的密码子序列,D为任意进制系统当前位的基数,A为任意进制数制系统下的数列也即加密控制信息。整个实现将B加密成为B'。

表4 加密方案中的各种序列
4 实验与分析
本文提出的加密方案可以应用于各种数字媒体,只要它们是数字可编码的。下面的实验将所提出的方案应用于图像加密,选取图像每个像素的前三位最高有效位(3MSB)进行编码。当然,如果进一步提高加密强度,增大密钥空间,可以通过第 2.2小节提出的随机序列构造方案来随机选取每个像素用于编码加密的最高有效位的位数。从 USC-SIPI标准图像库中选择8位标准灰度图像进行了大量实验验证,通过 MATLAB 2012a在 Windows7 Ultimate Edition X64操作系统下进行仿真,计算平台为AMD Phenom (tm) ⅡX4 810处理器,2.6 GHz主频,4 GB内存。实验的具体实施和部分展示结果以及分析如下。
大小为512512×的8位灰度“Lena”图像的加密后与解密效果和一些性能指标以及与现有方案的比较结果在接下来展示。其中加密参量设定,也即密钥分别为,key1: [000]; key2: [12,2,9,1],a2= 3 6,b2= 3 ,c2= 2 8,d2=- 1 6,k2= 0 ; key3:[8,3,2,5], a2=36, b2= 3 , c2= 2 8, d2=-16,k2= 0 .2。加密与解密的基本效果如图 2所示,其中解密错误时的密钥设定为:在key1与key2相同的情况下,将 key3的初值改变 1 0-4也即key3':[8,3,2,5.0001], a2= 3 6,b2= 3 ,c2= 2 8,d2=-16,k2= 0 .2。而实际上,混沌系统对初值及其敏感,即使改变的更细微,整个混沌序列也会有很大的变化。加密之前图像的直方图和加密后的图像直方图如图3所示。通过这两个最常用的指标可见,本文提出的方案具有较好的基本加密效果。
对密钥空间进行分析,本文提出的加密方案涉及3个密钥:key1, key2和key3,其中key1有8种选择,key2和key3提供了4维超混沌系统的有理数序列,在文中混沌序列选取过程中,取每个有理数序列k位小数,在不考虑迭代次数限制和一些常量的选择时,可以大致计算密钥空间为:8× ( (10k)4)2,而一般k取13,14,15,因此足以抗现有计算体系下的穷举分析。而且,由于多次用到混沌系统,与一般的基于混沌系统的加密方案[6]相比,具有更大的密钥空间。关于密钥敏感性,如前面实验所述,由于所采用的超混沌系统本身对初值和参量具有特别强的敏感性,即使某一个参量变化仅为 1 0-10,也会造成混沌系统的巨大变化,从而影响到加密的最终结果,因此,方案对密钥足够敏感。

图2 标准Lena图像的加密与解密效果

图 3 标准Lena图像直方图和加密后的直方图
良好的加密方案应该具有较强的抗差分攻击能力,也就是说,当原始媒体仅仅改变很小时,加密后的结果应该具有很大的差异,一般通过像素数量变化率 (Number of Pixels Change Rate, NPCR)和归一化像素值平均改变强度(Unified Average Changing Intensity, UACI)两个指标来表现方案的抗差分攻击的能力。它们的计算公式:

随机选择“Lena”图像的一个像素值,并将其置零,然后计算两次加密后的NPCR和UACI值,经过20次计算,得到 NPCR和 UACI的平均值分别为99.6083%和32.95%,效果比较理想。本文提出的方案是一次一密的,而且借助于超混沌系统的强随机性和敏感性,足以抵抗差分攻击。
自然图像相邻像素之间具有较强的相关系,通过相关性可以分析出原始图像的一些统计特性,因此打破这种相关性是图像加密很重要的任务之一。相关性计算公式:

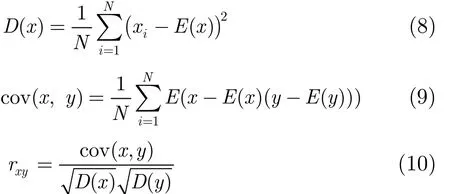
随机选择4096对像素水平方向、垂直方向和对角线方向上的相邻像素,将加密前后它们之间的相关像素值作图,可以发现,加密后图像相邻像素之间的相关性完全消失,见图 4。
信息熵是反应信息随机性的重要指标,加密后图像信息熵的理想值为8,其计算公式为

其中 P ( mi) 为 mi出现的概率,显然有= 1 。加密前后“Lena”图像的一组原始图像和加密后图像的相关系数与信息熵见表 5。可以发现加密后图像的相关性明显降低,信息熵基本趋向于理想值8。


表5 标准Lena图像加密后的参数
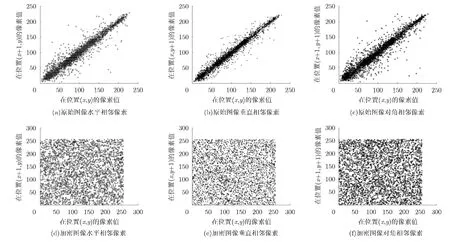
图4 标准Lena图像加密嵌入后相邻像素之间的相关性

表6 信息熵的比较

表7 UACI和NPCR的比较
本文方案有良好的加密效率,其编码过程与一般基于位面层次编码的加密方案中的编码过程类似,但置乱以及分组规则构造等耗时的运算则仅在构造密码子分组表的64个密码子上进行,大大降低了耗时运算的总量,在大规模数据加密过程中更具优势。在应用到图像加密的过程中,该方案仅选取图像的部分最高有效位编码,而非所有像素位面,因此加密基本操作的总量小。比如文献[9]中,操作的基本单位是图像的所有像素位面,而且加密过程需要进行多轮迭代,因此时间复杂度远高于本文方案。文献[4]通过 DNA编码和运算实现了基于位面层次的图像的加密。方案对图像所有像素位面进行编码操作,其两个核心操作是混沌置乱和 DNA加法。从基本操作的复杂性和总量上分析可见,本文提出的方案比文献[4]方案的基本操作总量小、复杂度低,具有更高的加密效率。将本文方案用于大小为256256בLena’ RGB彩色图像的加密,分别对3个通道进行加密后得到的信息熵与相关系数与文献[4]的加密方案的比较如表 8所示。可见本文方案在彩色图像的加密中取得较好效果,与文献[4]相比在加密后图像的抗差分攻击能力上有优势(UACI和NPCR值相对较高),主要原因在于编码与替换过程均引入混沌随机,而且每次加密的混沌密钥均不同。
5 结束语
运用分子生物学中 DNA编码和中心法则的思想,结合超混沌随机系统,本文提出了一种新的基于编码分组替换的加密方案。首先借鉴分子生物学中 DNA编码和中心法则的思想,将待加密媒体介质编码成密码子序列;然后设计一种替换方案对密码子序列进行替换从而实现加密。本文提出一种密码子置乱和随机分组方案,实现了较大差异密码子隶属于共同分组的情况,并将所构造的密码子分组作为密码子替换的依据。分组内的密码子替换由混沌系统来控制,较好地实现的加密。将本文提出方案用于图像加密,取得了较好的效果。方案是一种广义的加密方案,不仅可以用于图像加密,任何可编码的数字媒体都可以通过该方案实现加密。结合不同的数字媒体的自身特性,方案会取得更好的效果。

表 8 彩色Lena图像加密后的参数比较
[1] Shannon C E. Communication theory of secrecy systems[J].Bell System Technical Journal, 1949, 28(4): 656-715.
[2] Gao T and Chen Z. A new image encryption algorithm based on hyper-chaos[J]. Physics Letters A, 2008, 372(4): 394-400.
[3] Liu L, Zhang Q, and Wei X. A RGB image encryption algorithm based on DNA encoding and chaos map[J].Computers & Electrical Engineering, 2012, 38(5): 1240-1248.
[4] Wei X, Guo L, Zhang Q, et al.. A novel color image encryption algorithm based on DNA sequence operation and hyper-chaotic system[J]. Journal of Systems and Software,2012, 85(2): 290-299.
[5] Pareek N K, Patidar V, and Sud K K. Diffusion-substitution based gray image encryption scheme[J]. Digital Signal Processing, 2013, 23(3): 894-901.
[6] 朱从旭, 胡玉平, 孙克辉. 基于超混沌系统和密文交错扩散的图像加密新算法[J]. 电子与信息学报, 2012, 34(7): 1735-1743.Zhu Cong-xu, Hu Yu-ping, and Sun Ke-hui. New image encryption algorithm based on hyperchaotic system and ciphertext diffusion in crisscross pattern[J]. Journal of Electronics & Information Technology, 2012, 34(7):1735-1743.
[7] Tong X J. Design of an image encryption scheme based on a multiple chaotic map[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(7): 1725-1733.
[8] Teng L and Wang X. A bit-level image encryption algorithm based on spatiotemporal chaotic system and self-adaptive[J].Optics Communications, 2012, 285(20): 4048-4054.
[9] Zhang W, Wong K W, Yu H, et al.. A symmetric color image encryption algorithm using the intrinsic features of bit distributions[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(3): 584-600.
[10] Ye G. Image scrambling encryption algorithm of pixel bit based on chaos map[J]. Pattern Recognition Letters, 2010,31(5): 347-354.
[11] Crick F. Central dogma of molecular biology[J]. Nature, 1970,227(5258): 561-563.
[12] Gao T, Chen Z, Yuan Z, et al.. A hyperchaos generated from Chen’s system[J]. International Journal of Modern Physics C,2006, 17(4): 471-478.
[13] Liu H and Wang X. Image encryption using DNA complementary rule and chaotic maps[J]. Applied Soft Computing, 2012, 12(5): 1457-1466.

