同信道干扰条件下的多天线放大转发中继中断概率分析

李 敏 林 敏

1 引言

众所周知，应用多输入多输出（MIMO）技术可以提高无线通信系统的频谱效率和可靠性[1]，与此同时，无线中继技术能够用来改善无线网络的性能以及扩大覆盖范围[2]。因此，将MIMO和无线中继相结合构成的 MIMO中继技术成为未来无线通信系统标准中的核心技术[3]。在不同的中继协议中，放大转发（Amplify-and-Forward, AF）由于实现复杂度低而受到了广泛的重视。放大转发协议有两种实现方案：固定增益和可变增益[4]。假设信道状态信息（Channel State Information, CSI）已知，波束形成技术，尤其是发射端采用最大比传输（Maximal-Ratio-Transmission, MRT）同时在接收端采用最大合并比（Maximal-Ratio-Combining, MRC），作为MIMO中一种重要的实现手段被广泛应用于多天线无线通信系统中[5,6]。文献[6]研究了在发射端、中继端和接收端都配置多根天线的前提下，如何设计最优的波束形成方案来最大化接收端的信噪比（SNR）。文献[7]假设每条链路都采用发射天线选择/最大合并比接收（Transmit-Antenna-Selection/Maximal-Ratio-Combining, TAS/MRC）技术，推导了接收端信噪比的概率分布函数（Cumulative Distribution Function, CDF）和系统的平均误符号率（Average Symbol Error Rate, ASER）。文献[8]研究了MIMO AF中继系统在每条链路都采用波束形成技术的前提下，分析了反馈时延、信道估计误差和信道相关性对系统性能的影响。

在蜂窝通信系统中，由于采用频率复用技术，来自临近小区的同信道干扰（Co-Channel Interference, CCI）会严重降低系统的性能。因此，同信道干扰对中继系统的影响成为了近年来的研究热点。文献[9]推导了接收端受到同信道干扰条件下采用固定增益方案的中继系统的中断概率（Outage Probability, OP），文献[10]研究了中继端受到同信道干扰时采用可变增益方案的性能。假设只存在一个干扰且服从莱斯（Rice）分布，文献[11]推导了采用固定增益方案的系统性能。假设中继系统的信道服从Nakagami-m分布且中继端受到多个同信道干扰的影响，文献[12]分析了采用可变增益方案的系统性能。文献[13]推导了同信道干扰对中继系统容量的影响。虽然上述文献考虑了同信道干扰对中继系统的影响，但它们局限于发射端、中继端和接收端都采用单根天线的场景，而配置多根天线是未来无线通信系统的一个必然趋势，因此，研究多天线场景下同信道干扰对中继系统的影响具有更加重要的现实意义。其中文献[14-16]都研究了同信道干扰对采用波束形成技术的多天线中继系统的影响。假设中继端只受到一个同信道干扰和噪声的影响而接收端只有噪声时，文献[17]推导了固定增益中继系统的中断概率。文献[18]在文献[17]的基础上，还考虑了可变增益方案。但需要指出的是文献[17]和文献[18]只研究了中继系统的一个终端配置多根天线且只有一个干扰的情况，而当发射端、中继端和接收端同时配置多天线时，同信道干扰对双跳中继系统的影响是迄今为止仍未得到解决的技术难题。

本文的主要贡献是分析了存在多个CCI和噪声情况下的 MIMO AF固定增益中继系统的中断概率。首先在中继系统的发射端、中继端和接收端都配置多天线，而每条链路的发射端和接收端分别采用MRT和MRC技术，并且中继端受到多个同信道干扰的条件下，得到了接收端信干噪比（SINR）的表达式。接着同时考虑中继端和接收端噪声的影响，推导出中继系统的中断概率闭合表达式。最后计算机仿真验证了性能分析的正确性，并分析了天线数和干扰对中继系统的影响。文献[18]虽然考虑了干扰，但中继系统中只有一个节点配置多天线，而且只存在一个干扰。尤其需要指出的是，为了在数学上能够得到闭合表达式，文献[18]将多天线中继系统分成3种情况，而本文用一个更加通用的MIMO AF中继模型包含了这3种特殊的情况，因此不仅是文献[18]的简单推广，而且是多天线中继性能分析领域更深层次的研究。

2 系统模型

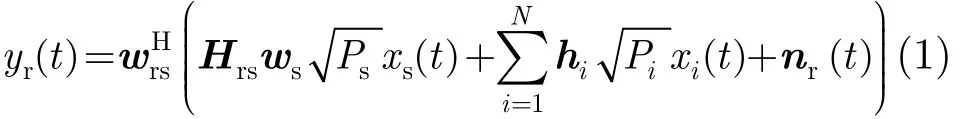
其中 Ps是发射信号的功率， Pi是第i个干扰发射的功率， hi（Nr×1）是从第i个干扰源到中继的瑞利信道矢量，其每个元素为独立同分布的复高斯随机变量且满足ℵC（0,1）。nr（t）（Nr×1）是中继端的噪声矢量，其每个元素为独立同分布的复高斯随机变量且满足 ℵC（0,）。在第2个时隙，中继端以增益G对信号 yr（t）进行放大后传输到接收端。中继端到接收端的信道矩阵 Hdr（Nd×Nr）的每个元素为独立同分布的复高斯随机变量且满足ℵC（0,1）。在中继端和接收端采用波束形成技术后，输出信号可以表示为

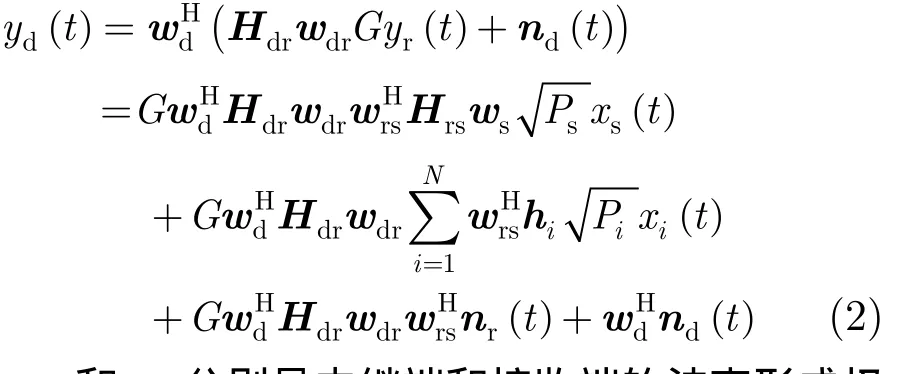
其中 wdr和 wd分别是中继端和接收端的波束形成权矢量。 nd（t）（Nd×1）是接收端的噪声矢量，其每个元素为独立同分布的复高斯随机变量且满足（0）。将式（2）代入式（1），输出的信干噪比可以表示为

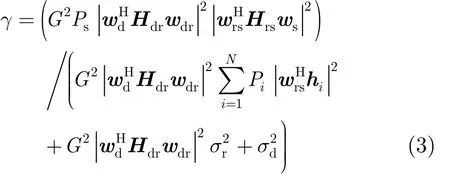
需要指出的是，文献[18]在只有一个终端配置多天线的情况下也推导出了类似的结果。因此，本文将文献[18]的工作推广到了一般的情况。

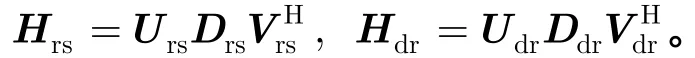
别是 Hrs的左奇异矩阵和右奇异矩阵。 Drs是Nr×Ns的矩阵，除了对角线以外其他元素都是零，其对角线元素是的特征值的平方根并以从大到小的顺序排列，表示为同 样， 酉 矩 阵 Udr=[udr,1udr,2…udr,Nd]和Vdr=[vdr,1vdr,2…vdr,Nr]分别是Hdr的左奇异矩阵和右奇异矩阵。 Ddr是除了对角线以外其他元素都是零的Nd×Nr的矩阵，其对角线元素是的特征值的平方根并以从大到小的顺序排列，表示为因此，每个终端的波束形成矢量可以表示为 ws=vrs,1, wrs=urs,1,wdr=vdr,1,wd=udr,1。将它们代入式（3），接收端的信干噪比可以表示为

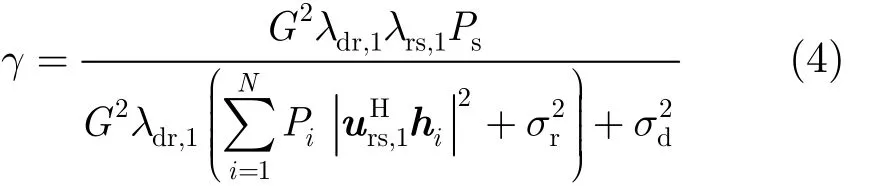
3 中断概率性能分析

本文采用固定增益方案，其增益G可以表示为

其中，rP是中继端的发射功率。由于满足ℵc（0,1），本文不难得到。为了推导的最大特征值λrs,1的均值，首先根据文献[20]得到λrs,1的概率密度函数（Probability Density Function, PDF）：

其中 Nrs=min { Nr, Ns}，系数 dp,q与发射端和接收端的天线配置相关。根据式（6），本文可以得出

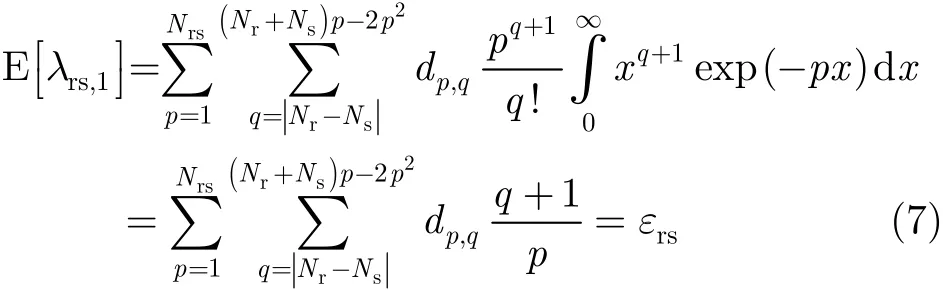
中断概率作为无线通信中衡量服务质量的一个重要指标，它定义为信噪比γ低于某一门限γth的概率

其中，Fγ（ z ）是 γ 的概率分布函数，可以表示为

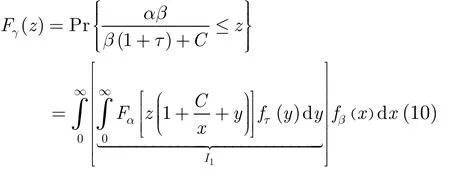
显然，推导出式（10）的关键是如何获得α的概率分布函数Fα（x ），β 和 τ的概率密度函数fβ（x ）和fτ（x）。为了达到这个目的，首先利用式（6）得到

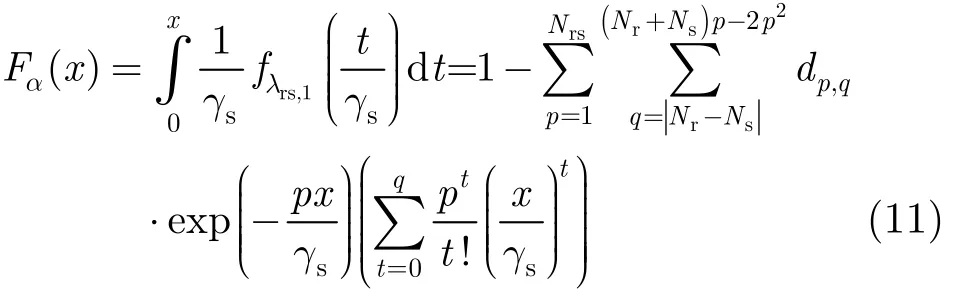
由文献[20]可知fβ（x ） 可以表示为

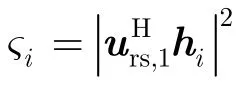
假设 γ1～ γN中有w个不同的值为 Ω1, Ω2,… ,Ωw，它们对应的重数分别为 m1, m2,…,mw，且满足=N ，那么式（13）可以用部分分式展开为

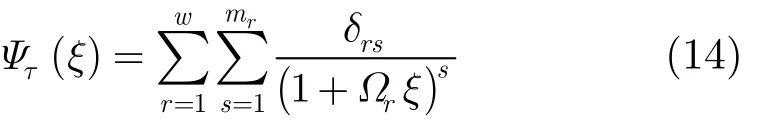
其中系数rsδ可以表示为

因此，对式（14）进行逆变换，可以得出fτ（ x ）的表达式：

将式（11）和式（16）代入式（10）中的1I ，经过相应的数学推导，可以得到

将式（12）和式（17）代入式（10），可以进一步得到

其中，对2I的计算首先进行二项式展开后并利用等式（文献[21], Eq. （3.471.9））得出。用thγ代替式（18）中的z就可以计算出采用固定增益的MIMO AF中继系统的中断概率。当中继系统的3个终端都采用单根天线且只有 1个干扰时，式（18）就简化成文献[11]中的式（12）。与此同时，当3个终端中的1个配置多天线且只有1个干扰时，按照不同的天线配置，例如：当发射端配置多天线时，发射端的波束形成方案采用MRT技术，式（18）可以简化成文献[18]中的式（5）；当接收端配置多天线时，接收端的波束形成方案采用MRC技术，式（18）可以简化成文献[18]中的式（13）。需要指出的是当中继端配置多天线时，由于文献[18]的中继波束形成方案采用的是一个量化的单位阵，没有采用本文的MRT和MRC技术，因此式（18）无法简化成文献[18]中的式（23）。

4 仿真结果

本小节通过计算机仿真来验证性能分析的有效性，分析天线配置、共信道干扰和功率分配对MIMO AF中继系统性能的影响。在所有的图中，标注（Ns, Nr, Nd）分别表示发射端、中继端和接收端天线的数量，代表共信道干扰的总干噪比。仿真中，信干噪比的门限设定为 γth= 0 dB，图1～图4中发射端和中继端的信噪比相等，即 γs= γr= γ 。

图1 不同天线配置下的MIMO AF中继系统的中断概率

图2 不同干扰功率下的MIMO AF中继系统的中断概率

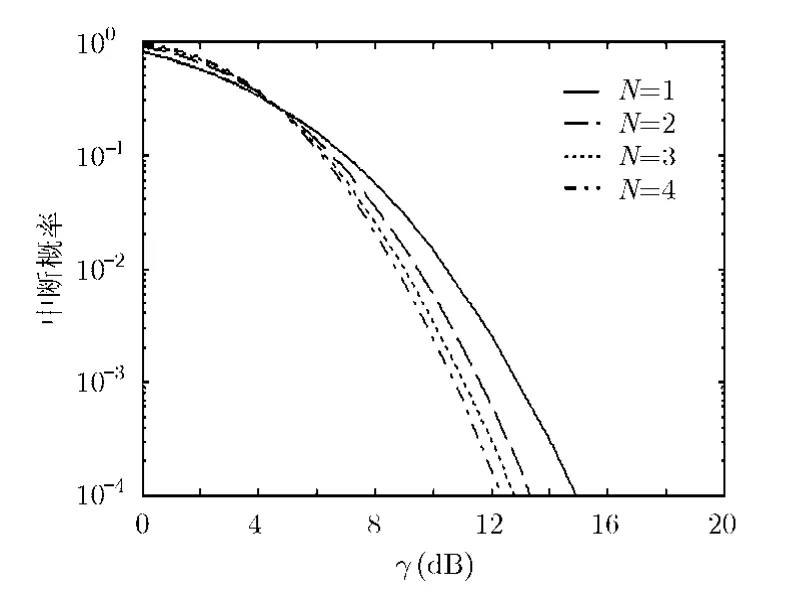
图3 不同干扰源数量下的MIMO AF中继系统的中断概率

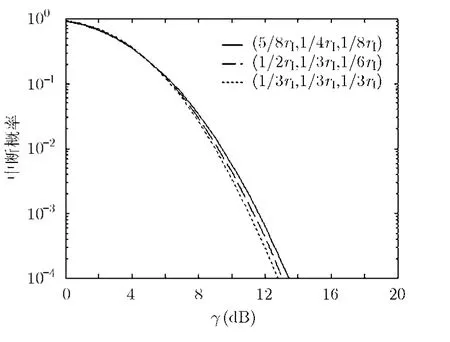
图4 不同干扰源功率分配下的MIMO AF中继系统的中断概率

首先，本文研究天线配置对系统性能的影响。假设存在 3个干扰，它们的干噪比分别是 5 /8γI，1/4γI和 1 /8γI，而总的干噪比为 γI= 1 0 dB。在天线总数量为8的情况下，考虑6种天线配置，分别 是 （6,1,1）, （1,6,1）, （1,1,6）, （4,2,2）, （2,4,2）和（2,2,4）。其中，前3种天线配置由文献[18]提出，后3种天线配置是本文研究的对象。可以看出，Monte Carlo仿真结果与性能分析结果完全一致，证明了本文提出的性能分析方法的有效性。从图1中可以看出，（1,6,1）的性能好于（6,1,1）和（1,1,6），这是因为（1,6,1）的每条链路都有6个信道，而（6,1,1）的第 2条链路和（1,1,6）的第 1条链路只有 1个信道，因此（1,6,1）能提供更多的分集增益。同理，（2,4,2）的性能好于（4,2,2）和（2,2,4）。另外，本文可以看出（6,1,1）的性能要优于 （1,1,6）, （4,2,2）的性能也要优于（2,2,4），这是由于同信道干扰存在于第 1条链路的接收端，因此第1条链路应该提供更多的分集增益来对抗干扰。最后，本文（2,4,2）的性能要优于（1,6,1），说明了天线数量受限的条件下在终端配置多天线能够带来性能的改善。

接下来，本文研究干扰对系统性能的影响。此处考虑 3 组天线配置：（4,2,2）, （2,4,2）和（2,2,4）, 2组不同功率的干扰： γI= 5 dB 和γI= 1 0 dB。在每组干扰条件下，干扰源数量和干扰源的功率分配都和图1一致。仿真结果如图2所示。与图1类似，Monte Carlo仿真与性能分析结果一致性证明了性能分析的有效性。在同一天线配置下， γI= 5 dB的性能要优于 γI= 1 0 dB 的性能，说明了干扰功率对系统性能的影响很大。更进一步，图3中还给出了干扰源数量对系统性能的影响。其中干扰的总干噪比为γI= 1 0 dB，干扰源的数量N为1～4，且每个干扰源均分干扰功率，天线配置为（2,4,2）。可以看出，只有一个干扰时系统性能最差，随着干扰源数量的增加，系统性能好转。这说明，从如何干扰MIMO AF中继系统的角度出发，干扰源数量越少，干扰效果越好。最后，天线配置是（2,4,2），存在 3个干扰，且总的干噪比为 γI= 1 0 dB的情况下，图4给出了干扰源功率分配对系统性能的影响。可以看出，等功率分配对应最好的性能。

5 结束语

本文研究了基于波束形成技术的双跳多输入多输出放大转发中继系统的中断概率，该系统在发射端、中继端和接收端都配置了多根天线。在每跳链路的发射端采用最大比传输技术，接收端采用最大合并比技术的条件下，我们得到中继端受到多个同信道干扰时的信干噪比，并进一步推导出基于固定增益中继方案的中断概率闭合表达式。最后，计算机仿真不仅验证了性能分析方法的有效性，而且还分析了天线配置、共信道干扰和功率分配对系统性能的影响以及配置多天线带来的好处。

[1] Hanzo L, El-Hajjar M, and Alamri O. Near-capacity wireless transceivers and cooperative communications in the MIMO era: evolution of standards, waveform design, and future perspectives[J]. Proceedings of the IEEE, 2011, 99（8）:1343-1385.

[2] Chen L, Huang Y, Xie F, et al.. Mobile relay in LTE-advanced systems[J]. IEEE Communications Magazine,2013, 51（11）: 144-151.

[3] Hoymann C, Chen W, Montojo J, et al.. Relaying operation in 3GPP LTE: challenges and solutions[J]. IEEE Communications Magazine, 2012, 50（2）: 156-162.

[4] Berger S, Kuhn M, Wittneben A, et al.. Recent advances in amplify-and-forward two-hop relaying[J]. IEEE Communications Magazine, 2009, 47（7）: 50-56.

[5] Kim J B and Kim D. Performance of dual-hop amplify-and-forward beamforming and its equivalent systems in Rayleigh fading channels[J]. IEEE Transactions on Communications, 2010, 58（3）: 729-732.

[6] Li M, Lin M, Yu Q, et al.. Optimal beamformer design for dual-hop MIMO AF relay networks over Rayleigh fading channels[J]. IEEE Journal on Selected Areas in Communications, 2012, 30（8）: 1402-1414.

[7] Yeoh P L, Elkashlan M, and Collings I B. Exact and asymptotic SER of distributed TAS/MRC in MIMO relaying networks[J]. IEEE Transactions on Wireless Communications, 2011, 10（3）: 751-756.

[8] Amarasuriya G, Tellambura C, and Ardakani M.Performance analysis of hop-by-hop beamforming for dual-hop MIMO AF relay networks[J]. IEEE Transactions on Communications, 2012, 60（7）: 1823-1837.

[9] Zhong C, Jin S, and Wong K K. Dual-hop system with noisy relay and interference-limited destination[J]. IEEE Transactions on Communications, 2010, 58（3）: 764-768.

[10] Suraweera H A, Garg H K, and Nallanathan A. Performance analysis of two hop amplify-and-forward systems with interference at the relay[J]. IEEE Communications Letters,2010, 14（8）: 692-694.

[11] Suraweera H A, Michalopoulos D S, Schober R S, et al.. Fixed gain amplify-and-forward relaying with co-channel interference[C]. Proceedings of the IEEE International conference on communications, Kyoto, Japan, 2011: 1-6.

[12] Al-Qahtani F, Duong T, Zhong C, et al.. Performance analysis of dual-hop AF systems with interference in Nakagami-m fading channels[J]. IEEE Signal Processing Letters, 2011, 18（8）: 454-457.

[13] Trigui I, Affes S, and Stephenne A. On the ergodic capacity of amplify-and-forward relay channels with interference in Nakagami-m fading[J]. IEEE Transactions on Communications, 2013, 61（8）: 3136-3145.

[14] Ding H, He C, and Jiang L-G. Performance analysis of fixed gain MIMO relay systems in the presence of co-channel interference[J]. IEEE Communications Letters, 2012, 16（7）:1133-1136.

[15] Phan H, Duong T Q, Elkashlan M, et al.. Beamforming amplify-and-forward relay networks with feedback delay and inter-ference[J]. IEEE Signal Processing Letters, 2012, 19（1）:16-19.

[16] Yang W, Cai Y, and Xu X. Interference-limited MIMO relaying systems over Nakagami-m fading channels[J].Electronics Letters, 2012, 48（11）: 660-662.

[17] Zhong C, Suraweera H A, and Yuen C. Outage probability analysis of dual-hop multiple antenna fixed-gain AF relay systems with interference[C]. Proceedings of the IEEE Wireless Communications and Networking Conference,Shanghai, China, 2012: 59-64.

[18] Zhong C, Suraweera H A, Huang A, et al.. Outage probability of dual-hop multiple antenna AF relaying systems with interference[J]. IEEE Transactions on Communications, 2013,61（1）: 108-119.

[19] Andersen J B. Array gain and capacity for known random channels with multiple element arrays at both ends[J]. IEEE Journal on Selected Areas in Communications, 2000, 18（11）:2172-2178.

[20] Dighe P A, Mallik R K, and Jamuar S S. Analysis of transmit-receive diversity in Rayleigh fading[J]. IEEE Transactions on Communications, 2003, 51（4）: 694-703.

[21] Gradshteyn I S, Ryzhik I M, and Jeffrey A. Table of Integrals,Series, and Products[M]. San Diego, CA: Academic Press, 6th Ed, 2000: 363.