用于调制宽带转换器压缩频谱感知的重构失败判定方法

郑仕链 杨小牛

1 引言

认知无线电频谱感知需要对很宽的频段进行频谱检测[1]。在 Shannon采样理论下，要瞬时覆盖宽频段往往需要多路模数转换器，硬件实现较为复杂。压缩采样（也称为压缩感知）则有望以低于 Nyquist采样率的速率完成宽频段采样[2]，因此，很多学者将压缩采样应用到宽带频谱感知中[37]-。目前针对模拟信号的压缩采样方式主要有两种：随机解调采样[8]以及调制宽带转换器（Modulated Wideband Converter, MWC）采样[9]。随机解调采样假设信号满足多音模型，而MWC采样的信号模型为多子带信号模型，与实际情况更为接近[10]。本文的研究针对MWC采样。

在 MWC采样应用于频谱感知方面，文献[11]中给出了一些实验结果，文献[12]将文献[11]的工作进行扩展，提出了一种更为详细的基于MWC采样的宽带频谱感知流程，并给出了仿真结果。文献[13]进一步讨论了MWC压缩采样后的循环平稳检测方法。压缩采样得以应用的前提条件是信号的稀疏性，MWC也不例外。将MWC采样应用于频谱感知的一个基本前提就是频谱的稀疏性，即只有很少一部分的子信道被主用户占用。一旦确定了MWC采样系统的参数，其所能接受的频谱稀疏程度也就确定。但是，由于无线频谱环境的复杂性，并不能保证待感知的频段一定满足MWC的稀疏度要求。因此，信号不稀疏的情况下，频谱感知结果无法保证正确，若相信该结果而利用“频谱空穴”，则会对主用户造成干扰。针对该问题，文献[14]提出了通过多个认知节点相互协作来判断重构是否成功。由于需要多个节点协作，增加了信息交互量和实现复杂度。本文则提出一种只需单个认知节点的MWC压缩采样重构是否成功的判定方法，认知节点自身通过连续两次重构结果之间的相关性来判断重构结果是否值得信赖（即稀疏度是否在 MWC采样系统的接受范围内）。本文方法无需节点间的协作，降低了信息交互负担，可以避免在信号不稀疏的情况下相信重构结果，因此能够降低对主用户的干扰，达到保护主用户的目的。

2 MWC压缩采样

MWC采样[9]框图如图1所示。具体来讲，信号x（ t）同时输入m个通道。在第i个通道，信号 x（ t）与周期为 Tp的混频函数相乘，接着通过一个截止频率为1/（2Ts）的低通滤波器，滤波后的信号以1/Ts的速率进行采样。由于1/Ts足够小，所以现有的商用ADC能用来完成采样过程。

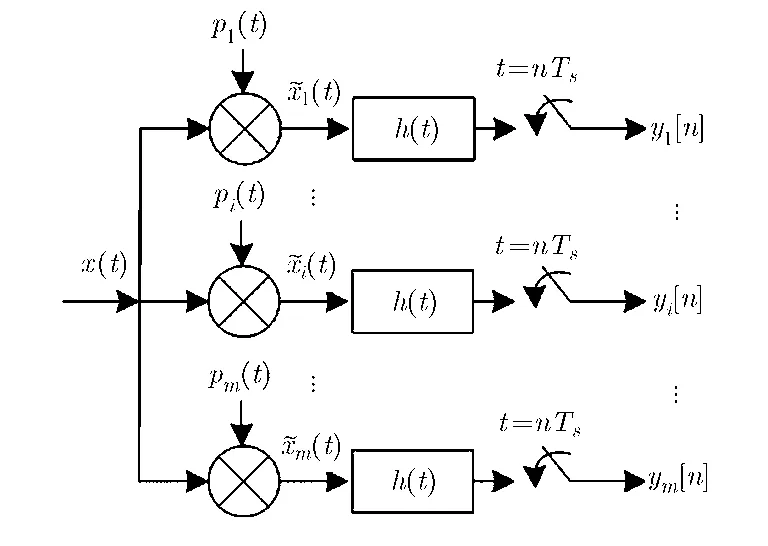
图1 MWC采样框图

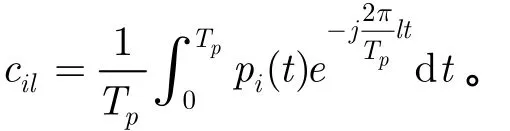
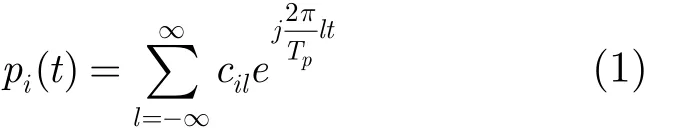
其中，考虑所有m个通

道，有式（2）形式的表达式成立[9]：

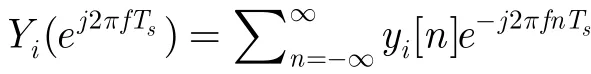
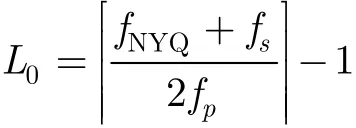
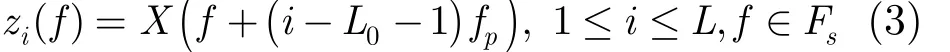
其中（）X f为（）x t的Fourier变换。mL×矩阵A第i行第l列元素ila 为

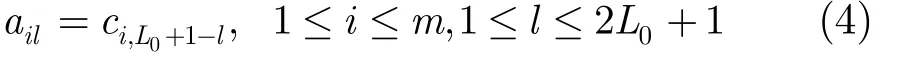
给定A和y（f），通过求解式（2），可以得到未知的z（f），再根据式（3）的关系式，可以求得原信号X（ f）。由于M＜L，所以式（2）所示的问题为欠定问题，当未知矩阵满足稀疏性条件时，可以采用压缩感知领域的重构方法来求解。

文献[9]中提出如下过程进行重构，首先计算：

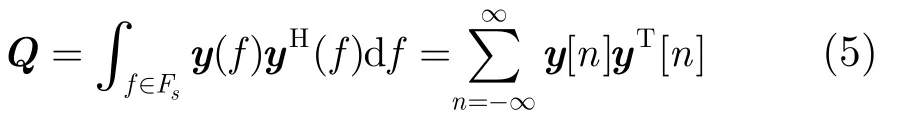
s通道采样构成的采样向量，然后得到满足 Q =VVH的矩阵V。接着通过求解 V = AU得到U的支撑S= s upp（U ） ，由于U的支撑与 z（ Fp） 相等，由此也就得到了 S = s upp（z （ Fp））。得到S后，就可以计算得到各个子带信号：

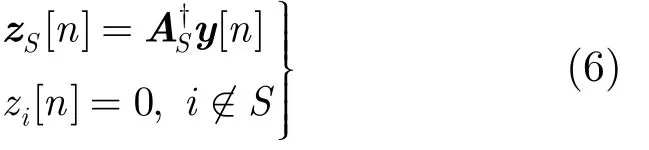
3 重构失败判定方法

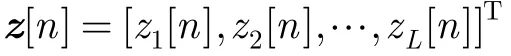
本文提出判断重构成败的方法基于频谱环境相对于重构时间来说是慢变的基本思想，由此，如果重构成功，那么相邻两次重构得到的信号的频谱应该非常接近一致，对应的各个子带信号的能量也应该接近一致；而如果重构失败，那么由于算法的随机性，相邻两次重构得到的信号的子带能量会有很大差别。因此，可以利用连续两次重构所得信号子带能量之间的相关性对重构成败进行判决。

设 S1和 S2分别表示连续两次重构得到的支撑，z（1）[n]和 z（2）[n]分别表示连续两次重构得到的子带信号。计算各个子带能量：

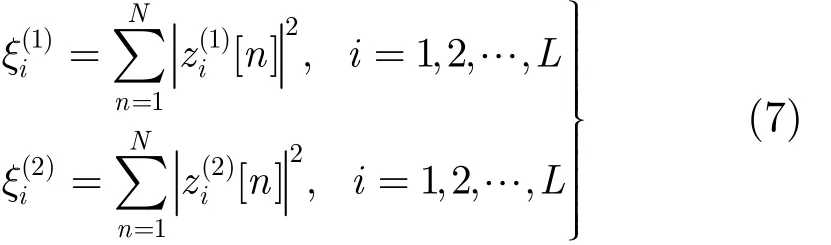
接下来计算判决统计量：

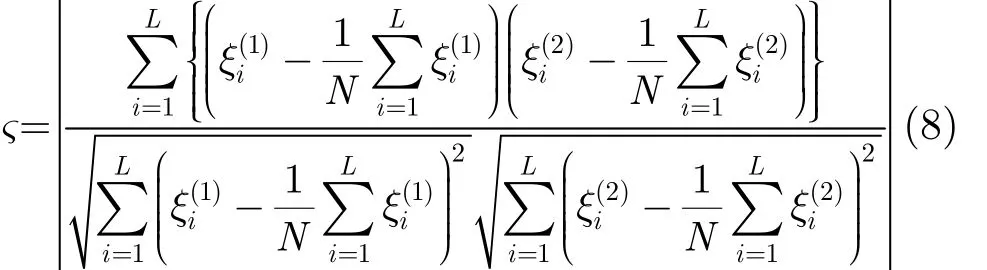
综上所述，本文提出的MWC压缩采样重构成败的判定方法流程如下：

Q = VVH的矩阵V，求解 V = AU得到U的支撑S1= s upp（U ） ，按式（6）计算得到子带信号 z（1）[n]；

步骤 4 根据式（8）计算得到判决统计量ζ。如果ζγ＞，判定重构成功（对应于信号稀疏），否则，判定重构失败（对应于信号非稀疏），γ为判决门限。

经过以上步骤，如果判定重构失败，则认为频谱感知结果不可信，认知用户不利用任何频谱空穴，以避免对主用户造成干扰。如果判定重构成功，则相信频谱感知结果。

本文方法依赖于相邻两次重构结果，从重构计算复杂度上来看，是单次重构方法的两倍。除重构之外，本文方法还需要式（7）所示的能量计算和式（8）所示的相关运算，计算复杂度为（）O NL。

4 仿真结果分析

仿真参数设定如下：信号频段 0～525 MHz,m= 4 0, fs= fp= 6 MHz。这种参数配置下，MWC系统总的采样率为 240 MHz，远远低于Nyquist采样率1050 MHz。仿真中，支撑重构算法考虑求解多观测向量模型的正交匹配（Orthogonal Matching Pursuit, OMP）算法[15]以及聚焦欠定系统求解法（FOCal Underdetermined System Solver,FOCUSS）[16]两种方法。主用户信道数目为87，各个信道上的主用户信号为BPSK或QPSK调制的通信信号，码速率共有4种取值可能：1.5 ksps（symbol per second）, 2.0 ksps, 2.5 ksps和 3.0 ksps。基带成型滤波器采用升余弦滤波器。整个频段上的信号信噪比固定为30 dB。

图 2中直观给出了两种情况下（稀疏和不稀疏）两次重构得到的各个子带能量，其中图2 （a）中信号个数为4，图2（b）中信号个数为20。由图2可知，当信号个数为4时，满足频域稀疏条件，两次连续重构得到的信号子带能量非常接近，其相关性达到了0.9990；而当信号个数为20时，已经超出了重构所能支持的稀疏度，因此两次连续重构得到的信号子带能量差异较大，相关性仅为0.7526。由此可知，两次连续重构所得子带能量之间的相关性可以反映重构是否成功。

图 3给出了本文方法对重构成败的判断准确率，其中判决门限γ设定为 0.993，图中同时给出OMP重构概率。判断准确率由本文方法判断重构成败结果与第 2次重构实际成败的比对得到，即第2次实际重构失败且本文方法判定重构失败的概率与第2次实际重构成功且本文方法判定重构成功的概率之和。第2次重构实际上是否成功采用支撑集来衡量：重构所得的支撑集合中包含所有被占用的信道标号，则实际重构成功，否则，实际重构失败。图3中重构概率即按照第2次重构实际成功的次数与仿真次数（本实验中为500）的比值来描绘。由图3可知，随着主用户信道占用数目的增加，频谱变得越来越不稀疏，因此，OMP重构概率越来越小。在信道占用数目为15和16附近时，本文方法对重构成败的判断准确率有所降低，这是因为在信道占用数目为15和16附近时，重构概率在0.5附近，实际重构成败的不确定性最大，前后两次重构结果成败的不一致性也最大，而由于本文重构成败的判定方法依赖于前后两次重构结果的相关性，因此导致其准确率降低。在信道占用数目较小（例如小于 10）或较大（例如大于 20）时，本文方法对重构成败的判断准确率都非常接近于 1，说明了本文方法的有效性。

图4给出了不同门限下本文方法对重构成败的判断准确率，采用 OMP方法。由图可知，判决门限的选择对判断准确率有影响，其值选择太小会造成判断准确率的降低，但也不能选择过大，太接近1会导致在信号不稀疏时判断不准确。从图4中结果可以看出，0.995是较为合适的选择。图5给出采用 FOCUSS方法作为重构方法时本文方法的判断准确率，判决门限采用0.995。从中可以看出，性能与OMP情况相当。

图6给出了利用频谱感知结果造成的对主用户的干扰概率，采用 OMP算法作为重构方法，FOCUSS的结果类似，为了简洁起见，在此省略其结果。干扰概率定义为被干扰的主用户信道数与总的被占用的主用户信道数目的比值。由图6可知，本文方法很好地避免了对主用户的干扰，对保护主用户的正常工作来说具有重要意义。

图2 子带能量

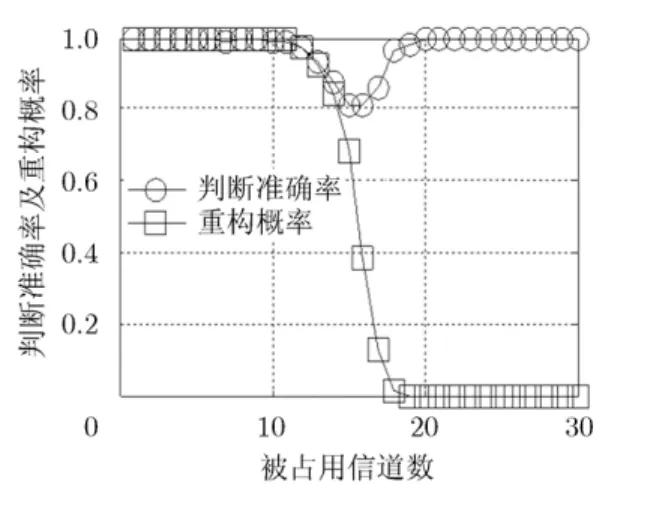
图3 判断准确率及重构概率（OMP）

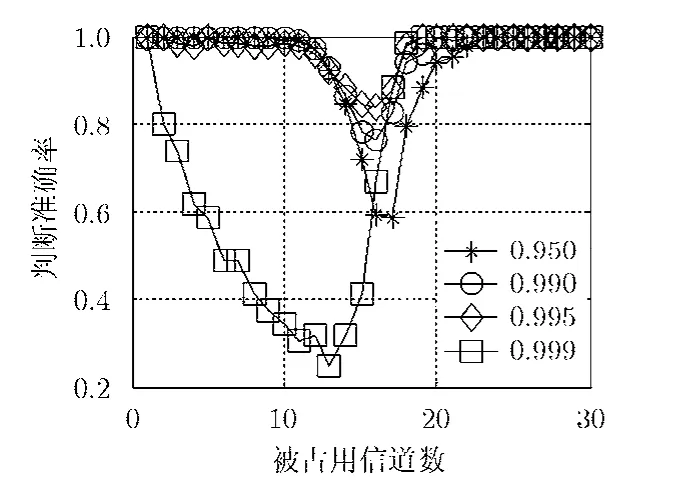
图4 判断准确率（OMP）

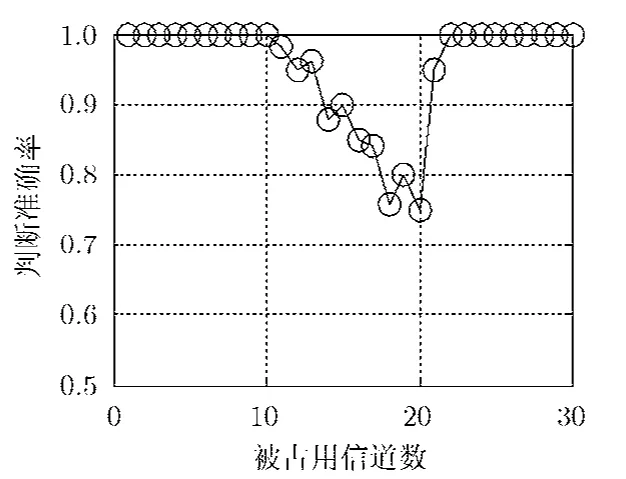
图5 判断准确率（FOCUSS）

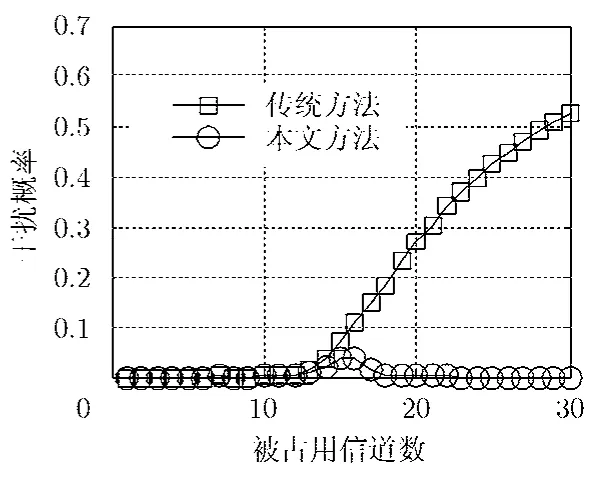
图6 主用户干扰概率

5 结束语

MWC压缩采样应用于频谱感知的一个前提是信号在频域上的稀疏性。如果信号不稀疏，将导致MWC重构结果不正确，此时若相信重构结果进而利用误判的频谱空穴，则会对主用户造成干扰。本文提出了一种判断MWC压缩采样重构是否成功的方法，以此解决认知无线电频谱感知应用中频谱不稀疏时重构结果不可靠导致的对主用户的干扰问题。仿真中采用了OMP和FOCUSS两种方法。结果表明在重构算法重构概率接近于1或接近于0对应的稀疏度区域，本文方法能够非常准确地判断MWC压缩采样重构成败，判断准确率接近1。在重构概率为 0.5附近对应的稀疏度区域，本文方法性能有所降低。另外，本文方法能够显著降低在频谱不稀疏时对主用户的干扰概率，从而达到保护主用户的目的。后续研究需要进一步改进重构概率为0.5附近对应的频谱稀疏度时的判断准确率。

[1] Sun H, Nallanathan A, Wang C X, et al.. Wideband spectrum sensing for cognitive radio networks: a survey[J]. IEEE Wireless Communications, 2013, 20（2）: 74-81.

[2] Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52（4）: 1289-1306.

[3] Tian Z, Tafesse Y, and Sadler B M. Cyclic feature detection with sub-Nyquist sampling for wideband spectrum sensing[J].IEEE Journal of Selected Topics in Signal Processing, 2012,6（1）: 58-69.

[4] Sun H, Chiu W Y, and Nallanathan A. Adaptive compressive spectrum sensing for wideband cognitive radios[J]. IEEE Communications Letters, 2012, 16（11）: 1812-1815.

[5] Yen C P, Tsai Y, and Wang X. Wideband spectrum sensing based on sub-Nyquist sampling[J]. IEEE Transactions on Signal Processing, 2013, 61（12）: 3028-3040.

[6] Romero D and Leus G. Wideband spectrum sensing from compressed measurements using spectral prior information[J]. IEEE Transactions on Signal Processing, 2013, 61（24）:6232-6246.

[7] Bai L and Roy S. Compressive spectrum sensing using a bandpass sampling architecture[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2012,2（3）: 433-442.

[8] Tropp A, Laska N, Duarte F, et al.. Beyond Nyquist: efficient sampling of sparse bandlimited signals[J]. IEEE Transactions on Information Theory, 2010, 56（1）: 520-544.

[9] Mishali M and Eldar Y C. From theory to practice:sub-Nyquist sampling of sparse wideband analog signals[J].IEEE Journal of Selected Topics in Signal Processing, 2010,4（2）: 375-391.

[10] Mishali M, Eldar Y C, and Elron A J. Xampling: signal acquisition and processing in union of subspaces[J]. IEEE Transactions on Signal Processing, 2011, 59（10）: 4719-4734.

[11] Mishali M and Eldar Y C. Wideband spectrum sensing at sub-Nyquist rates[J]. IEEE Signal Processing Magazine, 2011,28（4）: 102-135.

[12] Zheng S and Yang X. Wideband spectrum sensing in modulated wideband converter based cognitive radio system[C]. The 11th International Symposium on Communications and Information Technology, Hangzhou, China, 2011:114-119.

[13] Cohen D, Rebeiz E, Jain V, et al.. Cyclostationary feature detection from sub-Nyquist samples[C]. The 14th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, San Juan, Puerto Rico,2011: 333-336.

[14] Zhang Z, Li H, Yang D, et al.. Collaborative compressed spectrum sensing: what if spectrum is not sparse[J].Electronics Letters, 2011, 47（8）: 519-520.

[15] Tropp J and Gilbert A. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53（12）:4655-4666.

[16] Cotter S F, Rao B D, Engan K, et al.. Sparse solutions to linear inverse problems with multiple measurement vectors[J].IEEE Transactions on Signal Processing, 2005, 53（7）:2477-2488.