基于稀疏表示的高光谱数据压缩算法

吴 倩 张 荣徐大卫

(中国科学技术大学电子工程与信息科学系 合肥 230027)

(中国科学院电磁空间信息重点实验室 合肥 230027)

基于稀疏表示的高光谱数据压缩算法

吴 倩 张 荣*徐大卫

(中国科学技术大学电子工程与信息科学系 合肥 230027)

(中国科学院电磁空间信息重点实验室 合肥 230027)

如何降低高光谱图像大规模数据的存储和传输代价一直是学者们关心的问题。该文提出一种基于稀疏表示的高光谱数据压缩算法，通过一种波段选择算法构造训练样本集合，利用训练得到的基函数字典对高光谱数据所有波段进行稀疏编码，并对表示结果中非零元素的位置和数值进行量化和熵编码，从而实现高光谱图像压缩。实验结果表明该文算法与3维小波相比具有更好的非线性逼近性能，其率失真性能明显优于3D-SPIHT，并且在光谱信息保留上具有巨大的优势。

图像处理；数据压缩；高光谱遥感；稀疏表示

1 引言

高光谱遥感数据凭借其丰富的光谱信息而被广泛应用于环境监测、地质调查、资源勘探等领域。然而，考虑到此类多维大规模数据高昂的存储和传输代价，急需高效的压缩技术对数据进行编码。

国内外学者已经提出很多算法来解决这一问题。一般而言，高光谱遥感图像压缩算法可以分为两类：基于预测的无损压缩算法和基于变换的有损压缩算法。基于预测的无损压缩算法利用高光谱数据谱间相关性和空间相关性，通过特定的预测准则对当前像素进行估计并获取预测误差，如基于查找表的压缩算法及其相关改进算法[1- 3]。最近的一些无损压缩算法参考文献[4,5]。在有损压缩算法中，各种变换，如离散小波变换(DWT), KL变换等，被用来去除高光谱数据的谱间和空间冗余，然后对变换系数进行量化和熵编码[6]。由于小波变换良好的数学特性及相关的基于滤波器和提升框架的快速算法的提出，基于小波变换的编码技术在过去若干年处于统治地位[7- 10]。另外，由于PCA是最小均方误差意义下的最优去相关变换，JPEG2000具有最好的码率失真特性，PCA-JPEG2000[11]是目前最优的高光谱图像压缩方案，在低、中、高比特率下，都可以达到较为理想的压缩效果。近几年来，针对高光谱压缩领域的研究主要集中于低复杂度算法及高效编码方案的研究，同时有损压缩算法对数据信息的提取能力也更受到重视。文献[12]提出利用非线性PCA实现高光谱数据压缩和目标检测；文献[13]将视频编码标准H.264/AVC应用于高光谱图像，证明基于H.264/AVC方法设计低功率、实时的高光谱数据编码器的可能性；更多研究参见文献[14-17]。

然而，以上方法中所采用的固定的基函数对信号/图像的稀疏化表示能力有限，制约压缩比的进一步提高。与传统的固定正交基相比，一个通过训练得到的过完备的基函数字典可以更为稀疏地对信号进行表示。随着稀疏表示理论的发展，一些基于稀疏表示的算法被提出用于压缩自然图像和人脸图像[18]。考虑到高光谱数据极强的谱间相关性与结构相似性，将稀疏表示理论应用于高光谱图像压缩具有合理性。

本文提出了一种基于稀疏表示的高光谱数据压缩算法，利用一个通过训练得到的基函数字典对高光谱数据所有波段进行稀疏编码，并对表示结果中非零元素的位置和数值进行量化和熵编码，从而实现高光谱图像压缩。

2 稀疏表示理论

从某种角度来说，稀疏表示理论研究的是一个关于信号表示的数学模型。具体而言，对于信号x∈ℝn，其稀疏表示形式为

即信号x是字典中一系列原子{di}的线性组合，为各个原子对应的权重系数。

稀疏表示问题可以分为稀疏编码和字典学习两个部分。给定信号x和字典D，稀疏编码就是寻找稀疏解ω的过程，它可以表示为如式(3)所示的优化问题：

式(3)所示l0范数最小化问题为NP难题，通常采用贪心算法近似求解该问题，如正交匹配追踪(Orthogonal Matching Pursuit, OMP)[19]。与稀疏编码不同，字典学习用于估计基函数字典D。给定一个包含M个信号的训练样本集合字典可以通过求解下面的优化问题获得。

或

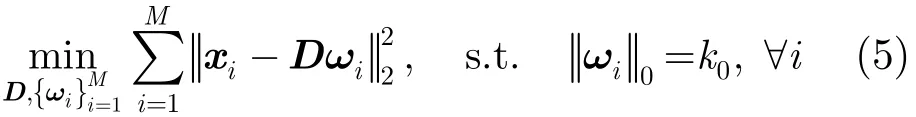
其中ε表示允许误差。简单地说，字典学习问题就是通过在字典D的基础上，寻找每一个样本xi最稀疏的表示系数ωi，以此获得对训练样本信号的合理表示结果，并得到所需的字典。字典学习算法多种多样，如奇异值分解法(K-SVD)[20]，递归最小二乘法(RLS)[21]，等等。

3 基于稀疏表示的高光谱图像压缩算法

高光谱遥感数据由同一地物对不同波长电磁波(可见光和近红外波段)反射成像而得，各波段之间具有很强的结构相似性，如图1所示。

根据稀疏表示相关理论，与所需要表示的信号相比，训练样本极具代表性，因而可以利用训练所得到的基函数字典对信号进行高效、稀疏表示。另一方面，对高光谱遥感数据而言，不同波段图像间存在很强的相关性与结构相似性，这使得利用高光谱数据某一波段数据作为样本训练得到基函数字典，然后对其他波段进行稀疏表示，并对稀疏表示系数进行熵编码以实现数据压缩。基于以上想法，本文提出了如下高光谱遥感数据压缩方案，包括：字典学习、稀疏编码和熵编码3个部分，如图2所示。

3.1 高光谱数据的稀疏表示方法

图1 AVIRIS Cuprite场景不同波段图像

图2 基于稀疏表示的高光谱遥感数据压缩方案流程

根据第2节字典学习理论，给定包含个L训练样本集合高光谱数据的字典可以通过式(6)所示的优化问题得到

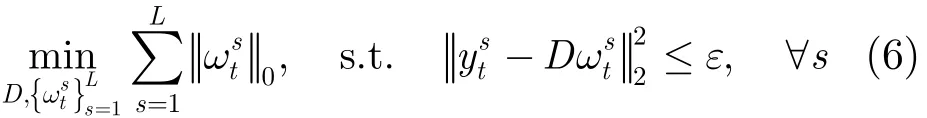
图3给出一个利用K-SVD[20]算法对AVIRIS (Airborne Visible/InfraRed Imaging Spectrometer)数据Cuprite场景进行学习得到的字典，图中字典大小为D∈ℝ256× 256。

图3 字典学习结果

3.2 训练波段选择

本文将稀疏表示理论应用于高光谱数据压缩，整个压缩流程中，需要选择一个合适的训练波段作为训练样本来进行字典学习。一种简单的做法就是随机选择一个波段作为训练集。然而，不同的训练波段对字典的表示性能会有不同的影响。对于某些波段，特别是大气吸收作用明显的波段，它们形似噪声，与其他波段相关性极低，如图4所示，如果选择这些波段作为训练波段，得到的字典的表示性能将不尽人意。

图4 Cuprite场景“噪声”波段

根据稀疏表示理论，当选择某波段作为训练样本时，字典学习问题是通过最小化重建波段和原始波段之间的逼近误差得到基函数字典。另一方面，稀疏编码是在给定稀疏度或允许误差的条件下根据训练所得的字典找到稀疏解。不难理解，训练波段与其需要用字典进行稀疏表示的波段之间相关性越高，训练得到的字典将具有更好的表示性能。因此，可以通过选择与其他波段相关程度最高的波段作为训练波段。

相关系数是衡量两个变量之间相关程度的指标。定义第k个波段和第k+s波段的相关系数为

其中σk, k+s为第k个波段和第k+s波段的协方差，σk和σk+s对应两个波段的方差，如式(9)和式(10)所示，为第k个波段的均值。

如3.1节所述，高光谱数据的表示是通过对波段图像分块进行的，考虑到不同图像块之间的关系，利用块相关系数对波段间的相关性重新定义：

表1 训练波段选择算法

值得注意的是，训练波段选择的目的是寻找一个可以接受的训练集，以保证训练样本具有一定程度的代表性，从而确保对高光谱数据稀疏表示的高效性。事实上，所得到的训练波段只是一个相对较优的选择，但不一定是最优波段。

采用AVIRIS数据Cuprite, Jasper Ridge和Lunar Lake, 3个场景第11～42波段数据图5所示的训练波段算法的性能进行验证。表2为几种不同准则组合下波段选择结果。其中C1和C2分别表示利用式(8)和式(11)计算相关系数。

由于高光谱数据相邻波段数据相关程度极高，几乎没有区别，结合表2数据，除了通过波段选择算法得到的训练波段之外，我们选取了其他若干波段作为训练波段，3个场景的率失真性能对比如图5所示。

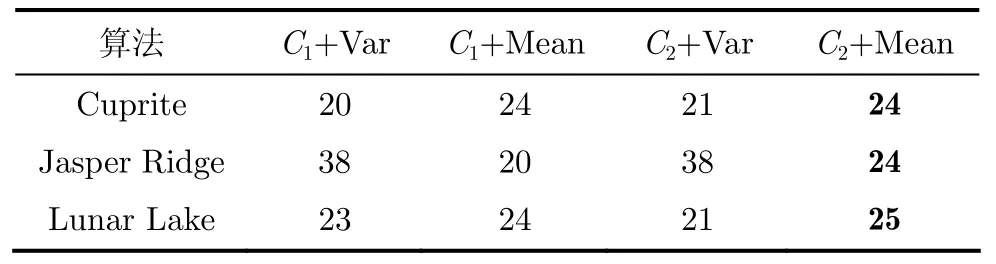
表2 波段选择结果

图5所示结果表明，经过不同训练波段学习得到的字典的率失真性能不同，其中C2+Mean的方式得到结果更为出色，并且计算简单。因此，我们建议采用C2+最大化相关系数均值的方式选择训练波段。

3.3 压缩方案

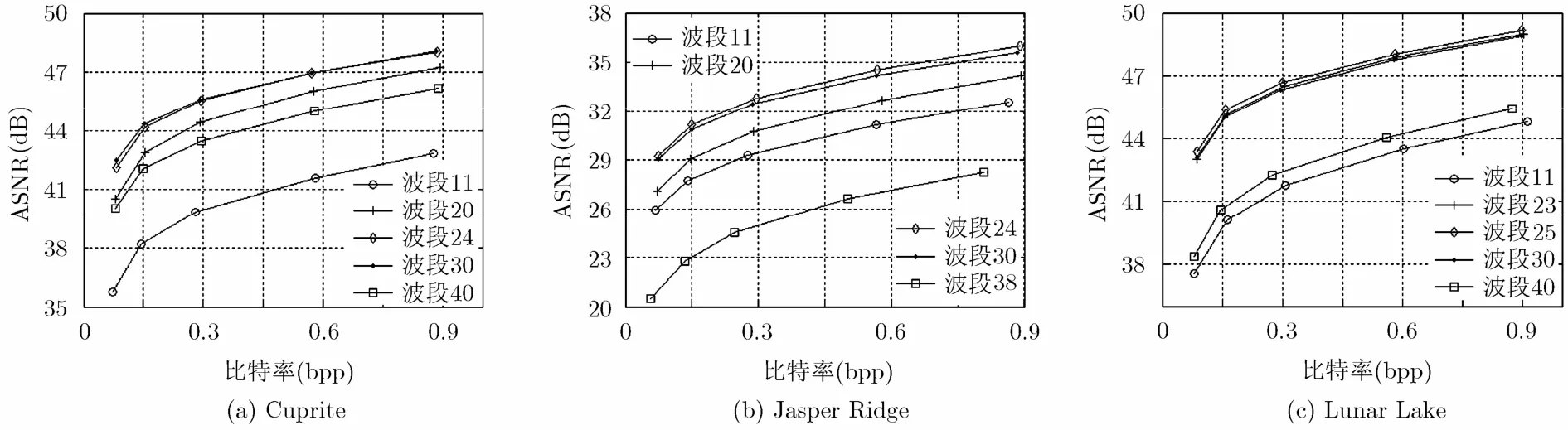
图5 不同训练波段情况下率失真性能比较

采用与前文相同的定义，假设稀疏编码后得到的稀疏系数矩阵为由于ω具有很高的稀疏性，即只有很少的元素为非零元素。那么，对于每一个数据块的稀疏解可用如下向量表示，其中分别表示第i个非零元素的位置索引值和数值，并且，由于对和的量化熵编码有两种方式：一种是按照中元素大小位置将和重排，对重排后的进行差分编码，对量化熵编码；另一种则是按照非零元素的赋值大小，即按中元素大小顺序对将和重排，对重排后的进行差分编码，对进行量化熵编码。对全部稀疏编码波段而言，最终的稀疏解为表示每个波段的稀疏解。

这里采用第1种方式对高光谱数据稀疏表示结果进行量化编码。对非零元素字典序数由于D∈ℝn× m, pi可能取到的最大值为m，那么，不考虑差分的影响，编码一个数据块所需的非零元素位置序号所需比特数为假设记录一个非零元素值所需的比特数为1，那么，整个压缩的比特率R为

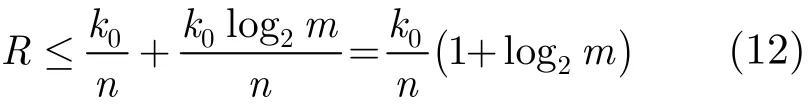
4 实验与分析

以下实验采用1997年AVIRIS的Cuprite，Jasper Ridge和Lunar Lake 3个场景的数据。AVIRIS图像包含224个波段，其宽度是614。为了方便起见，每个波段图像从左上角开始被切成512×512的子图像。本文实验中采用K-SVD训练字典，以下实验中所用字典D∈ℝ256× 1024，即字典包含1024个原子，波段图像分块大小为16×16。

4.1 压缩性能的评价指标

重构的图像的信噪比(SNR)通常被用作评价单一波段图像的压缩性能的标准之一。假设高光谱图像重建波段为第k个波段的信噪比定义为

对于高光谱数据，我们采用各重建波段的平均信噪比(ASNR)衡量整个算法的压缩性能：其中t为训练波段。

高光谱遥感技术最重要的应用之一是分类，其丰富的光谱信息可以用于识别不同类型的地物。从这个角度来看，对光谱信息的高保真重建是高光谱数据压缩需要满足的要求之一。光谱角是进行光谱匹配或高光谱数据分类的一个准则，它可以反映两条光谱曲线的相似程度。对两条光谱曲线其光谱角SA (Spectral Angle)定义为两个向量的夹角，如式(15)所示。

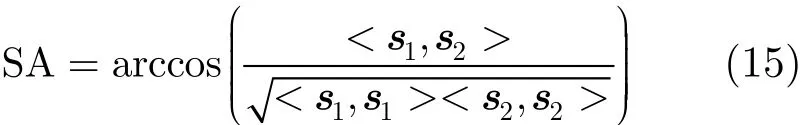
其中，＜·＞表示两个向量的内积。

这里用平均光谱角ASA(Average Spectral Angle)作为评价标准，定义如式(16)，以此来衡量压缩算法对高光谱数据光谱信息的保真程度。

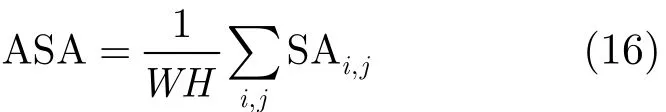
其中SAi, j表示空间位置为(i, j)的重建像元与原始像元之间的光谱角。

4.2 实验结果和讨论

4.2.1逼近性能比较 利用训练所得字典对高光谱数据进行稀疏表示，并与3维小波(3D-DWT)的逼近性能进行对比，结果如图6所示。图6中曲线为不同有效系数个数百分比(即保留的变换域系数的个数与全部系数个数之比)情况下对应重建图像的SNR曲线。其中3D-DWT采用9/7双正交小波基，分别进行3级分解(LEVEL 3)与5级分解(LEVEL 5)。

图6结果表明，在保留25%以内的有效系数时，稀疏表示方法的逼近性能优于3维小波的逼近性能，特别地，在仅保留少量系数的情况下，稀疏表示方法的逼近性能更为突出，这从侧面反映了字典学习表示算法在低码率压缩方面的优势。

图6 非线性逼近性能对比

4.2.2率失真性能比较 本节对不同压缩码率下稀疏表示压缩方案与3D-SPIHT压缩算法的压缩性能进行比较。图7显示了具体的压缩码率对比结果，图8为0.4 bpp情况下不同算法重建图像视觉效果对比。其中3D-SPIHT采用开源软件QccPack实现，采用9/7小波，对应的两条曲线中LEVEL 3和LEVEL 5分别表示算法中的3D-SPIHT所使用的小波分别进行3级分解和5级分解。本文算法里采用均匀量化的方式量化表示系数，并对其进行算术编码。实验结果表明本文算法明显优于3D-SPIHT，且对图像的结构信息具有更好的保真性能。

4.2.3光谱信息保留性能 为了评价压缩算法对高光谱数据光谱信息的影响大小，下面对不同比特率下重建数据与原始数据的光谱角进行对比，结果如表3所示。表3结果表明，基于稀疏表示的高光谱压缩算法在对原始光谱信息的保留方面具有巨大优势。图9给出了重建数据与原始数据光谱曲线对比。很明显，本文算法重建数据更贴近原始数据，对高光谱图像光谱信息的保留能力更强。

5 结束语

本文利用高光谱数据各波段的相似性，结合稀疏表示理论，提出了一种基于稀疏表示的高光谱数据压缩方案。实验结果表明，本文方案与以经典的3D-SPIHT算法相比，在中低比特率下具有巨大优势，并且本文算法可以更好地保留高光谱数据的光谱信息，对压缩后处理工作具有一定意义。由于稀疏表示算法具有较高的计算复杂度，其快速算法，特别是适用于高光谱数据的优化算法，是一个值得研究的方向。同时，与自然图像相比，高光谱图像具有更为复杂的结构特征，基于多尺度字典的压缩算法是未来需要研究的工作之一。

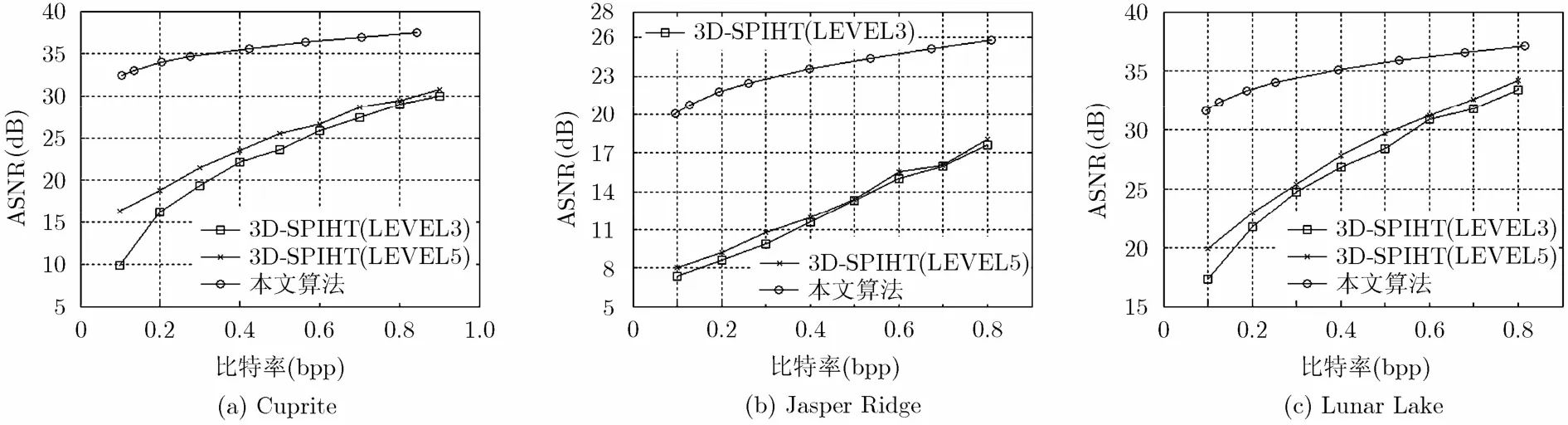
图7 率失真性能比较

图 8 不同算法重建图像视觉效果对比，各子图为0.4 bpp情况下不同算法Band 120的重建图像

表3 光谱角对比(°)

图9 重建图像光谱曲线对比

[1] Huang B and Sriraja Y. Lossless compression of hyperspectral imagery via lookup tables with predictor selection[J]. Remote Sensing, 2006, 63650L-63650L-8.

[2] Mielikainen J. Lossless compression of hyperspectral images using lookup tables[J]. IEEE Signal Processing Letters, 2006, 13(3): 157-160.

[3] Mielikainen J and Toivanen P. Lossless compression of hyperspectral images using a quantized index to lookup tables[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(3): 474-478.

[4] Mielikainen J and Huang B. Lossless compression of hyperspectral images using clustered linear prediction with adaptive prediction length[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(6): 1118-1121.

[5] Cheng K and Dill J. Hyperspectral images lossless compression using the 3D binary EZW algorithm[C]. SPIE Electronic Imaging, International Society for Optics and Photonics, 2013: 865515-865515-8.

[6] Penna B, Tillo T, Magli E, et al.. Transform coding techniques for lossy hyperspectral data compression[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(5): 1408-1421.

[7] Tang X and Pearlman W A. Three-dimensional Wavelet-Based Compression of Hyperspectral Images[M]. Hyperspectral Data Compression, Springer US, 2006: 273-308.

[8] Rucker J T, Fowler J E, and Younan N H. JPEG2000 coding strategies for hyperspectral data[C]. Proceedings of IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 2005: 1-4.

[9] Penna B, Tillo T, Magli E, et al.. Progressive 3-D coding of hyperspectral images based on JPEG 2000[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(1): 125-129. [10] Chang Chein-I. Hyperspectral Data Exploitation: Theory and Applications[M]. New York: John Wiley, 2007: 379-407. [11] Du Q and Fowler J E. Hyperspectral image compression using JPEG2000 and principal component analysis[J]. IEEE Geoscience and Remote Sensing Letters, 2007, 4(2): 201-205. [12] Du Q, Wei W, Ma B, et al.. Hyperspectral image compression and target detection using nonlinear principal component analysis[J]. SPIE International Society for Optics and Photonics, 2013: 88710S-88710S-6.

[13] Santos L, López S, Callico G M, et al.. Performance evaluation of the H. 264/AVC video coding standard for lossy hyperspectral image compression[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(2): 451-461.

[14] Wang C, Miao Z, Feng W, et al.. An optimized hybrid encode based compression algorithm for hyperspectral image[C]. International Conference on Optical Instruments and Technology (OIT2013), Beijing, China, 2013: 90451V-90451V-7.

[15] Cheng K and Dill J. Hyperspectral images lossless compression using the 3D binary EZW algorithm[J]. International Society for Optics and Photonics/SPIE Electronic Imaging, 2013: 865515-865515-8.

[16] Pan X, Liu R, and Lü X. Low-complexity compression method for hyperspectral images based on distributed source coding[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(2): 224-227.

[17] Noor N R M and Vladimirova T. Integer KLT Design Space Exploration for Hyperspectral Satellite Image Compression [M]. Convergence and Hybrid Information Technology, Berlin Heidelberg Springer, 2011: 661-668.

[18] Bryt O and Elad M. Compression of facial images using the K-SVD algorithm[J]. Journal of Visual Communication and Image Representation, 2008, 19(4): 270-282.

[19] Tropp J A and Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666.

[20] Aharon M, Elad M, and Bruckstein A. K-svd: an algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322.

[21] Skretting K and Engan K. Recursive least squares dictionary learning algorithm[J]. IEEE Transactions on Signal Processing, 2010, 58(4): 2121-2130.

吴 倩： 女，1988年生，博士生，研究方向为遥感图像处理、数据压缩.

张 荣： 女，1968年生，副教授，研究方向为数字图像处理、遥感图像处理、数据压缩.

徐大卫： 男，1990年生，硕士生，研究方向为遥感图像处理.

Hyperspectral Data Compression Based on Sparse Representation

Wu Qian Zhang Rong Xu Da-wei
(Department of Electronic Engineering and Information Science, University of Science and Technology of China, Hefei 230027, China)
(Key Laboratory of Electromagnetic Space Information, Chinese Academy of Science, Hefei 230027, China)

How to reduce the storage and transmission cost of mass hyperspectral data is concerned with growing interest. This paper proposes a hyperspectral data compression algorithm using sparse representation. First, a training sample set is constructed with a band selection algorithm, and then all hyperspectral bands are coded sparsely using a basis function dictionary learned from the training set. Finally, the position indices and values of the non-zero elements are entropy coded to finish the compression. Experimental results reveal that the proposal algorithm achieves better nonlinear approximation performance than 3D-DWT and outperforms 3D-SPIHT. Besides, the algorithm has better performance in spectral information preservation.

Image processing; Data compression; Hyperspectral remote sensing; Sparse representation

TP751.1

A

1009-5896(2015)01-0078-07

10.11999/JEIT140214

2014-02-19收到，2014-05-20改回

国家自然科学基金(61172154)，国家973计划项目(2010CB731904)，国家自然科学基金重点项目(61331020)和中国科学院光电研究院雏鹰计划资助课题

*通信作者：张荣 zrong@ustc.edu.cn