如何在教学中引导学生反思，以提高数学学习能力

李剑

摘 要：大多数学生在解决复杂问题时缺乏反思意识和反思能力，造成解题不完整或失误，形成数学难学的心理错觉。因此，引导学生正确反思，形成反思的意识和习惯尤为重要。在数学学习中我们要引导学生学会反思，积极反思，要充分调动学生求思的积极性和主动性，养成善于观察、分析、思考的学习习惯，提高学生发现问题和解决问题的能力。

关键词：引导反思；强化意识；优化思维；提高能力

学生学习数学的过程是一个完整的心智过程，在这个过程中，没有一个跌宕起伏的探究与调控的思维活动是难以完成的。大多数学生在解决复杂问题时缺乏反思意识和反思能力，造成解题不完整或失误，形成数学难学的心理错觉。因此，引导学生正确反思，形成反思的意识和习惯尤为重要。反思就是从一个新角度对问题及解决问题的思维过程进行全面的考察、分析、思考，从而深化对问题的理解，优化思维过程，揭示问题本质，探索一般规律，沟通知识间的相互联系；反思是一种积极的思维活动和探索行为，反思过程是主体自觉地对自己的认识活动进行回顾、思考、总结、评价和调节的过程；反思是同化、是探索、是发现、是再创造。通过反思可以拓宽思路、优化解法、完善思维过程；通过反思可以沟通新旧知识的同化和迁移，深化对知识的理解；通过反思可以提高科学意识，优化思维品质。

那么，怎样在教学中引导学生反思呢？下面谈谈我的体会。

一、 反思知识间的内在联系，促进知识的同化和迁移

数学学习过程是知识的同化和迁移的过程，反思是知识同化和迁移的推进器，通过反思可以挖掘知识间的内在联系，有利于帮助学生建立知识网络，教学中引导学生对例题、习题的结论进行反思，扩大和完善学生数学知识网络，丰富学生的元认知能力。

例1 求证：

（1）<2； （2）>2

（3）<4； （4）>1+

这组习题取自教材的例题、练习题、习题、复习题，师生共同完成第（1）题后，学生分组完成后3题，我们不能停留在学生会做这些题目上。

（1）上面四条不等式分别与下面四条不等式

①，②，

③，④等价吗（等价）。

（2）上述问题（1）中，各不等式左边两根式的被开方数之和与右边两根式的被开方数之和有何关系？（相等）

（3）问题（1）中各不等式左边两根式的被开方数之积与右边两根式的被开方数之积有何关系？（题（1）中，3×7<5×5；题（2）中，6×7>8×5；题（3）中，3×5<4×4；题（4）中，3×8>1×10）

（4）试找一找问题（1）中，各不等式的不等号方向取决于什么？（不等号方向取决定于不等式两边两根式的被开方数之积的大小）

（5）设a、b、c、d为正实数，若a+b=c+d，且ab>cd，由（3）（4）猜想与的大小关系如何？并证明你的结论。（>）证明略。通过以上设置问题，引导学生反思，挖掘这些不等式的内在联系，找出不等号取向的规律，使学生将教材习题的结论同化迁移得到一般性的结论，大大提升了学生解题能力。

二、反思思维过程，优化思维品质

在举例、训练、讲评数学问题时，倡导学生“一题多解、一题多变、多题一解”。我引导学生从不同角度考察问题时，摆脱固定的思维模式，注意反思思维过程的不足之处，完善思维过程，培养思维的严密性。答案做出来后，引导学生反思：“这种解法有漏洞吗？”。“能否做得更好一点？”通过反思，激发学生主动探索的欲望，努力探求解题的完整性，寻求最佳解题方法，促进元认知能力的发展，激发思维的创造性和灵活性。

例如，（2007广东韶关课改）解方程：

有的学生在去分母时，右边的1漏乘了，解完后只把答案代入最简公分母检验，就下轻易结论了，这时教师要提醒要知道解出的结果是否正确，可以代入原方程进行检验，促使学生反思哪一步出现了错误，找到失误所在，作出修改，从而进行总结，避免以后再犯类似错误。

通过对解题策略或解题方法的反思，寻求适用于某一解题方法的问题特点，从而把握解题的方法，确定正确、简捷的解题方法。

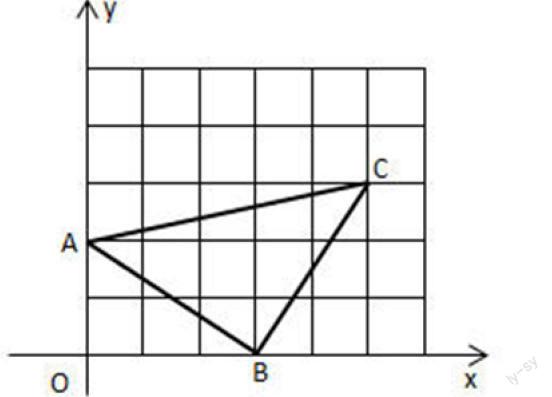
又如，如图小正方格边长为1，求△ABC的周长和面积。在求出面积后，鼓励学生多角度，多方向反思这个问题。

方法一：用矩形面积减去三个三角形面积。

方法二：用梯形面积减去两个三角形面积。

方法三：先证明△ABC为直角三角形，再求△ABC的面积。

方法四：过点C作CE⊥OX，证明△AOB≌△CEB，从而证

明△ABC为直角三角形，再求△ABC的面积。

方法五：过B点作BG⊥AC，利用等腰三角形的“三线合一”计算出BG的长，再求出△ABC的面积。

方法六：利用格点图形，设BC经过的格点为H，则△ABC面积应为△ABH面积的2倍。

学生的积极主动性调动起来了，创造意识也得到了培养。

三、强化反思意识，养成反思习惯

教学过程中，我们要把反思能力的培养贯穿于信息加工的各个环节，促进学生元认知水平的提高，让学生具备自我反思意识和养成良好的反思习惯，在教学过程中我们要抓好两条：一是指导学生经常进行自我诊断；二是创设情境让学生自我反思，真正做到通过学生自己的思考来学习数学。

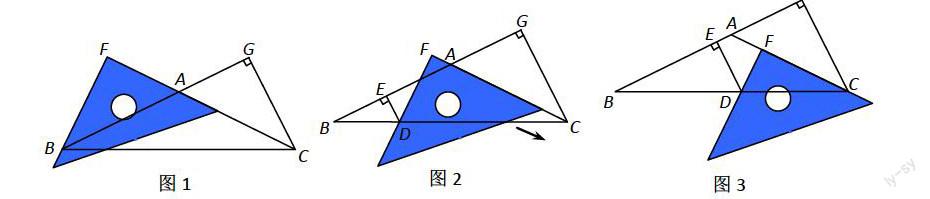
例如，（2007河北）在△ABC中，AB=AC，CG⊥BA交BA的延长线于点G，一等腰直角三角尺按如图1所示的位置擺放，该三角尺的直角顶点为F，一条直角边与AC边在一条直线上，另一条直角边恰好经过点B。

（1）在图1中请你通过观察、测量BF与CG的长度，猜想并写出BF与CG满足的数量关系，然后证明你的猜想；

（2）当三角尺沿AC方向平移到图2所示的位置时，一条直角边仍与AC边在同一直线上，另一条直角边交BC边于点D，过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG的长度，猜想并写出DE+DF与CG之间满足的数量关系，然后证明你的猜想；

（3）当三角尺在（2）的基础上沿AC方向继续平移到图3所示的位置（点F在线

段AC上，且点F与点C不重合）时，（2）中的猜想是否仍然成立？（不用说明理由）

在讲解这个题目时，我接着引导同学们，你能用一句话概括一下吗？（等腰三角形底边上一点到两腰的距离之和等于一腰上的高）。如果三角尺继续平移，结果会怎么样呢？接着给出：当三角尺在（3）的基础上沿AC方向继续平移到点F在线段AC的延长线上时，DF所在的直线与直线BC交于F，（2）中的猜想是否仍然成立？

猜想DE、DF与CG的数量关系。（DE-DF=CG）

反思并不是新思想，我国古代教育家就有反思意识，如“学而不思则罔，思而不学则殆”，“吾日三省吾身”等至理名言，强调了学与思的统一，注重学习后的反思，这些名言也对我们后人的学习产生了积极的影响。在数学学习中我们要引导学生学会反思，积极反思，要充分调动学生求思的积极性和主动性，养成善于观察、分析、思考的学习习惯，提高学生发现问题和解决问题的能力。