水下排气速度与温度场的气液两相流数值模拟
刘慧开,张劝华,赵小龙,王星宇,杨 立
(1.海军后勤部,北京 100036; 2.海军装备部,北京 100036;3.海军工程大学动力工程学院,武汉 430033)
水下航行器在通气管航态下,需要将发动机产生的高温废气排入海水中,废气进入海水将破裂成大小不一的气泡,气泡与海水混合形成具有复杂结构的气液两相流。为了掌握水下航行器通气管航行时水下排气的热特征,有必要对气泡在海水中的运动特性以及气泡与海水的气液两相流进行深入研究。当连续地将发动机废气排放到液体中去,由于气体自身的压力与周围环境压力的不平衡以及气液交界面上的表面张力等作用,气体将破裂成大小不一的气泡,在浮力力作用下,气泡将向上浮升。上升的气泡诱导周围的液体向上运动,形成气泡羽流流动[1-3]。对于气泡羽流的研究,国内外都开展了一些研究工作,但还很不成熟。1996年哈尔滨工程大学张文平[4]等利用摄像机拍摄和重放技术,观察研究了柴油机水下排气从管口到水面气液两相流动状态以及管口气泡形成、上浮和破碎的过程。发现整个两相流动状态可明显的分为气泡形成、自由气泡、气泡云以及水面喷涌4 个区域。气泡羽流的运动场通常可以划分为3 个区域:形成区、形成后区和表面流区。在形成区,气流破碎成气泡,并与环境液体混和,羽流宽度和轴线流速快速增长; 而形成后区羽流宽度和轴线流速的增加要缓慢得多; 在液体表面附近,羽流转向水平方向流动,形成具有垂向速度梯度的表面流区[5]。早期,国内外对气泡羽流的研究主要集中在实验研究和积分理论分析阶段[6,7]。近年来,对气泡羽流的数值研究逐渐增多,采用的数值方法主要有有限差分法、有限分析法和混合有限分析法。1994年林永明[8]等采用有限差分法对气泡羽流紊流场进行了数值分析和模拟,与Kobus 的实验结果符合较好。1999年Robert[9]基于完整的两相流模型对气泡羽流进行了二维和三维的数值模拟。2000年武汉水利电力大学的王双峰、槐文信[10]等从两相流理论中已被广泛接受的双流体概念出发,建立了描述两相湍流流动两方程模型,用于均匀环境中圆形气泡羽流的数值计算,所得结果初步证实了其正确有效性。2001年马霞[11]等假设气泡在水中的运动仅仅是一种紊动扩散现象,提出了一个预测圆形气泡特性的k-ε-E湍流模型,对静止环境中的圆形气泡羽流场进行数值模拟,模拟结果与实测资料吻合较好。2006年重庆大学刘洪涛[12]建立了气液两相流动传热的三维稳态数学物理模型,给出了描述不同模型下的换热及流动控制方程。2012年中国船舶研究中心的喻太君等[13]对水下冲压发动机喷管内的气液两相流进行了研究。
综上可知,前人对于静止环境中气泡羽流的速度场研究较多,而对于水下高温排气的气液两相流速度场和温度场的数值模拟研究几乎为空白。因此,有必要开展水下航行器水下高温排气的气液两相流数值模拟研究。本文通过建立水下排气的连续性方程、动量守恒方程和能量守恒方程,采用气液两相流混合模型和k -ε 紊流模型,利用有限体积数值计算方法,对水下排气的速度场和温度场进行了研究,得到了水下排气在海洋表面形成的温度分布,研究成果对水下航行器排气的红外抑制有重要的理论和应用价值。
1 水下排气的气液两相流模型
目前多相流研究通常有四种模型:Lagrangian 离散模型、欧拉模型(Eulerian Model)、VOF 模型和混合模型(Mixture Model)。模拟水下排气与海水热交换的速度场与温度场时,可以采用多相流中的混合模型。
连续性方程


能量方程

其中keff是有效热传导率,keff=k +kt,kt代表湍流热传导率。SE代表所有体积热源。
第二相体积分数方程

2 网格划分与数值计算方法
由于气液两相流模拟计算的复杂性,有必要对水下航行器排气口模型进行一定的简化。由于航行器外形主要对其后的流场产生扰动,而排气口大多布置在指挥台上,所以外形对排气与海水热交换所形成的温度场影响不是很大,本文忽略航行器外形对水下排气的影响。假设排气口半径为15 cm,航行深度为排气口距离水面4 m,计算区域海水温度为20℃。主流场采用笛卡尔坐标系:以排气口中心为坐标原点(0,0,0),排气管长0.5 m。其中y 轴正方向为尾流排气离开艇体的方向,y 轴负方向为航行方向,z 轴正方向为海水深度方向,主流场尺寸3 m×10 m×5 m,其数值计算实体模型如图1 所示。排气口采用四面体网格,在y =0 面采用三角形网格结构,流场区域采用混合网格结构。通过网格无关性检验,计算域共生成网格1 675 608 个网格单元,其网格划分情况如图2 所示。
利用Fluent 软件进行计算,通过3D 稳态分离求解器求解,重力方向为z 轴负方向,采用k-ε 紊流模型,定义海水为第一相,排气为第二相。主相、气相进口为速度边界条件,出口为Outflow,其他面为壁面条件。压力速度耦合格式为压力隐式分裂算子(PISO),压力采用PRESTO 分离,动量与能量方程采用QUICK 离散格式,相体积分数采用一阶离散方式。通过残差值检测器和两相进出口质量流量检测器来判断计算是否收敛,当残差值达到指定差值、两相进出口质量流量趋于相等时,认为计算已经收敛。
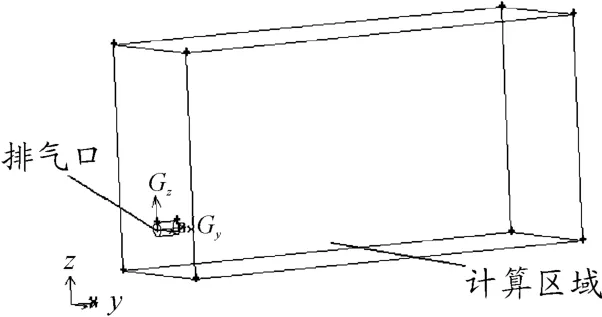
图1 数值计算实体模型

图2 网格划分
3 结果分析与讨论
3.1 排气速度场
图3 为中心轴线垂直纵截面上气相的速度分布图,由图可以看出水下排出气体在排气口大约7.5 m 处浮出水面。排气速度在排气口附近最大值为45.2 m/s,在离开排气口之后气体速度迅速减小,至排气口3 m 远时排气速度的最大值已经降至12.4 m/s,至浮出水面时气相速度基本上已经降至海水速度4.12 m/s。

图3 中心轴线垂直纵截面上气相的速度分布
图4为不同垂直截面上气相的速度分布,从图4 可以看出,离排气口由远及近,不同垂直截面上的气相速度逐渐减小,气相不断向四周环境水体中扩散,气相的分布区域逐渐增大,离排气口不远处的气体扩散表现为圆形扩散,后来逐渐扩散成马蹄形;每个截面都存在一个最大速度区域,且最大速度区域都位于扩散区域的中心区域。在y=0.6m 处,中心最大速度可达44 m/s,气体扩散至y =9m 处,速度降至4 m/s 左右,基本上已经达到海水的速度。

图4 不同垂直截面上气相的速度分布
图5为不同深度水平截面上气相的速度分布,从图5 可知,不同深度水平截面的气相速度分布都类似于“流星状”,“流星状的尾巴”在离开排气口的方向不断变宽,在“流星”的根部中心区存在一个最大速度,且越靠近水面,这个速度越小,当气相浮升至垂直高度4 m(浮出水面)时,气相速度基本已经降至海水的速度。在z =0 处,可以看到气体在排气口附近的最大速度为45 m/s,之后不断的衰减,形成明显的速度梯度。

图5 不同深度水平截面上气相的速度分布
综合图3 ~图5 可以发现排气在离开排气口之后速度迅速减小,排气在进入环境水体之后不断向水中扩散上浮,在浮出水面时,气泡速度已经降至环境水体速度。
3.2 排气温度场
图6 为中心轴线垂直纵截面上气相的温度分布,由图6可以看出水下高温排气在排气口大约7.5 m 处浮出水面,温度降至与海水的温差只有0.05 K。在排气出口烟气的温度为400 K,在离开排气口之后迅速减小,至排气口2.5 m 远时排气温度已经降至294 K。由于温度差异太大,为了能更好的表现出气体在浮出水面的温度场,图6 中的温度云图最大值为294 K,从中也可以看出气体在400 K 降至294 K 时所经历的时间是非常的短的。

图6 中心轴线垂直纵截面上气相的温度分布
从图7 可以看出,离排气口由远及近,不同垂直截面上的气相温度逐渐减小,气相不断向四周扩散,分布区域逐渐增大,离排气口不远处的扩散表现为圆形扩散,后来逐渐扩散成马蹄形,且每个截面都存在一个最大温度区域。对比图4,我们发现虽然温度场与速度场的变化有类似之处,但温度场的扩散区域要明显小于速度场扩散的区域,这说明温度的降低速率要比速度降低的速率要快得多。水下航行器排气在扩散至y=3 m 处时,其最大温度已经降至仅有293.5 K。

图7 不同垂直截面上气相的温度分布
图8为不同深度水平截面上气相的温度分布,从图8 可知,不同深度水平截面的气相温度分布都类似于“流星状”,“流星状的尾巴”在离开排气口的方向不断变宽,在“流星”的根部中心区存在一个最大温度,且越靠近水面,这个温度越小,当气相浮升至离排气口4 m(浮出水面)时,气相温度与海水的温度差降至0.05 K。对比图5,我们同样可以发现气泡的温度梯度要比速度梯度大很多,气泡从400 K 降至394 K 所需要的时间是非常短的。
综合图6 ~图8 可以发现:水下航行器排气在离开排气口之后温度迅速降低,气相温度在离开排气口水平距离3 m时,其最大温度已经降至仅有293.5 K;排气在进入环境水体后不断向水中扩散上浮,在浮出水面时,气泡温度已经降至与环境温度水体相差0.05 K;气相扩散的范围在刚离开排气口时基本为圆形,但是在浮出水面之后基本充满了整个计算区域。
3.3 不同排气温度下的水下航行器排气特征
在不改变其他初始条件下,改变水下航行器排气在排气口的初始温度,可以发现降低水下航行器排气在排气口的初始温度,可有效降低水下航行器排气浮升至水面时与周围海水的温度差。初始温度为523 K 的排气在离开排气口浮升至水面时,气相与周围海水的最大温差为0.11 K。当初始温度从523 K 降至400 K 时,浮升至海面时与海水的温度差从0.11 K 降至0.05 K,进一步降低初始温度至333 K 时,浮升至海面时与海水的温度差将降至0.013 K。可见,降低水下航行器水下排气口的初始温度,可有效降低排气浮升至水面时与周围海水的温度差。

图8 不同深度水平截面上气相的温度分布
4 结论
运用有限体积数值计算方法对水下航行器水下排气形成的气泡羽流的浮升过程进行了数值模拟,得到了水下排气形成的羽流速度场和温度场。
在温度均匀的海水中水下排气羽流浮升时,气相的速度不断减小,最后与海水的速度大小基本相等; 在气相速度减小的过程中,每一个纵截面都存在一个速度最大的中心区域,中心区域的形状由圆形慢慢发展成马蹄形。气相速度场的水平截面区域类似于“流星状”,且可看出明显的速度梯度存在。
水下排气羽流浮升时,气相的温度在海水中不断降低,由出口温度400 K 降至与海水的温差为0.05 K;在温度降低的过程中,每一个纵截面都存在一个温度最大的中心区域,中心区域的形状由圆形慢慢发展成为马蹄形;气相温度场的水平截面区域也类似于“流星状”,且可看出明显的温度梯度存在。与气相的速度场,温度场发展的区域要明显比速度场发展的区域“要窄”。
降低水下航行器排气的初始温度,可有效降低排气浮升至水面时与周围海水的温度差。当初始温度从523 K 降至400 K 时,浮升至海面时与海水的温度差从0. 11 K 降至0.05 K,进一步降低初始温度至333 K 时,浮升至海面时与海水的温度差将降至0.013 K。
[1]吴凤林,Tsang G.关于气泡羽流的研究[J].水动力学研究与进展,1989,4(1):104-112.
[2]吴凤林,Tsang G.三维气泡羽流建立区流动形态的观察[J].力学学报,1991,23(1):1-8.
[3]Friedl M J,Fannelop T K.Bubble plumes and theirs interaction with the water surface[J].Applied Ocean Research,2000(22):119-128.
[4]张文平,张天元,刘志刚,等.柴油机水下排气口气液两相流动状态研究[J].内燃机工程,1996,17(3):14-18.
[5]王双峰,槐文信,李炜.静止均匀环境中气泡射流特性的研究——数学模型及实验资料的分析[J].水科学进展,2000,11(1):25-31.
[6]Kobus H E.Proc.of 11th Conf.on coastal Eng[C].London,ASCE.New York,p 106,1968.
[7]Fannelop T K,Sjoen K.AIAA 18th Aerospace Sci.Meeting[C].Pasadena,CA.,1980.
[8]林永明,李炜.气泡羽流紊流的应力代数模型及数值分析[J].水道港口,1994,21(2):32-36.
[9]Robert F.Mudde,Oliver simonin.Two-and three-simulations of a bubble plume using a two-fluid model[J].Engineering Science,1999,54:5061-5069.
[10]王双峰,槐文信,李炜.静止均匀环境中气泡射流特性的研究——形成区及形成后区特性的数值研究[J].水科学进展,2000,11(1):32-37.
[11]马霞,李建中,魏文礼,等.气泡羽流的数值模拟[J].西安理工大学学报,2001,17(1):86-89.
[12]刘洪涛. 有内热源熔池内的气液两相流流动与传热[D].重庆:重庆大学,2006.
[13]喻太君,王宝寿.水下冲压发动机喷管内两相流动[J].四川兵工学报,2012,33(3):4-7.

