《几何证明选讲》在广东省高考中的常用题型分析

广东省广州市南海中学 纪丽敏

《几何证明选讲》有助于培养学生的逻辑推理能力。在几何证明的过程中，不仅有逻辑演绎的程序，还包含着大量的观察、探索、发现的创造性过程。

以下就广东省高考模拟题、高考题中出现的几何证明选讲选做题进行分析、归类，以期把握此类问题的常用题型，形抛砖引玉之效。

一、考察平面图形中基本的数量关系的理解和掌握

例1：在直角梯形A B C D中，DC∥AB,CB⊥AB,AB=AD=a,CD=

点E,F分别为线段AB,AD的中点，则EF=___

分析：题目中，出现点E,F分别为线段AB,AD的中点，学生很快会联想到三角形中位线定理，通过连接并计算BD，从而得出EF的长度。事实上，当我们连接DE，可知ΔAED为直角三角形，并且EF是RtΔDEA斜边上的中线，等于斜边的一半，为

这样不仅减少了计算，也体现了学生对题目中数量关系的把握和分析问题的能力。

二、应用相似三角形的判定和性质

例2：在平行四边形ABCD中，点E在AB上

且EB＝2AE，AC与DE交于点F，

分析：相似三角形面积比等于相似比的平方。

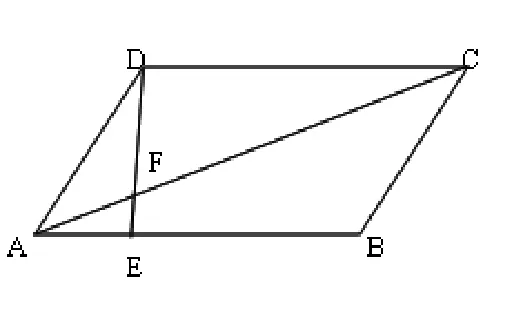
此类问题关键是证明三角形相似，然后通过对应关系解决问题。常用AA，AAA，三边成比例，两边成比例、两边夹角相等等基本方法。后例有有关三角形相似，计算其他比例值或长度。

三、考察同弧所对的圆周角、弦切角、圆心角的数量关系

例3：如图，过圆O外一点P分别做圆的切线和割线交圆于A,B两点，且PB=7，C是圆上一点使得BC=5，∠B AC = ∠APB ,则AB=___．

分析:本题是2011年理科高考题,看起来难度不大，但得分仅0.82,从得分看属于难题。事实上，由同弧所对的圆周角、弦切角相等，则∠PAB=∠ACB，又∠B AC = ∠APB,故△ABP∽△CBA，，AB=。

考察了同弧所对的圆周角、弦切角相等。题目中过P做圆的切线和割线，让一些不细心思考的学生陷入运用切割线定理的误区，导致不能得分。说明学生选择有效知识点并合理运用方面还不够好。

四、运用圆的相交弦定理

圆的相交弦定理是指圆内的两条相交弦被交点所分成的两条线段长的积相等。要注意强调是从交点出发的四条线段在同一弦的积。明显的特征是题目中出现圆内的两条弦相交。但并不是说出现了相交弦就一定会用到相交弦定理。

例4：如图，AC为⊙O的直径，OB⊥AC ，弦BN交AC于点M.

若OC=，OM=1，则MN的长为

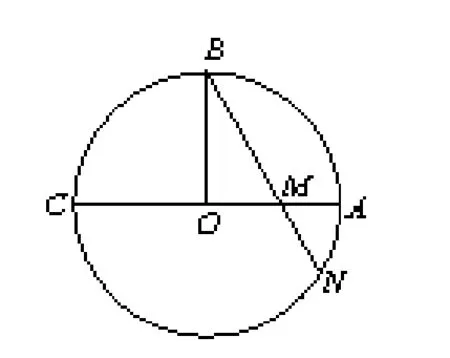
分析：由题OC=OB=，OM=1，则MB = 2 ,M A =− 1 ,M C =+1。

现在要求MN，很快由相交弦定理知:MN· M B =MA· MC, M N=1。

五、运用圆的切割线定理

例5：如图所示，过圆C外一点P做一条直线与圆C交于A,B两点，AB=2AP ,PT与圆C相切于T点.已知圆C的半径为2，∠CAB=30°，则PT=___

分析：PT为圆C的切线，由圆的切割线定理，PT2= P A⋅ PB，又A B=2 A P，P B=P A+A B，此时转化为如何求A B。在等腰△ACB中，AC=2，∠C_AB=30°，∴AB =,P A =,P B =。∴PT=3就迎刃而解了。

当题目中同时出现圆的切线和割线时，可以先考虑是否能利用圆的切割线定理解决问题。在运用圆的切割线定理时，一个比较容易错误的地方在于把定理写成PT2= P A⋅ AB 。和相交弦定理一样，都是从两条线的交点“发散”出去的线段，理解了这点就不容易写错、用错了。

六、运用直角三角形的射影定理

例6：如图，在圆O中，直径AB与弦CD垂直，垂足为E，EF⊥BC，垂足为F，若AB=6，CF⋅ CB=5，则AE=．

分析：要求AE，考虑到CE=ED，

AB与CD是圆的两条相交弦，AB又为直径且长度为6。

故怎样求CE是关键。

第一步：Rt△CEB中，由射影定理得CE2=CF⋅ CB =5。

第二步：由圆的相交弦定理得CE2=AE⋅ EB( = AE( A) B − AE )。

所以AE 6 − A E = 5 ,A E =1.

几何证明选讲选做题求解的关键在于找出连接条件与结论所有中间环节。既可以是从条件入手顺推，也可以是从结论着想逆推，还可以是两者结合。几何证明选讲选做题的条件和结论主要分两类：一类是度量关系，如相等、全等、成比例等；另一种是位置关系，如平行、共圆等，它们是相互联系、有机统一的。在近年的广东省高考模拟题、高考题中，考察有关几何证明选讲选做题的方式、方法相对明确，题型相对稳定。在实际的考试中，往往比较少的直接运用单一某个性质、定理，而是在这些性质、定理的基础上“拐拐弯”，运用多个性质、定理，以期达到教材编写者“希望通过本书的学习，让学生在知识积累、数学能力的提高、对数学的理解和认识等方面都能更上一个台阶的目的”。