谈区域问题的解题策略

河北省邢台市第二十六中学 郝晓辉

为了培养学生应用数学知识解决实际问题的意识和能力，高中课本当中引入了简单线性规划内容。本节内容主要是教给学生如何用图解法求线性规划问题的最优解，这也是本节重点难点所在。而用线性规划知识解决一些实际应用问题也较为方便快捷，因此线性规划问题在高考复习中就显得尤为重要，下面就举例说明一下线性规划及其实际应用。

一、平面区域的引入

二元一次不等式Ax+By+c＞0表示直线Ax+By+c=0的某侧部分，且不包括边界直线。而Ax+By+c≥0所表示的平面区域包括边界直线。

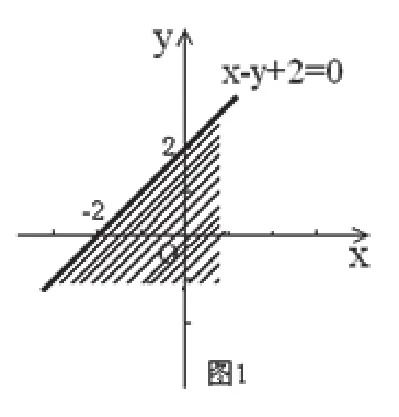
如x−y+ 2 ≥ 0表 示 直 线x−y+ 2 = 0及其下部，如图1，它是一个开放区域。

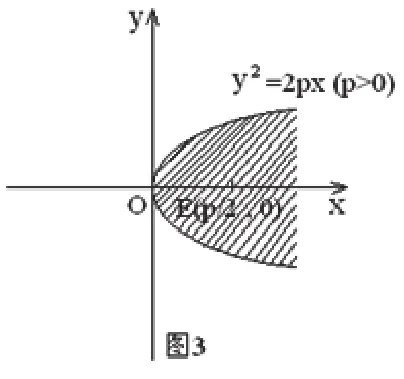
方程x2+y2=1表示以原点为圆心，半径为1的单位圆，而不等式x2+y2≤1就表示以原点为圆心，半径为1的单位圆及其内部。如图2，它是一个封闭区域。再如，方程y2= 2 p x( p ＞0)表示以坐标原点为顶点，焦点为E0），开口向右的抛物线。而不等式y2≤ 2 p x( p ＞0)则表示以坐标原点为顶点，为焦点，开口向右的抛物线及其内部。如图3，它也是一个开放区域。

总之一个区域总可以用一个图形把它准确地表示出来。

二、线性规划问题的解决

1.求区域面积

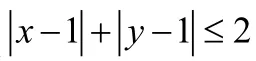
例1：求不等式表示的平面区域的面积

解：可化为

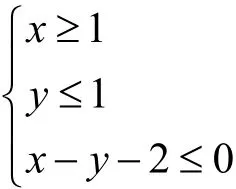
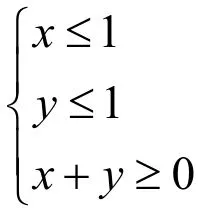
平面区域ABCD是边长为的正方形，因此所求平面区域的面积为8。

2.最值问题

所围成的区域内的不同两点，则

的取值范围是（ ）

A.(0 , 2]

B ( 0,

C ( 0,

解：作出可行域 如图5

顶点

A (1 , 2)B (1,1)C(5,1)

的取值范围是故选C

3.相关区域型问题的解决

例3：已知a, b ∈ R+，且方 程x2+ 2 a x + b =0与 方 程x2+ 2 b x + a =0都有实根，则

a+b 最小值为 。

分析：由已知，要想写出关于a+b 的代数式显然办不到，由已知可得到关于a,b的不等式关系，(2 a )2−4b ≥0且(2 b ( )2

a−, b

4 ) a ≥0,即

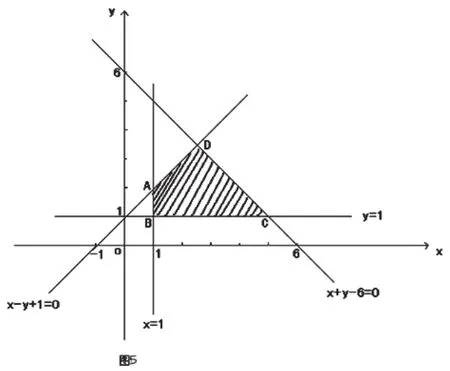
a2≥b 且b2≥a ，若把 看作一个动点坐标，考虑到a, b ∈ R+，则上述两式所表示的是两个区域，分别如图6与图7，而它们的公共部分如图8所示。

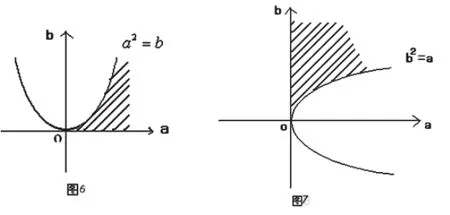
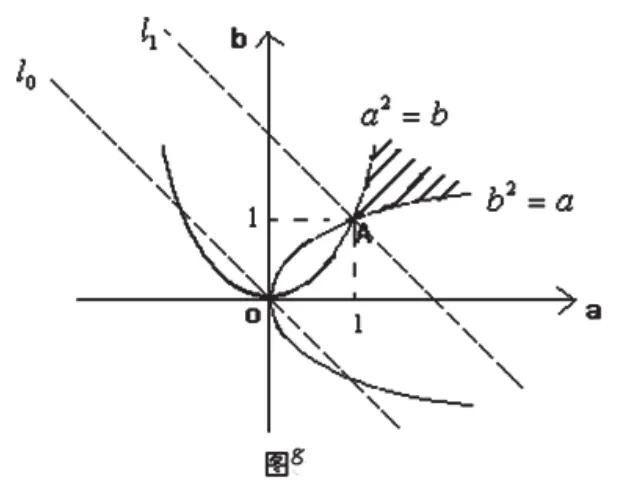
令z=a+b ，则b=−a+z

作直线l0： b=−a 并平移至l1过点A (1,1)，此时，zmin=1+ 1 = 2即a+b 的最小值为2。

由以上例题可见，线性规划问题的解决是用图解法，而与之相关的区域型问题的解决也是借助于图像解题，是典型的数形结合思想的应用。区域型问题的解决体现了数形之间的相互渗透，融合，这种解法把抽象思维和形象思维结合在一起，化解问题难度，使解题更灵活准确，科学化。此类题型的解决可培养学生的思维品质和数学素质，提高学生创造性运用数学基础知识的能力。