T3 晶格中无质量Dirac粒子的磁电约束和波导
程衍富,焦奎嵩
(中南民族大学 电子信息工程学院, 武汉 430074)
T3晶格中无质量Dirac粒子的磁电约束和波导
程衍富,焦奎嵩
(中南民族大学 电子信息工程学院, 武汉 430074)
从理论上研究了T3晶格中的载流子在非均匀磁场和电场构成的磁电势阱中的约束.利用磁电组合势阱中电势可调的特点,靠增加电势阱深度从而增加粒子的束缚态数,或者增加势阱区域的宽度来改变束缚态数.利用磁电势阱构成电子波导或者量子线,计算了波导的本征模和概率流密度,指出了T3晶格的磁电波导可成为有希望的纳米电子器件.
T3晶格;磁电约束;束缚态;波导
石墨烯的发现极大地引起了人们对二维材料的研究兴趣[1,2],因为在单原子厚的石墨烯层中载流子能量服从线性色散关系,它的行为像无质量Dirac费米子.在这个系统中可观察到许多不寻常的现象,例如手性载流子[3],反常Landau能级[4], 反常量子霍尔效应[5]和势垒中的Klein隧穿[6]等.除了石墨烯外,还有不少二维材料的载流子也满足相对论无质量Dirac方程.例如dice晶格,也称为T3晶格.实验表明这种晶格能在 SrTiO3/SrIrO3/SrTiO3三层异质结构中实现[7].另外利用光学手段也能产生dice晶格,即T3光学晶格中的冷原子的行为也可看成准相对论无质量Dirac费米子[8]. 不过在T3晶格中载流子的赝自旋S=1, 而不像石墨烯晶格中的赝自旋S=1/2. 由于T3晶格中载流子具有无质量Dirac费米子行为,因此和石墨烯一样也具有许多奇异性质.
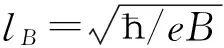
石墨烯中载流子的约束和波导已经被广泛研究,但在具有相同性质的T3晶格中载流子的约束以及由此构成的波导的研究还没有出现,为此,本文研究T3晶格中无质量载流子的磁电约束和波导.
1 磁电势垒对载流子的约束
在石墨烯中磁场能约束Dirac费米子,不过产生磁势垒需要沉积磁性材料在样品上,因此其参数很难随时改变,但磁电组合势垒则改变了这种状况[18].在T3晶格中由于平坦能带的存在[19],准粒子通过磁势垒展现与石墨烯中不同的行为[20],准粒子通过磁矢势的传输也具有与石墨烯不一样的特征[21].磁电组合也能改善准粒子传输,对构成以T3晶格为基础的纳米器件起重要作用.
考虑在 (x, y)平面上的T3晶格薄片上面放置紧挨着的绝缘层及长磁条带,磁化方向与晶格平面平行,并连接电栅极U.长磁条带产生局部高磁场,其不均匀磁场沿y轴不变而沿x轴为δ函数:
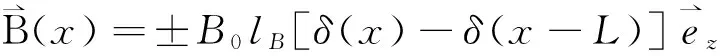
(1)
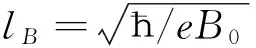
Ay(x)=±B0lB[θ(x)-θ(x-L)],
(2)
在长磁条带上放置电栅极,产生矩形电势为:
U(x)=±U0θ(x)θ(x-L),
(3)
其中θ(x)是Heaviside阶梯函数,U0是常数电势垒的高度.实验装置和势函数如图1所示.
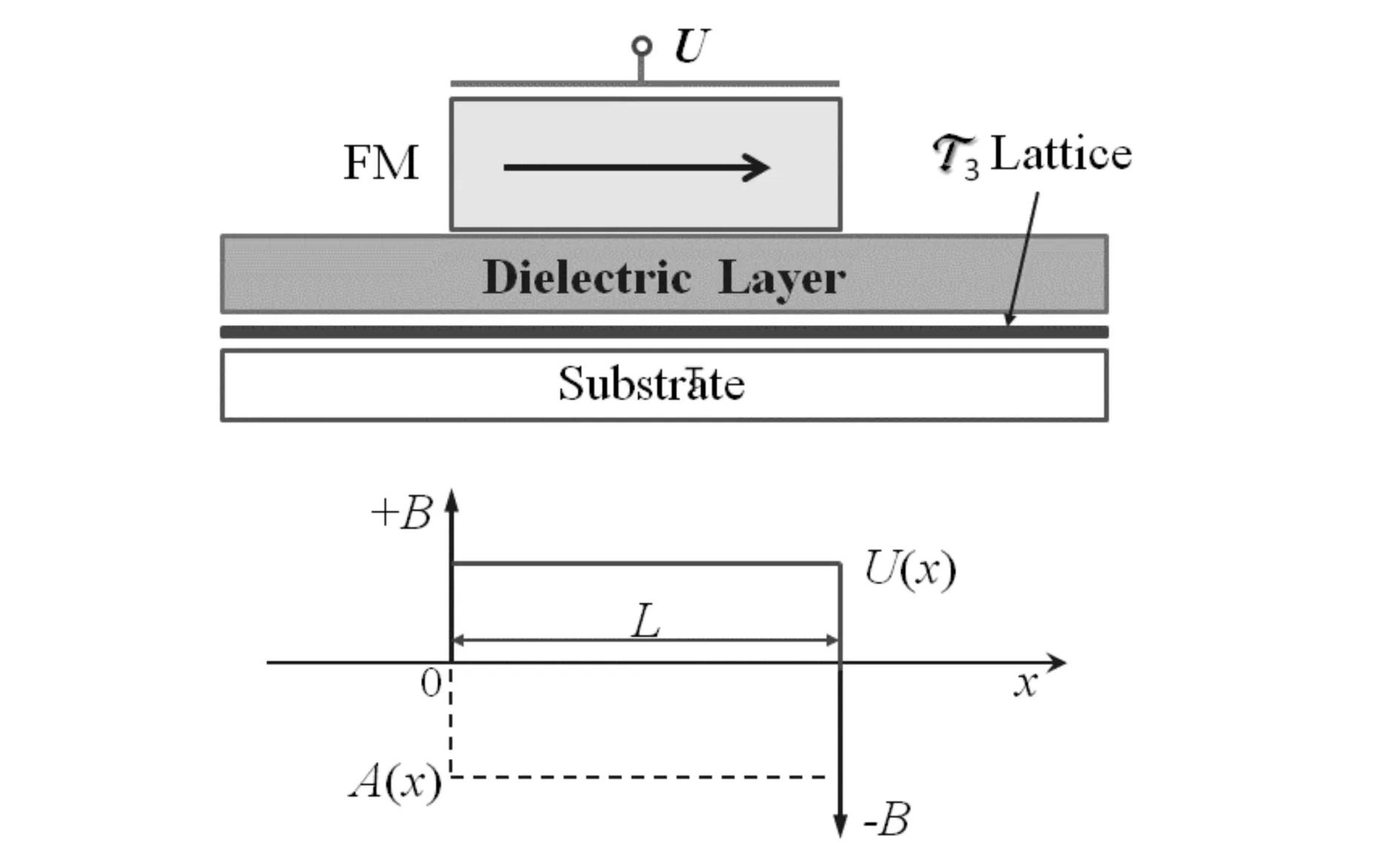
图1 实验装置示意图和磁电势阱Fig.1 Schematic of experimental setup and potential well profile
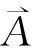
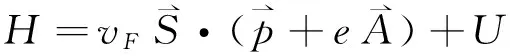
(4)
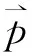
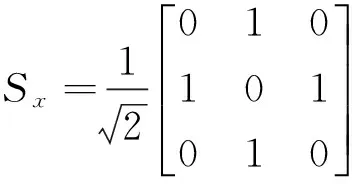
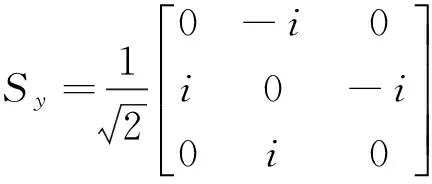
(5)
对给定系统,我们知道势函数与y无关,则准粒子在y方向动量py不变.粒子哈密顿量本征方程的波函数能写为如下三分量形式:
Ψ(x,y)=[ΨA(x),ΨH(x),ΨB(x)]Teikyy,
(6)
其中T表示矩阵转置,即列矩阵由T3晶格的三个子格表示的振幅组成.
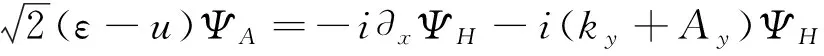
i∂xΨB-i(ky+Ay)ΨB,
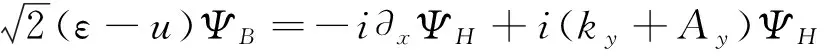
(7)
因此势垒区域Ay=±1,u=u0=U0lB/ħvF,无势垒区域Ay=u=0.
当粒子通过势垒界面,且不存在短波散射过程时,则可以忽略两能谷K和K′ 之间的散射[8]. 严格地讲势垒界面应该光滑变化,但当粒子的费米波长λF=2πħvF/|E| 远大于势垒变化范围,而势垒变化范围也远大于晶格常数,则在散射问题中可把势垒光滑变化当成阶梯势来处理[22].粒子波函数在界面两边要满足连续条件[20]:
ΨH(w)=ΨH(w),
ΨA(w)+ΨB(w)=ΨA(-w)+ΨB(-w).
(8)
这里w是沿x方向的小值.在完成波函数匹配后,我们最后需要取w趋于零.
从方程(7)可得到ΨH满足下面的二阶微分方程:
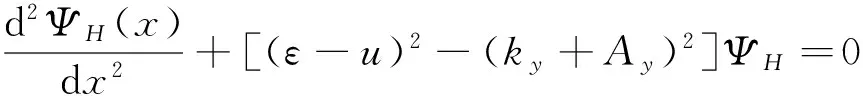
(9)
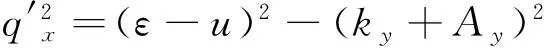
考虑势垒约束粒子,即在势垒区域形成行波,在势垒外面为衰减波,这相当于势垒变成势阱.在势垒区域取磁矢势阱Ay=-1,电势可调节为势垒或者势阱,即有下列条件:
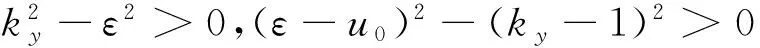
(10)
这里u0可正可负.如果不等式(10)的第二式不成立,则势垒区域出现沿x方向的衰减波,那么在某种条件下可能存在沿势垒界面y方向的行波,称为表面波[26]. 由于这种情况下准粒子的能量很小,因此本文不打算讨论.如果只考虑准粒子能量ε为正值,从不等式(10)知道,当u0<-1时,ky可取正负值;当u0>-1时,总有ky>0.我们只讨论ky>0 的情况,此时不等式(10)给出不同u0对应的ky和ε的取值范围,正如图2 阴影所示.在图2(a)和(b)中分别取u0=-1.5 和-0.5, 电势本身就构成势阱,再加上磁矢势阱,因此出现较大范围的束缚态区域.图2(c)对应u0=0,这里只有单独的磁矢势构成势阱,因此也出现束缚态区域.图2(d)对应u0=0.5,此时电势虽然为正值,但由于磁势阱的存在,因此仍然能出现束缚态.

图2 束缚态能量色散与ky的关系Fig.2 Energy dispersion of the bound states as a function of ky
正如以上分析,要在势垒区域出现束缚态,则势垒区域为行波而势垒两边为指数衰减波.因此方程(9)在不同区域的解为:
(11)
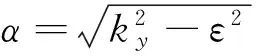
(12)
其中:
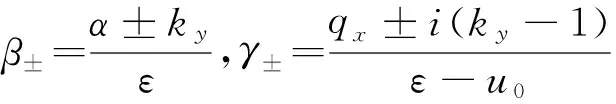
(13)
利用波函数在界面连续条件(8),可得到波函数振幅之间的关系:
(14)
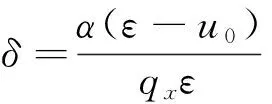
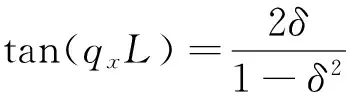
(15)
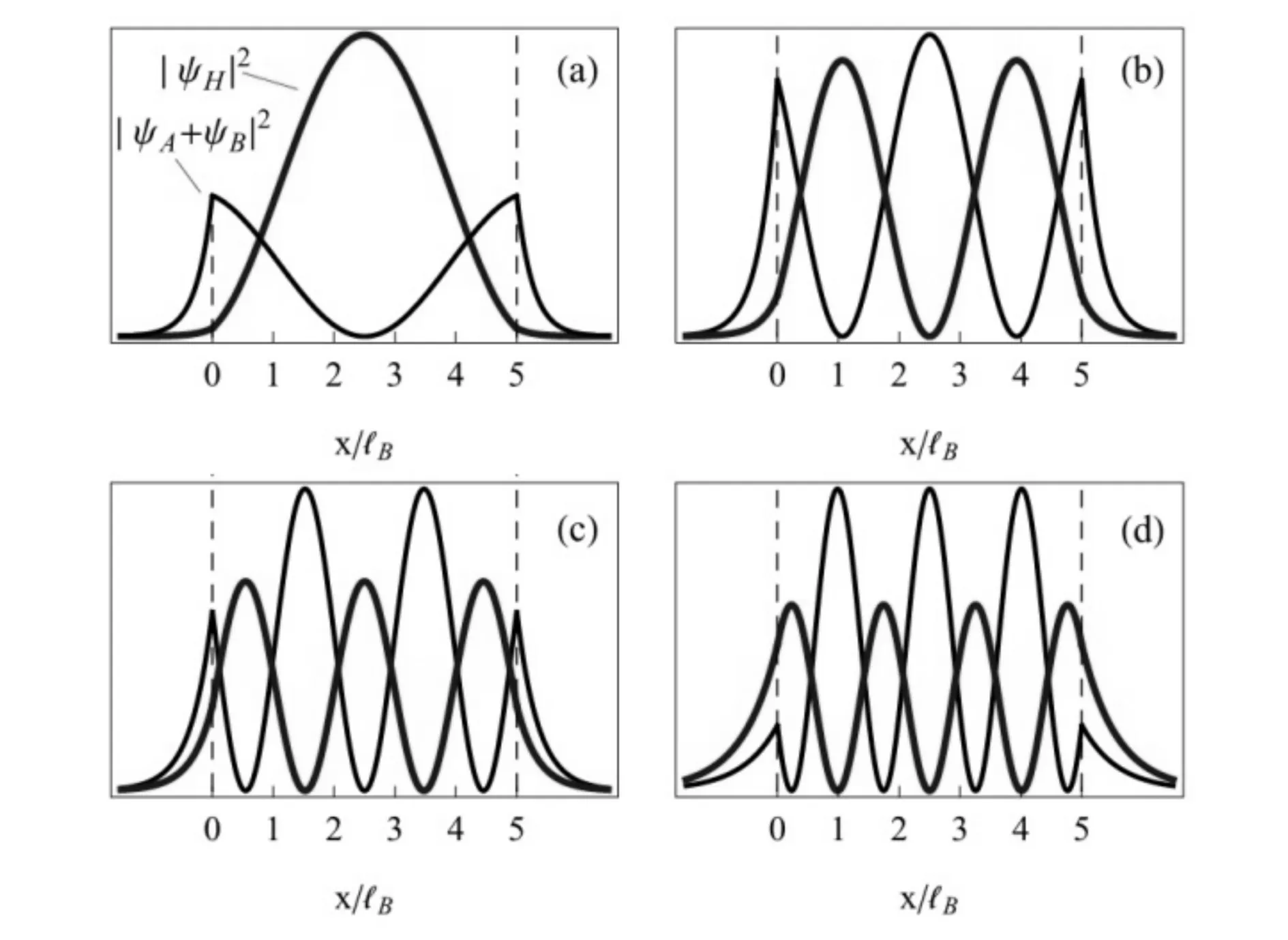
方程(15)给出了能量ε与波矢ky的关系,正如图2中的实线所示.这里无量纲参数磁矢势Ay=-1,电势分别取u0=-1.5(图2a),u0=-0.5 (图2b),u0= 0(图2c)和u0= 0.5(图2d), 而势阱宽度L=5.0.从图中可见,在相同的ky下, 电势阱愈深则出现的束缚数目愈多,u0为正值时也能出现束缚态, 这是由于磁矢势的作用.当势阱宽度L增加时, 相同区域束缚态数目也随之增加.图3(a)和(b)分别给出L=1.0和L=5.0 时的束缚态, 其中u0=-0.5.图3(c)和(d)给出对应的波函数本征模qx与ky的关系,当同时给定ky时就可给出束缚态数.例如在图3(b)和3(d)中标记点分别给出在ky=2.0的条件下能量色散方程(15)的数值解得到的4个束缚态或者本征模,其能量ε和qx分别为ε1=0.647,qx1=0.562(实心圆),ε2=0.985,qx2=1.098(三角形),ε3=1.394,qx3=1.609(正方块),ε4=1.807,qx4=2.079(空心圆).
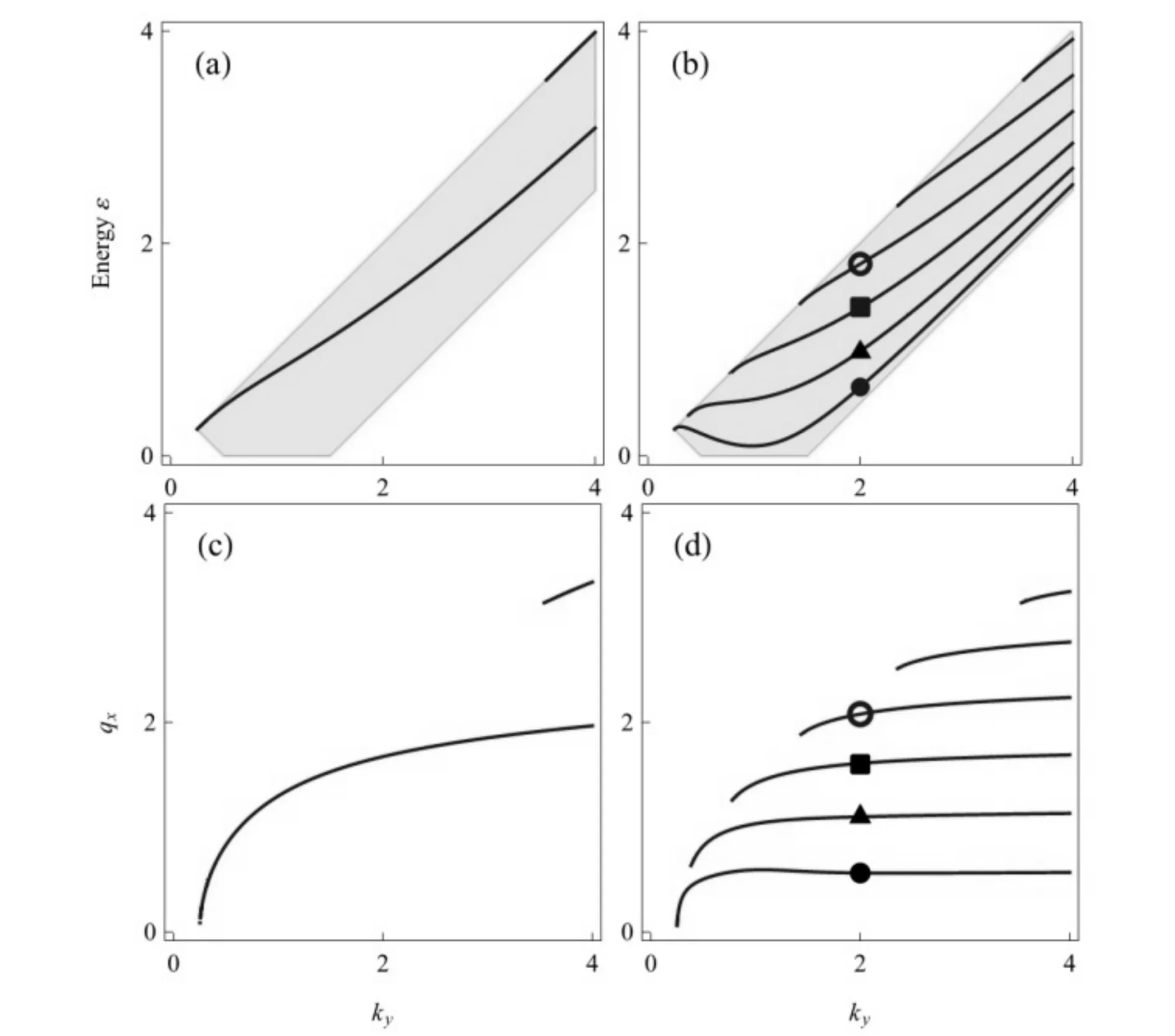
图3 束缚态能量与ky和波导本征模qx与kyFig.3 Spectrum of confined states vs kyand qxvs kyfor the eigenmodes
利用波函数归一化条件可求得归一化系数A为:
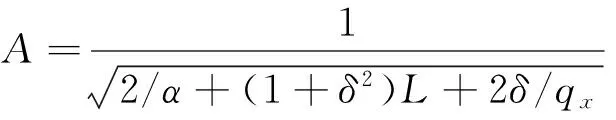
(16)
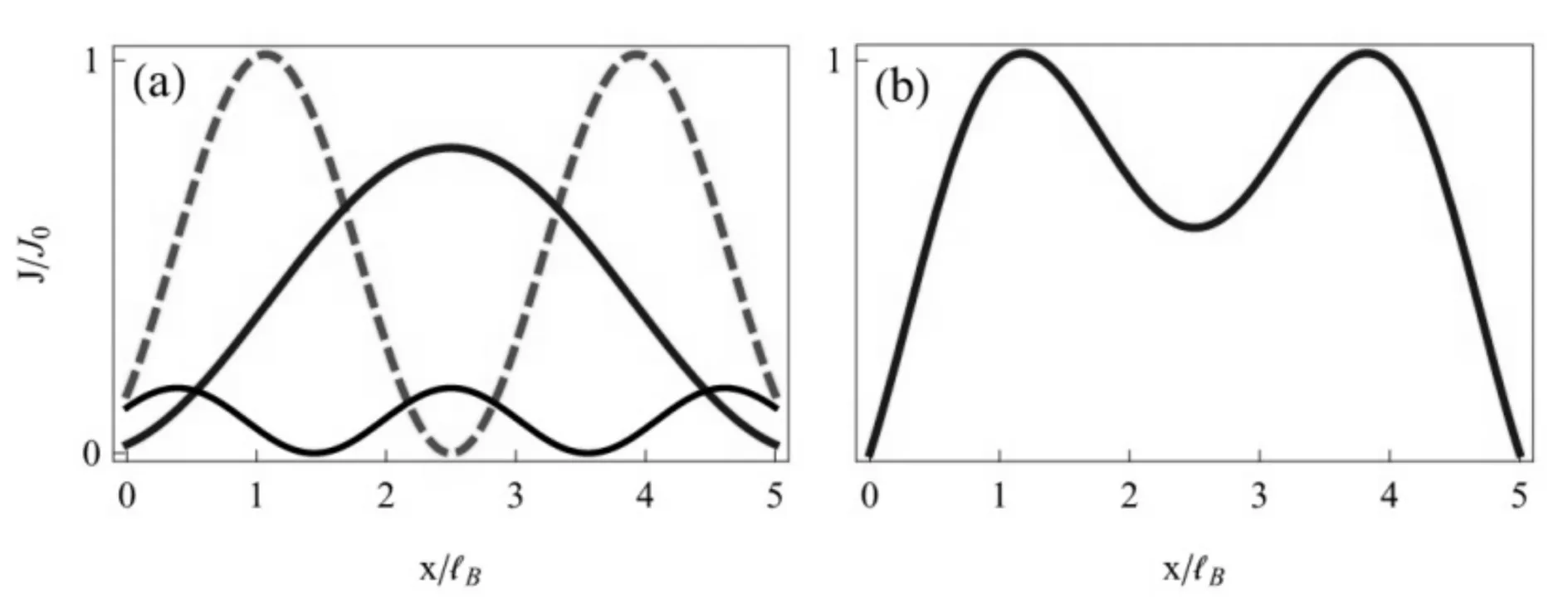
当nπ (17) 当nπ+π/2 (18) 由于波函数ΨH(x)和ΨA(x)+ΨB(x)在界面连续,因此我们也可得到δ取不同值时相应的概率密度|ΨH(x)|2和|ΨA(x)+ΨB(x)|2.图4给出L=5.0,u0=- 0.5,ky=2时的波函数概率密度分布,它们分别依次对应图3(d)中各标记点的波函数. 图4 束缚态波函数概率密度分布Fig.4 probability density of the wave function for the bound states 图4中|ΨH(x)|2用粗实线表示,而|ΨA(x)+ΨB(x)|2用细线表示.图4(a)和(c)中qxL/2分别为1.405和4.025,因此我们取δ=tan(qxL/2).而图4(b)和(d)中qxL/2分别为2.745和5.197,因此对应δ=-cot(qxL/2).由图4可知波函数在势阱区域为驻波,在势阱外面为衰减波,并且束缚态数等于概率密度的峰值数.图4中束缚态能量ε分别为0.647,0.985,1.394和1.807,其波函数概率密度峰值数分别为1, 2, 3和4个. 波导或者量子线,它使载流子在一个方向约束而在另一方向自由传播.在二维平面上构成波导有许多方法,比如化学方法,机械方法和电学方法[22].前两种方法虽然能约束粒子但都不方便调控,只有电学方法容易方便地调控载流子.对手性Dirac费米子,单纯的电势垒(如pnp结)总会出现Klein隧穿[23,24],单纯的磁势垒能构成波导但不利于调控[25],因此磁电组合势垒是构成可方便调控的量子线或者波导的最佳构型[22]. 图5 (a)电子波导示意图;(b)波矢,概率流密度和入射角θFig.5 (a) Schematic of electronic waveguide; (b) wave vector q, probability current density J and incident angle θ 在T3晶格用磁矢势阱和方便调节的电势垒构成波导,即势阱区域沿y方向很长而沿x方向很窄而形成量子线.准粒子在势垒区域不断的全反射而沿y方向传播,这正如普通光学纤维中的波导,图5(a)所示.入射粒子概率流密度J在界面不断反射形成波导区域的传导电流.确定能量ε的准粒子在波导内传播时,波矢q= (qx,ky)两分量的关系和入射粒子密度流J在图5(b)中.当ky确定后,可由圆心在(0,-Ay)半径为ρ=|ε-u0| 的圆确定波矢q的大小和方向,而入射粒子密度流J的方向决定入射角θ(图5), 它们满足如下关系: (19) 出现束缚态满足条件ky≥ε≥ky+Ay+u0,因此有: (20) 这里θc为出现反射的临界角.例如图3(d)中L=5.0,Ay=-1,u0=-0.5,ky=2时临界角为θc=23.58°. 图3(d)中各标记点对应的入射角分别为θ= 60.67°(实心圆),θ= 42.32°(蓝三角),θ=31.87°(正方块)和θ= 25.67°(空心圆). (21) 满足概率密度|Ψ|2=|ΨA|2+|ΨH|2+|ΨB|2的连续方程: (22) 由方程(21)计算得知在势阱区域束缚态的概率流密度分量Jx=0, 这是因为x方向没有粒子越过界面.当δ= tan(qxL/2) 时,其y分量为: (23) 当δ=-cot(qxL/2) 时有: (24) 其中J0=4vFħ.考虑准粒子能量ε=1,波导宽度L=5.0时的概率流密度在图6中,图6(a)中给出的3个本征模分量分别为qx1=0.56,ky1=2.39(粗实线),qx2=1.10,ky2=2.02(虚线)和qx3=1.49,ky3=1.19(细实线).图6(b)给出总概率流密度.从图6知道束缚态概率流密度完全分布在波导内,因此波导可作为传播准粒子的一维通道. 图6 波导中3个本征模的概率流密度Fig.6 The probability current density of the three eigenmodes in the waveguide T3晶格的低能能带结构为在Dirac点存在一个平坦能带和两个线性能带,这两个线性能带类似于石墨烯的低能结构,但赝自旋数为1而不是石墨烯的1/2.因此赝自旋矩阵是3×3矩阵,准粒子波函数有3个分量.研究了T3晶格中非均匀磁场形成的磁矢势阱和电势垒对准粒子的约束和由此构成的电子波导.在平行于y方向不变的磁矢势阱和电势下,导出了束缚态波函数以及束缚态粒子的能量色散关系.在势阱区域束缚态和准粒子的能量与势阱宽度L和电势u有关,增加电势阱深度可增加束缚态数,增加势阱宽度也可增加束缚态数.如此势阱可构成电子波导,给出了波导内入射粒子流的全反射临界角和相应的概率流密度.因此和石墨烯一样,T3晶格也有希望成为二维纳米器件的新材料. [1] Novoselov K S, Geim A K, Morozov S V, et al. Two-dimensinol gas of massless Dirac fermions in graphene [J]. Nature, 2005, 438: 197. [2] Castro Neto A H, Guinea F, Peres N M R, et al. The electronic properties of graphene[J]. Rev Mod Phys, 2009, 81: 109. [3] Goerbit M O. Electronic properties of graphene in a strong magnetic field [J]. Rev Mod Phys, 2011, 83: 1193. [4] Li G H, Andrer E Y. Observation of Landau levels of Dirac fermions in graphite [J]. Nat Phys, 2007, 3:623. [5] Zhang Y B, Tan Y W, Stormer H L, et al. Experiment observation of the quantum Hall effect and Berry′s phase in graphene [J]. Nature, 2005, 438: 201. [6] Katsnelson M I, Novoselov K S, Geim A K. Chiral tunneling and the Klein paradox in graphene [J]. Nat Phys, 2006, 2: 620. [7] Wang F, Ran Y. Nearly flat band with Chern number C=2 on the dice lattice [J]. Phys Rev B, 2011, 84: 241103. [8] Bercioux D, Urban D F, Grabert H, et al. Massless Dirac-Weyl fermions in aT3optical lattice [J]. Phys Rev A, 2009, 80: 063603. [9] Peres N M R, Castro Neto A H, Guinea F. Dirac fermion confinement in graphene [J]. Phys Rev B,2006, 73: 241403(R). [10] Martino A De, Dell′Anna L, Egger R. Magnetic confinement of massless Dirac fermions in graphene [J]. Phys Rev Lett, 2007, 98: 066802. [11] Myoung N, Ihm G. Tunneling of Dirac fermions through magnetic barriers in graphene [J]. Physica E, 2009, 42: 70. [12] Bliokh Y P, Freilikher V, Nori F. Tunable electronic transport and unidirectional quantum wires in graphene subjected to electric and magnetic fields [J], Phys Rev B,2010, 81: 075410. [13] Ghosh S, Sharma M. Electron transport and Goos-H?nchen shift in graphene with electric and magnetic barriers: optical analogy and band structure [J]. J Phys: Condens Matter, 2009, 21: 292204. [14] You J K, Zhang Lide, Ghosh P K. Electronic transport in nanostructures consisting of magnetic barriers [J]. Phys Rev B, 1995, 52: 17243. [15] Krakovsky A. Electronic band structure in a periodic magnetic field [J]. Phys Rev B, 1996, 53: 8469. [16] Bilokh Y P, Freilikher V, Savel′ev S, et al. Transport and localization in periodic and disordered graphene superlattices [J]. Phys Rev B, 2009, 79: 075123. [17] Agrawal N, Ghosh S, Sharma M. Electron optics with Dirac fermions: electron transport in monolayer and bilayer graphene through magnetic barrier and their superlattices[J]. International Journal of Modern Physics B, 2013, 27: 1341003. [18] Hartmann R R, Robinson N J, Portnoi M E. Smooth electron waveguides in graphene [J]. Phys Rev B, 2010, 81:245431. [19] Häusler W. Flat-band conductivity properties at long-range Coulomb interactions [J]. Phys Rev B, 2015, 91: 041102(R). [20] Urban D F, Bercioux D, Wimmer M , et al. Barrier transmission of Dirac-like pseudospin-one particles [J]. Phys Rev B, 2011, 84: 115136. [21] Cheng Y F, Jiao K S, Pan L F, et al. Magnetic barrier transmission of Dirac-like particles in aT3lattice [J]. Phys Scr, 2014, 89: 075803. [22] Rozhkova A V, Giavaras G, Bliokh Y P, et al. Electronic properties mesoscopic graphene structures: Charge confinement and control of spin and charge transport [J]. Phys Rep, 2011, 503: 77-114. [23] 焦奎嵩,曹振洲,程衍富. 无质量手性狄拉克费米子的克莱恩隧穿[J].大学物理,2014,33(20):10-13. [24] 潘林峰,曹振洲,程衍富.有质量手性费米子的势垒隧穿[J].中南民族大学学报:自然科学版,2014,33(3):65-69. [25] Myoung N, Ihm G, Lee S J. Magnetically induced waveguide in graphene [J]. Phys Rev B, 2011, 83: 113407. Magnetoelectric Confinement and Waveguide of Massless Dirac Particles in aT3Lattice ChengYanfu,JiaoKuisong (College of Electronic and Information Engineering,South-Central University for Nationalities,Wuhan 430074,China) The confinement of Dirac particles have been investigated theoretically where potential well with electric and inhomogeneous magnetic fields is perpendicularly to theT3lattice plane. It has showed that the bound states number can be tuned by the potential well which dependence on depth and width of the potential well. The electronic waveguide or quantum wire can be formed by magnetic and electric potential well. The eigenmods and probability current densities are calculated in theT3lattice waveguide. We hope that these characteristics can provide potential applications in the nano-material waveguide devices. T3lattice; magnetorelectric confinement; bound states; waveguide 2015-06-29 程衍富(1956-),男,教授,研究方向:低维系统量子输运,E-mail:chengyf@mail.scuec.edu.cn 国家自然科学基金资助项目(11204383) O469.1 A 1672-4321(2015)03-0058-06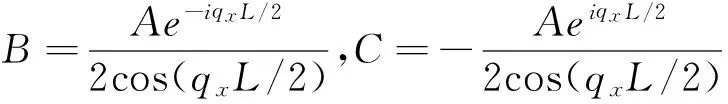
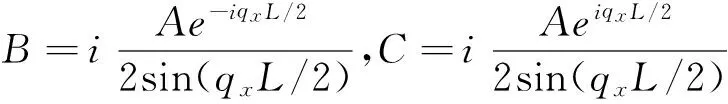
2 磁电势垒构成波导

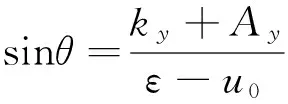

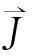
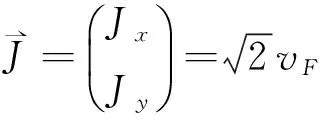

3 结语

