半开放系统中的粒子逃逸问题*

张茂芳 游慧敏 尹相国 张云波

1)(山西大学理论物理研究所,量子光学与光量子器件国家重点实验室,太原 030006)

2)(浙江理工大学物理系,浙江省光场调控重点实验室,杭州 310018)

研究了半开放系统中粒子向开放空间的隧穿问题.考虑由无限高的墙和多个 δ 函数势垒组成的半Dirac 梳模型,首先求解该模型的精确解析解,其能量本征函数可以用递推关系以封闭解析的形式给出.对单个势垒、多个势垒、无序势垒等不同情况,利用傅里叶积分计算了任意时刻单粒子波函数的明确表示,导出了由初态保真度定义的粒子生存几率闭合形式的表达式,重点研究了粒子生存几率对势垒高度、无序强度等系统参数的依赖,以及利用相关参数对衰减规律的操控及抑制.发现多个势垒将大幅度提高粒子的生存几率,无序的加入会极大地抑制其随时间的振荡.

1 引言

粒子从势阱隧穿到空间是量子力学的基本问题之一,已被用于分析诸如核α衰变[1,2]、质子发射[3,4]、聚变[5]、裂变[6]、光缔合[7]、光解离[8]、或隧道二极管的功能[9]等现象.多年来,人们已经详细研究了粒子隧穿进入开放空间的许多方面.如单粒子隧穿过程和多体玻色-爱因斯坦凝聚体的隧穿现在已经得到了很好的解释[10-16].近年来,由于超冷原子物理领域实验技术的快速发展,可以设计出特色新颖的隧穿系统,如改变外势的形状[17-19]、有效维度[20-23]、制备初态[24]、或调节粒子间相互作用的强度[25,26].这一领域最近的重要实验成果包括海德堡的塞利姆·约希姆小组的实验,他们研究了隧穿少费米子系统的衰变[27,28].

本文考虑的则是半开放系统,可以看作是Winter 模型[29]的一个推广.Winter 模型由一个无限高的墙和一个δ函数势组成,它的一个很好的特点是其能量本征函数可以以封闭解析的形式找到,使我们能够很容易地洞察衰变粒子的性质.温特指出衰变过程与指数律存在偏差,其长期演化遵循幂律.研究表明根据任意初始受限状态的完整共振谱可导出生存几率和非逃逸概率,它们在很长一段时间内遵循不同的幂律衰减[30],在各种实验中也观察到非指数衰减[31—33].实验技术的新进展提供了以可控方式研究隧穿现象的机会[24,27],有助于更好地理解不稳定多体状态的特性.如最近的研究包括两个相同的非相互作用粒子系统[34]、超冷原子系统[35-42]、具有库仑相互作用的两粒子系统[43]、以及由一个核-核和两个价质子组成的模型系统[44].双势垒情况下的Winter 模型已经得到了很好的应用,特别是最近关于不稳定Tonks-Girardeau 气体从中逸出的研究[45]带给我们很多启发.

本文将Winter 模型进行推广,初始位于宽度为a的无限深势阱中的粒子,右势垒突然撤掉后向开放空间隧穿,右方N个势垒与原来的无穷高左势垒组成的系统我们称之为半Dirac 梳模型，如图1所示.本文首先求解该模型的精确解析解,考虑其含时演化,利用生存几率来分析粒子的逃逸情形,讨论其衰减特性,以及加入无序后对隧穿过程的影响.

图1 半开放系统中的粒子逃逸问题.初始位于宽度为a 的无限深势阱中的粒子,右势垒突然撤掉后向开放空间隧穿,右方N 个势垒与原来的系统组成了半Dirac 梳.图中显示了初始时刻及 t=10t0 时在各阱的几率密度分布.这里取N=10Fig.1.Particle escape problems from a semi-open system.A particle initially in the eigenstate of an infinite potential well of width a is released at t=0 and tunnels into open space when the right barrier is suddenly switched off,and the N δ-barrier on the right form a semi-Dirac comb with the original well.The probability density is shown fort=0 and 1 0t0 .

2 模型

考虑一个 (0,∞)的一维系统,其中有N个均匀分布的δ势垒:

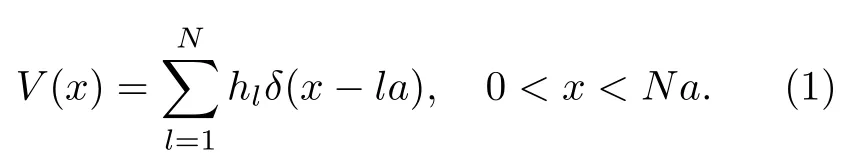
势垒强度hl≥0,a为势垒间隔.在此之外,外势为零,x＞Na时V(x)0 .最初,粒子被限制在(0,a)的势阱之间,假定初态为由n1,2,3,···标记的基态或激发态:

这里展开系数Cn(p)由初始波函数确定:

可以证明这个积分是收敛的,并且得到的波函数对于给定的边界条件是平方可积的,也即它属于相关的希尔伯特空间.

为了得到Ψ(x,t)的解,首先需要求解哈密顿量H由p标记的连续谱本征态ϕp,其定态方程为

这里′表示空间一阶导数.在不同的区域系统波函数设为如下统一的形式:

其中l0,1,2,···N-1,注意该式对x＞Na区域也成立.由边界条件可以得到系数Al,Bl满足的递推关系如下:

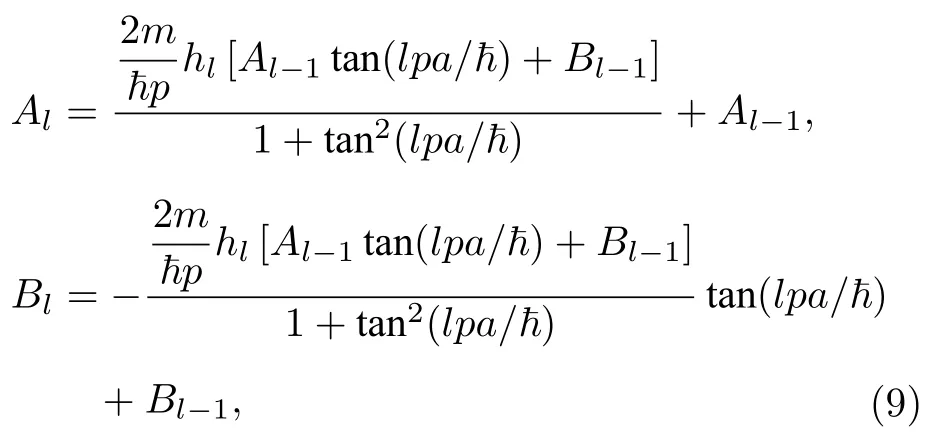
其中因波函数在x0 处为0,所以有A01及B00.由此得到系数A1和B1,A2和B2,···,最终得到AN和BN.本征函数ϕp在如下内积定义下是正交、归一、完备的:

因其本征值为连续谱,正交归一关系为δ函数归一化:

这里采用的狄拉克δ函数的极限表达式为

由此可得(8)式中的归一化系数D为

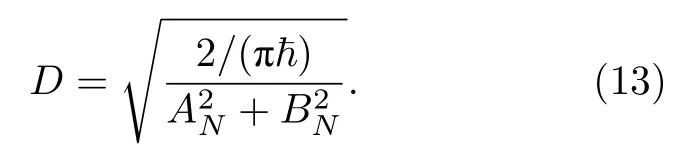
之后将波函数ϕp代入(4)式中的积分,可得到Cn(p)的解析表达式:

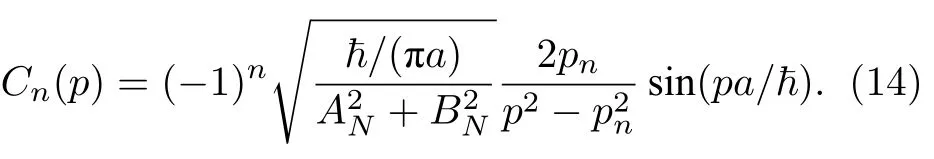
根据生存几率(也称量子保真度)来分析系统的衰变特性:

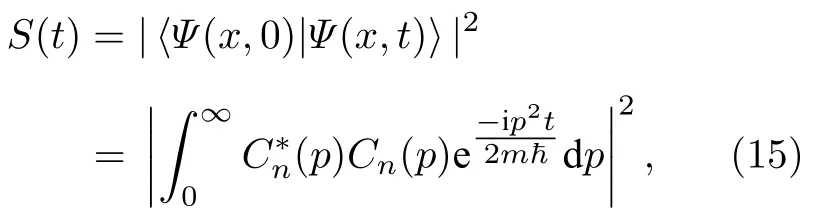
这是时间演化状态保持其初始状态的概率,以此来衡量二者之间的差异.

为了方便快捷地求解S(t),在数值上可以用傅里叶变换计算(15)式积分.为此令ωp2/(2mℏ),则 dω/dpp/(mℏ),可以得到

其中F(t)是f(ω)的傅里叶变换,即

这里

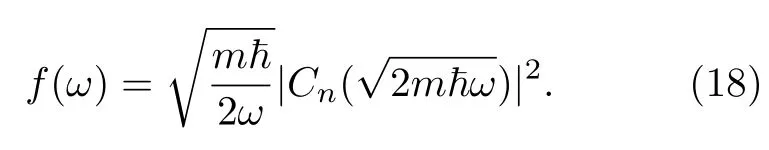
本文选择空间坐标和时间坐标单位分别为a0a和t0ma2/ℏ,势垒强度以h0ℏ2/(ma)为单位.注意这里的势垒强度的量纲是: 能量·长度,它与δ函数中提出的 长度-1量纲一起贡献势能.

3 结果分析

3.1 单个势垒

首先讨论单个势垒的情形,此时系数

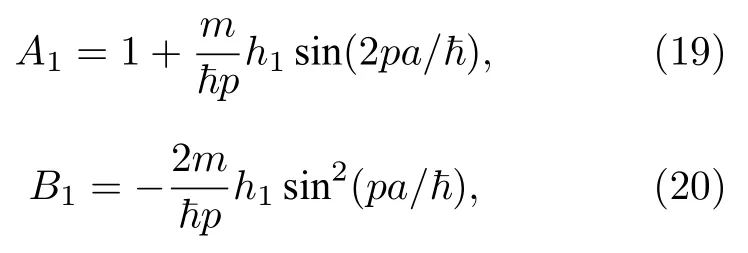
表明势垒强度hh1完全决定了系统的隧穿性质.为方便起见,在以下的分析中考察生存几率的对数函数随时间的变化规律.对S(t)取对数,直线部分表示指数衰减,在某个时间段TT2-T1内的衰减快慢可以用其斜率k来描述

首先考虑单个势垒时固定势垒强度,生存几率随初始能量的变化情况.图2 给出了势垒强度h10h0,粒子处于最低的5 个初态能级(n1,2,3,4,5)情况下的隧穿动力学.粒子的衰减情况可分为三个阶段,指数衰减伴随着剧烈振荡: 在开始时的第一阶段,短时t0-30t0情况,高能成分迅速逃逸,生存几率在短时内指数衰减,n越高的初态生存几率到达振荡点的时间越短,l nS的斜率k随着能级n的增加逐渐增大,说明粒子的衰减速率随初始能量的增大而加快;中间时段t20-140t0时,随着状态的演化,高能成分被耗尽,粒子的平均能量接近能谱中的最低能量,粒子仍然保持指数衰减的趋势,但衰减速率减慢,所有初始能级的斜率k趋于一致;长时t300t0-∞时,粒子衰减逐渐趋于稳定,生存几率降低到某个平衡值便不再变化,这个值 l nS∞随能级n的增大而减小.图2的小图分别给出了衰减速度及平衡值随初始能级的变化趋势.

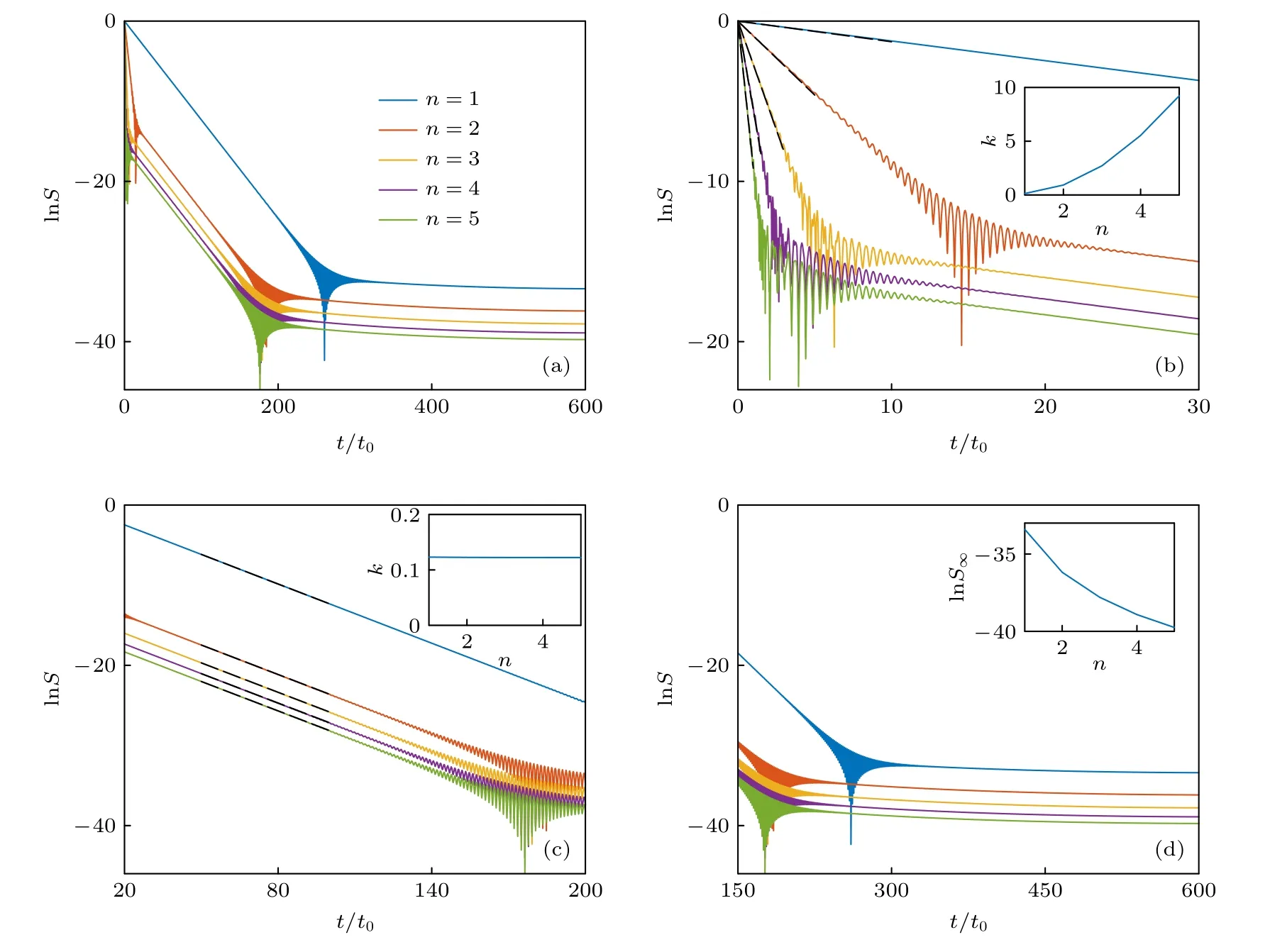
图2 (a)单个强度为 h=10h0 的势垒,能量最低的5 个初始态的生存几率(n 表示初态时粒子所处的能级);(b)短时情况,黑色虚线处粒子的衰减率随着能级增高而增大;(c)中间时刻,黑色虚线部分粒子的衰减率不随能级而变化;(d)长时情况,粒子生存几率最后趋于的平衡值(l n S∞),随着能级增高而减小Fig.2.(a)The survival probability of the five initial states with the lowest energy for single barrier (N=1)with strength h=10h0;(b)the decay rate of the particle (black dotted lines)in short-term becomes faster for higher energy level;(c)in the medium-term,the decay rate of the particle (black dotted lines)does not change with n;(d)the equilibrium value (l n S∞)of the survival probability after the long-term decay decreases as the energy level increases.

然后考虑单个势垒时粒子处于基态,生存几率随势垒强度变化的情况.图3 给出了势垒强度分别为h(10,20,30,40)h0,基态n1 时粒子的生存几率随时间演化的情形.四个图分别给出了不同时间段下粒子的衰减情况,可分为两个阶段: 短时t0-30t0中,粒子呈指数衰减,势垒强度大时粒子会更多地困在阱中,l nS的斜率k随着势垒强度h的增大逐渐减小,说明粒子的衰减速率随势垒强度的增大而减慢;中间时段t300t0-3000t0时,粒子保持指数衰减的趋势,随着h的增加,生存几率到达振荡点的时间越来越长,粒子的衰减速率与短时内保持一致;长时t6000t0-∞时,粒子衰减逐渐趋于稳定,生存几率降低到某个平衡值便不再变化,这个值(l nS∞)随势垒强度h的增大而减小.图3 中的小图分别给出了衰减速度及平衡值随势垒强度的变化趋势.

图3 (a)单个强度为 h=(10,20,30,40)h0 的势垒初始基态的生存几率(n=1);(b)短时情况,黑色虚线处粒子的衰减率随着势垒强度的增大而减小;(c)中间时刻,粒子保持短时内的衰减率;(d)长时情况,粒子生存几率最后趋于的平衡值随着势垒强度的增大而减小Fig.3.(a)The survival probability of the initial ground state (n=1 )when N=1 and the barrier strengthsh=(10,20,30,40)h0;(b)the decay rate of the particle (black dotted lines)in the short-term decreases with the increase of the barrier strength;(c)particle maintains a short-term decay rate in the medium-term;(d)the equilibrium value of the particle survival probability after the long-term decay decreases with the increase of the barrier strength.

从以上单个势垒的隧穿情况来看,不同衰减时间范围内,粒子生存几率的衰减服从不同趋势.所有处于基态或激发态的粒子的生存几率在短时间内按S～e-Γ t的形式指数衰减.在一段时间后,激发态的衰变会以与基态相同的衰变常数进行.最终S(t)的衰减遵循一个长时间的反幂律.在不同的衰减时间区间曲线会有突变,并伴随着明显的振荡,这些过渡区域的振荡是由指数率和反幂律项的干涉导致的,而长时非指数衰减则是由于系统能谱具有下限[46].增加势垒强度h会极大地增加粒子留在阱中的几率.我们期待增加势垒个数也会达到同样的效果,以下讨论多个势垒对粒子隧穿特性的影响.

3.2 多个势垒

首先讨论势垒强度相同的多个势垒情况.更具体的来说考虑初始处于基态的粒子向势垒强度都为h的N10 个势垒组成的右半空间的逃逸问题.图4 给出了势垒强度分别为h(5,15,50)h0时,基态能级n1 粒子的生存几率随时间演化的情形,四个图分别展示了不同时间段下粒子的衰减情况.可以看出势垒强度较小(h5h0)时,粒子仍然指数衰减,随着强度增大,生存几率迅速升高并开始随时间不规则地振荡,并且在很长时间内保持,振荡幅度随h的增大也迅速增大.我们看到短时t0-120t0中,三种势垒强度情况下粒子的生存几率分别在t ≈(20,40,110)t0左右开始振荡,开始振荡时间随势垒强度增加.我们发现这种振荡可以在某个时刻将生存几率恢复到相当高的值,图4中间时刻t300t0-600t0,黑色箭头标记出了h50h0时粒子生存几率的振荡最高点,此时其对应的时间为tmax394t0,l nSmax值为-0.8543,意味着生存几率达到了初始态的 4 2.56%;长时t4800t0-6000t0时,生存几率持续在高位振荡,在某些时刻仍然可以达到非常高的量子保真度.

图4 (a)势垒数目 N=10,势垒强度 h=(5,15,50)h0 时能量最低的初始基态的生存几率;(b)-(d)分别为短时、中时、长时的行为.(c)图黑色圆圈处为 h=50h0 时粒子生存几率的振荡最高点Fig.4.(a)The survival probability of the initial state with the lowest energy for N=10 identical barriers for three barrier strengths h=(5,15,50)h0;(b)-(d)are short-term,medium-term,long-term behavior,respectively.The black circle in panel (c)indicates the highest point of oscillation of the survival probability for h=50h0 .

多个势垒时粒子在势垒间反射透射相互干涉,对较大的势垒强度,粒子发生反射的概率增大,隧穿出去的粒子可能被反弹回来,生存几率的振荡也越来越剧烈,并在某些时刻达到较高的保真度.从短时内可以看出粒子的衰减速率随着势垒强度的增大而变慢,到达发生振荡所需要的时间也更长.从长时来看,势垒强度增大到一定程度时,衰减速率基本保持稳定,非常缓慢衰减.可以找到振荡最高处的峰值,观察其随势垒数目的变化.

图5 给出了势垒强度分别为h(5,15,50)h0时,粒子生存几率的振荡最高点 l nSmax及其对应的时间tmax随势垒数目N变化的规律,每个点表示不同势垒数目所对应的值,线表示其拟合结果.可以看到粒子生存几率的振荡最高点 l nSmax随着势垒数目的增加而线性降低,随着势垒强度的增大而略微升高,但不同的势垒数目有较大的涨落.为了更清楚地理解生存几率最高点随势垒数目的变化,取h40h0情况下20 个振荡最高峰值的平均,可以看出粒子达到多个最高点的平均几率虽然总体降低,但更加表现出随势垒个数线性降低的趋势.而振荡最高点所对应的时间tmax随势垒数目的增加而呈现抛物线型增大,随着势垒强度的增大也逐渐变长,可以看到对某些势垒数目(如N14,18 等处)仍然会有最高点时间或迟或早出现的情形.

图5 势垒强度 h=(40,50,60)h0 时,粒子生存几率的振荡最高点(a)及其对应的时间(b)随势垒数目的变化.浅蓝色圆点对应 h=40 时不同势垒数目下粒子生存几率振荡多个最高点(此处取20 个)的平均值Fig.5.Variation of the peak value of the oscillation of survival probability (a)and its corresponding time (b)with the number of barriers for barrier strengths h=(40,50,60)h0.The light blue dots in (a)correspond to the average of 20 highest points in the oscillation for different numbers of potential barriers with strength h=40 .

随着势垒强度增大、数目增多,粒子的衰减速率逐渐减慢,在某些时刻生存几率长时间在高位振荡,甚至不再衰减.根据安德森局域化的理论,无序会导致波函数发生指数衰减,出现局域化现象.这里考虑引入无序势垒,势垒强度满足如下分布:

其中hmin为势垒最低强度,Δh为无序强度,R为[-1,1]范围内的随机数,即开放区间的势垒强度在(hmin+Δh)和(hmin-Δh)间随机分布.

图6 给出了不同势垒数目、不同势垒强度情况下引入无序后粒子的生存几率随时间演化的情形.首先选取较少势垒个数N10 时两种最小势垒强度分别为hmin10h0和4 0h0,无序强度分别为零Δh00,较小 Δh1,较大 Δh2情况进行比较.对hmin10h0,较小无序强度取作 Δh13h0,较大无序强度取作Δh29h0;而对hmin4 0h0,Δh15h0为较小,Δh235h0为较大.图6 中所有数据都是100 次无序势垒构型的平均.可以看到引入无序会极大地增加生存几率,而且随着无序强度的增大,粒子的生存几率增大,衰减速率减慢.hmin40h0时无序的引入会抹平没有无序时的剧烈振荡.另一方面,较多势垒个数N100 时,无论hmin取值大小,随着无序强度的增大,粒子生存几率的振荡都会被抹平,在hmin10h0情况下,抹平的保真度大大超过了没有无序系统的振荡最高点.

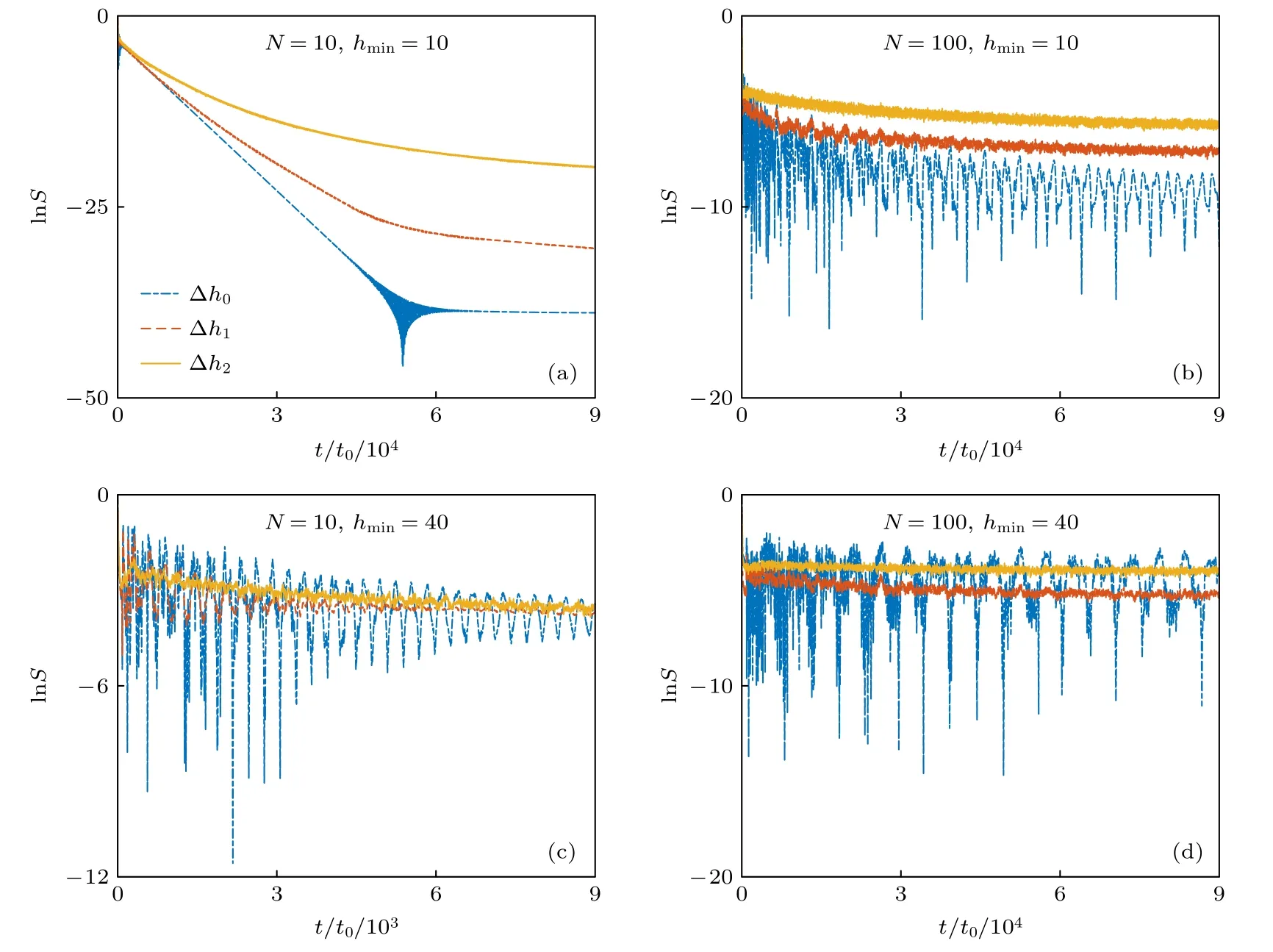
图6 N=10和N=100 个无序势垒组成的半开放系统中粒子的生存几率在大小两种无序强度下与没有无序(Δh0=0)情况的对比.图中所有数据都是100 次无序势垒构型的平均 (a),(b)hmin=10h0,Δh1=3h0,Δh2=9h0;(c),(d)hmin=40h0,Δh1=5h0,Δh2=35h0Fig.6.The survival probability of the particle for N=10 and N=100 barriers with randomly distributed strengths.Here Δh0=0denotes the case of regular barriers without disorder.All data in this figure are averaged over 100 disorder realizations of the barrier configuration.(a)(b)hmin=10h0,Δh1=3h0,Δh2=9h0;(c),(d)hmin=40,Δh1=5h0,Δh2=35h0 .

4 结论与展望

本文详细研究了半开放系统中的粒子的逃逸问题,即初始位于无限深势阱中的粒子右势垒突然撤掉后向开放空间隧穿,右方等间距分布的多个δ势垒组成了半Dirac 梳,重点研究系统初态的生存几率或量子保真度.解析得到了该系统的连续谱本征态,根据傅里叶积分计算了任意时刻单粒子波函数的精确解,导出了粒子一般情况下生存几率的闭合形式的表达式,利用其揭示了粒子逃逸过程的机制,分析了单个势垒和多个势垒时的衰减规律.发现对多个势垒,粒子生存几率可以达到 4 2.56% .引入无序势垒可以大幅提升生存几率,并极大地抑制其随时间的振荡.本文的研究将有助于理解粒子在无序系统中的衰变过程,并对利用势垒对系统进行相关的量子调控有指导作用.该研究同样适用于其他类型的势垒,比如有宽度的方形势垒,它在宽度b趋向0,高度V趋向无穷大的极限情况下等效于一个强度为V b的δ势垒,粒子在势阱中的逃逸问题可以类似求解.此种情况下可以单独考虑粒子逃逸随两个参数的依赖关系,我们期望得到和多个δ势垒的情况定性一致.此外,还可以利用均方位移[47,48]对时间的依赖σ2(t)～tγ来研究初始波包随时间的演化过程,除了均匀晶格中的弹道扩散 (γ2)和无序晶格中的局域化 (γ0)以外,在准周期晶格中可能存在超扩散 (1＜γ＜2)和亚扩散 (γ＞2)等现象,这些现象进一步丰富了粒子隧穿的动力学行为.