快速简单估计两因素交互作用

王玉枝，邢春峰

(北京联合大学基础部，北京 100101)

快速简单估计两因素交互作用

王玉枝，邢春峰

(北京联合大学基础部，北京 100101)

鉴于在试验设计中估计交互作用的繁杂性，提出一种快速简捷估计两因素交互作用的新方法。该方法应用过程简单、计算量小，具有很好的稳定性、可靠性及精确性。同时也分析了该方法适用于实际应用的特征，并用非线性二次回归模型说明原理。

试验设计；交互作用；非线性二次回归

交互作用作为试验设计中重要的辅助信息和手段，对建模和预测的估计精度有较大影响[1，2]。目前，交互作用的估计通常是利用完全组合设计和不完全组合的正交设计来实现[3，4]，计算量大，对数据的要求严格。之后出现使用回归分析方法来对非正交设计中的交互作用做近似估计[5]，回归分析方法利用回归模型反过来找缺失点的响应值，再运用完全组合设计计算交互作用，其计算量大，结果不精确。文献[5]中也对二水平因素的主效应和交互作用作了定义，在文献[6]中指出了该定义存在着一些问题。在试验设计中，因素间是不是存在交互作用、若存在是不是显著、在做试验设计时对交互作用如何处理，做到既省时间又省物力是广大科学工作者的难题。

本文提出在两因素试验设计中一种快速、简捷估计交互作用的新方法，其操作简单，易于编成程序，在计算机上执行，以下称为快简方法。该方法体现了在应用中交互作用随因素水平变化及水平组合变化而变化的特征，同时用非线性二次回归模型分析说明了该方法的原理，并用实例证实了该方法的稳定性、可靠性及精确性。

1 快简方法的使用过程

以估计任意两个因素A和B的交互作用大小为例，阐述快简方法的使用过程，如表1做4次试验，a1和a2为A的水平数，b1和b2为B的水平数，y为试验的响应值。

因素A取水平x1等于a1～a2之间的数值；因素B取水平x2等于b1～b2之间的数值时(x1≥0,x2≥0，且x1与x2的量能用数字表示)，响应值y在(x1,x2)点的交互作用的大小可以利用以下公式计算：

表1 快简方法的使用过程

(1)

则交互作用在该点的贡献率(交互作用在全部效应中所占的比例)为：

(2)

2 快简方法的原理

非线性回归分析法是数理统计中一种常见的分析方法，进行二次回归设计就可以满足一般的非线性问题的基本要求[7]，把A、B两因素试验中的各个主效应和交互作用及常数项表示成非线性二次回归模型：

按表1数据得4次试验的响应值为：

3 对快简方法的验证及结果分析

为进一步研究快简方法对交互作用计算的可靠性与准确性，用快简方法计算了显然有交互作用和无交互作用的非线性函数问题。

算例1y=cosx1+sinx2，做3次试验，计算交互项系数β12都为零。

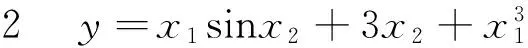
表2 实验数据

算例3[8]Goldstein and Price[9]，试验数据如表3。

f(x)=[1+(x1+x2+1)2(19-14x1+3x12-14x2+6x1x2+3x22]× [30+(2x1-3x2)2(18-32x1+12x12+48x2-36x1x2+27x22)]

表3 实验数据

从算例1的变量关系来看，显然没有交互项，没有交互作用，验证的结果与实际一致。算例2和算例3都做了3次试验，计算了12个点的交互作用贡献率，数据显示2个算例在不同的试验中相同和相近点的交互作用贡献率非常相近，说明快简方法具有很好的稳定性和可靠性。

在实际中，交互作用和各因素的水平及因素的水平组合条件有关。如果因素水平个数或因素水平所在范围发生变化，那么因素的交互作用也会跟着变化[6]。快简方法体现了因素间交互作用这一特征，每次试验的交互项系数的变化[9，10]，体现了这一变化及回归模型在不同点是变化的，但相同点在不同试验中交互作用的贡献率是稳定的，显示了快简方法的优势。

快简方法的交互作用的贡献率是交互作用的绝对值与全部主效应的代数和的绝对值加上交互作用绝对值之比，比用方差分析计算交互作用方法[4]中的平方和分解计算更为精确。

4 结 语

通过以上对快简方法的阐述、分析及验证，为估计两因素交互作用提供了一种新方法和思路。研究有待进一步深入，继续探讨多因素交互作用的估计及实物试验和误差的考虑将是以后努力的方向。

[1]Park K，Ahn J H.Design of experiment considering two-way interactions and its application to injection molding processes with numerical analysis[J].J Mater Process Tech.2004，(146)：221-227.

[2]王晓东，田俊.多因素交互作用及可信区间的估计[J].数学的实践与认识，2009，39(10)：122-126.

[3]张里千.交互作用和多因素最优化[J].数理统计与管理，1991，(03)：28-35.

[4]张里千.数学误用四例[J].数理统计与管理，1997，(06)：26-34.

[5]Wu C F J,Hamada M.Experiments Planning,Analysis,and Parameter Design Optimization[M].北京：中国统计出版社，2003：81-94.

[6]刘飞燕，张建方，崔利荣.关于交互作用知识的一些研究[C].中国现场统计研究会.第一届中国“试验设计与质量改进”会议论文集[A].北京：中国现场统计研究会，2007：180-187.

[7]任露泉.试验优化设计与分析[M].吉林：吉林科学技术出版社,2001：174-175.

[8]王玉枝，张建方.用正交设计方法求解非线性规划区间约束最优化问题的探讨[J].中国科学院研究生院学报,2003，20(03)：290-295.

[9]Hickernell F J，Yuan Y X.A simple multistart algorithm for global optimization[J].Operat Research Transact(China)，1997，2(01)：1-12.

[10]Ai C R，Norton E C.Interaction terms in logit and probit models[J].Econ Lett.2003(80)：123-129.

[责任编辑：郑秀亮 英文编辑：刘彦哲]

Estimating Two Factor Interaction Quickly and Easily

WANG Yu-zhi，XING Chun-feng

(Basic Courses Department，Beijing Union University，Beijing 100101,China)

Because of the complexity of estimating the interaction by experiment design,this paper proposes a new method to estimate the interaction quickly and easily.This method is simple in application and requires small calculation work.It is stable,reliable and precise.Also this paper analyzes the features suitable for the actual application of this method,and explains the underlying mechanism with non-linear quadratic regression.

experiment design；interaction；quadratic regression

国家自然科学基金资助项目(61374082)；北京联合大学新起点项目(zk10201409)

王玉枝(1974-)，女，河北张家口人，中国科学院硕士研究生，北京联合大学基础部教师。

O 212.6

A

10.3969/j.issn.1673-1492.2015.02.001

来稿日期：2014-12-10