具有Allee效应的食饵-捕食模型的最优捕获问题
李文霞,许洪建,李文帅
(1.兰州交通大学数学系,甘肃兰州 730070;2.天津职业技术师范大学数学系,天津 300222;3.石家庄铁道大学材料科学和工程学院,河北石家庄 050000)
具有Allee效应的食饵-捕食模型的最优捕获问题
李文霞1,许洪建2,李文帅3
(1.兰州交通大学数学系,甘肃兰州 730070;2.天津职业技术师范大学数学系,天津 300222;3.石家庄铁道大学材料科学和工程学院,河北石家庄 050000)
建立了食饵含Allee效应的最优捕获模型,证明了系统平衡点的渐进稳定性和全局稳定性,并讨论了生态平衡点的存在性,最后利用Pontryain最大值原理确定了最优捕获策略.
Allee效应;Pontryain最大值原理;最优捕获
所谓Allee效应,即在自然环境中,由于个体很难找到食物或配偶时,种群遭遇相反的密度依赖维持很低的密度,并对生殖发生负作用,甚至最终走向灭亡.
植物[1]、海洋无脊椎动物[2]、哺乳动物[3]等都具有Allee效应.近年来,Allee效应对种群和生态学系统的稳定性影响问题一直是许多专家学者关注的热点,相关研究成果已有很多[4-9],其中大多数文献讨论的是增长函数具有乘法形式的Allee效应.文献[10]考虑了食饵自然增长函数具有加法形式的Allee效应,模型如下:

本文受其启发,将对食饵自然增长函数具有加法形
式的Allee效应的最优捕获问题进行研究,于是得到如下模型:
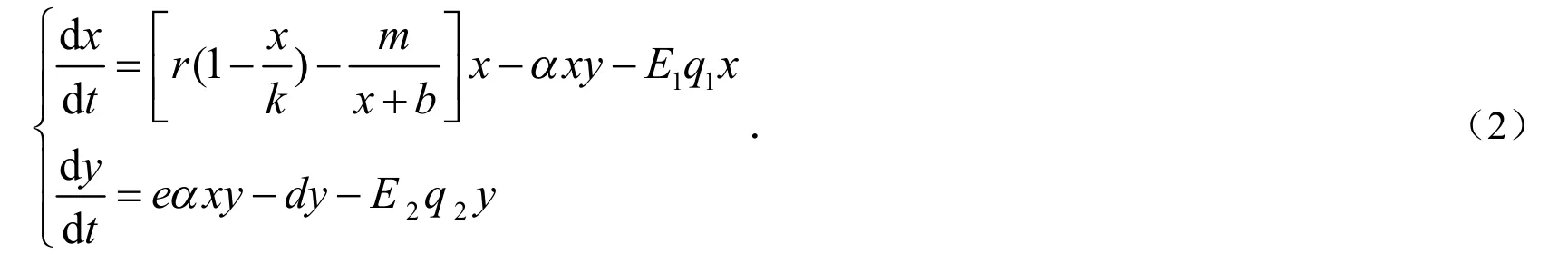
其中,E1,E2分别表示食饵和捕食者的捕获努力度,q1,q2分别表示食饵和捕食者的捕获能力系数,E1,E2,q1,q2均大于0.其它参数生物意义同模型(1).
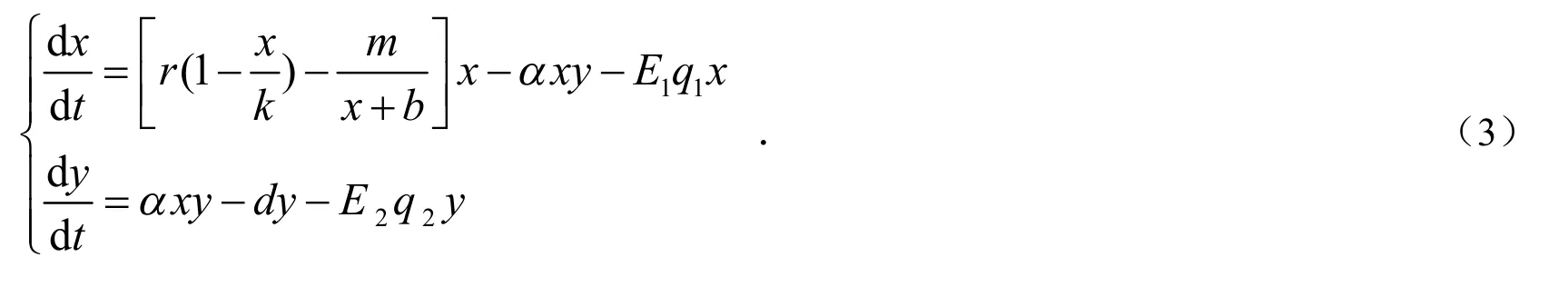
1 正平衡点的存在性及稳定性
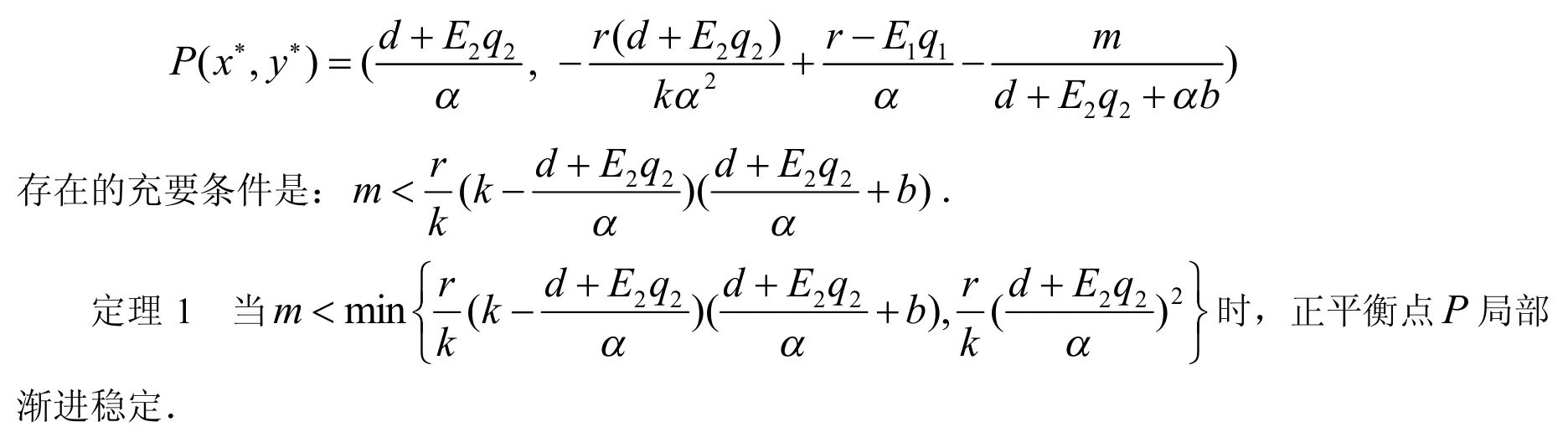
证明:系统(3)的线性近似系统的Jacobian矩阵为:
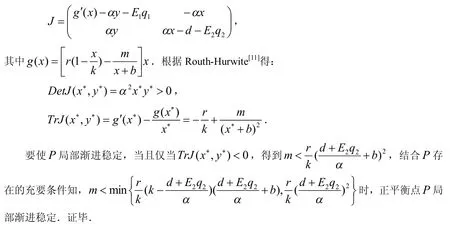
2 系统(3)的全局稳定性
证明:通过构造Lyapunon[11]函数:
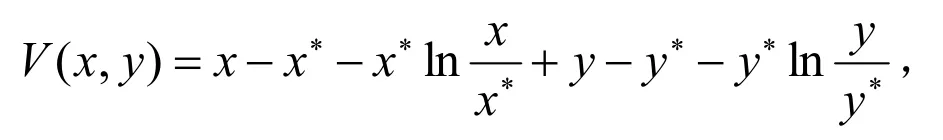
显然,其为正定函数.沿系统(3)对V求导,得:
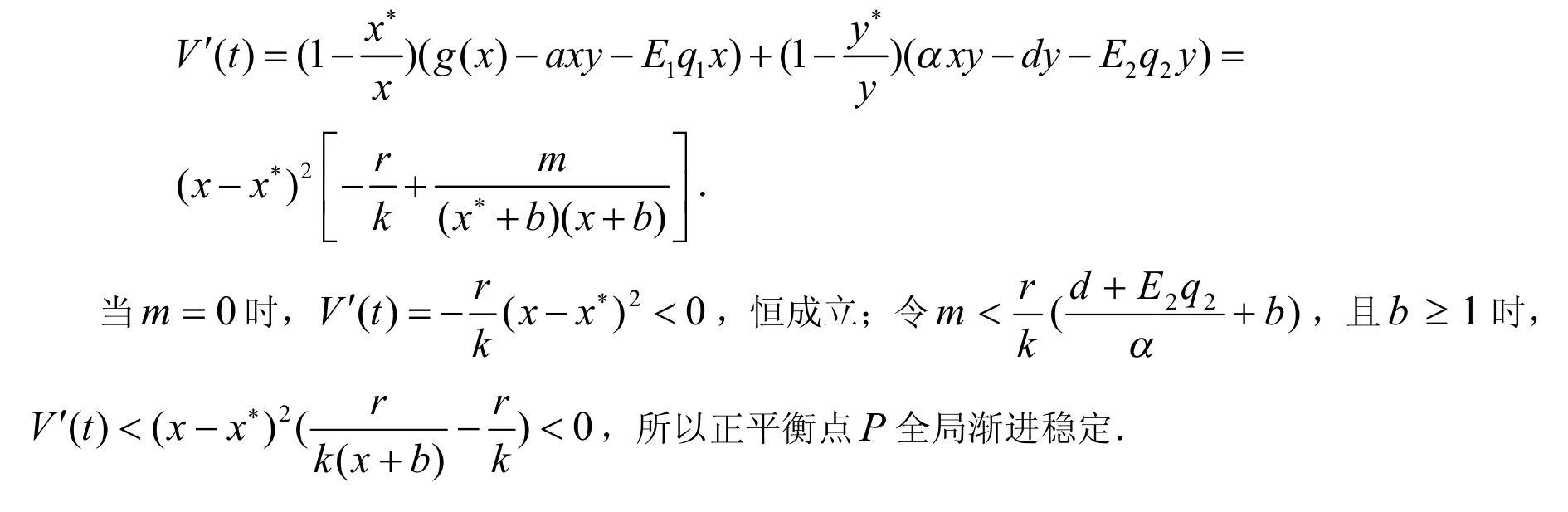
3 生态经济平衡点的存在性
下面在生产模型(3)的基础上,建立生物经济模型.
设p1,p2分别表示资源x,y的价格(元/吨),c1,c2分别表示食饵和捕食种群进行捕获的单位努力度成本,则社会经济收入为:
为了计算简单,假设c1,c2为常数,捕食者和食饵所获得的收入均为正值,即
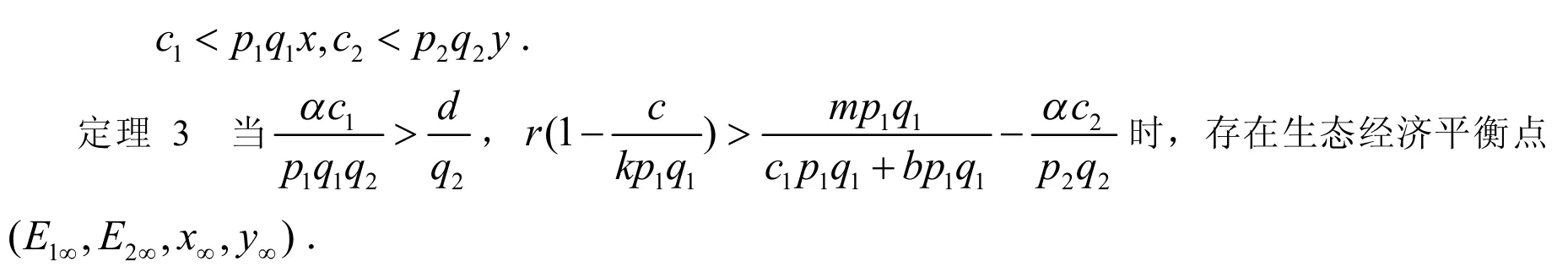
证明:当系统(3)存在平衡点时应满足下面的条件:
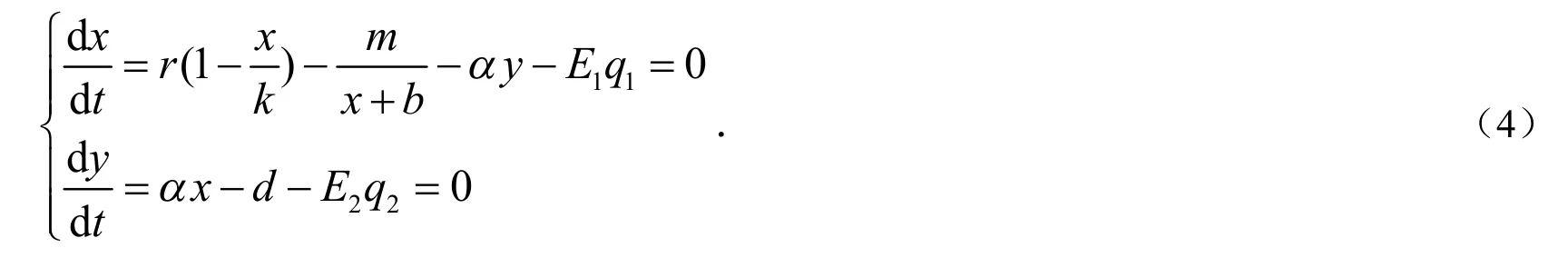
生态平衡点又是经济平衡点,也就是:
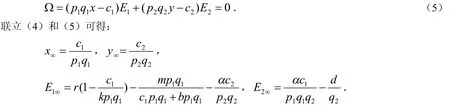
4 最优捕获策略
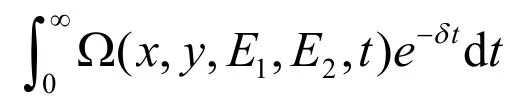

利用比较系数法得非齐次线性方程的通解为:

5 结 论
在自然界中,Allee效应很可能影响食饵或捕食者在生态环境中的稳定性,因此在该系统中讨论最优捕获问题是很切合实际的,这一方面有利于种群的发转,另一方面也可保护环境,维持生态平衡.
[1] Ferdy J B, Austerlitz F, Moret J, et al. Pollinator induced density dependence in deceptive species [J]. Oikos, 1999, 87(7): 549-560.
[2] Stoner A, Ray-Culp M. Evidence for Allee effects in an over-harvested marine gastropod: density dependent mating and egg production [J]. Marine Ecology Progress Series, 2000, 202(3): 297-392.
[3] Kuussaari M, Saccheri I, Hanski I. Allee effects and Population dynamics in the Glanrille fritillary butterfly [J]. Oikos, 1998, 82(17): 384-392.
[4] 李文霞, 雒志学. 具有Allee效应的广义Logistic模型的捕获优化问题[J]. 重庆文理学院学报, 2014, 5(33): 36-39.
[5] 夏降. 含Allee效应的广义Logistic模型之定量开发[J]. 中山大学学报, 1995, 16(2): 33-42.
[6] 古二华. 具有Allee效应种群的最优周期捕获问题[J]. 浙江海洋学院学报, 2009, 28(3): 371-375.
[7] 黄林林, 赵立纯. 基于Allee效应的鱼种群资源管理[J]. 鞍山师范学院学报, 2013, 15(2): 4-7.
[8] 王静, 薛亚奎. 一类具有Allee影响的捕食与被捕食模型[J]. 数学的实践与认识, 2008, 3(10): 136-140.
[9] 任亚静, 雒志学. 一类具有Allee效应捕食系统的最优收获分析[J]. 温州大学学报, 2013, 3(3): 56-62.
[10] 王万雄, 赵灿生, 张艳波. 一类具有Allee效应捕食系统的稳定性分析及模拟[J]. 数学实践与认识, 2013, 43(20): 245-249.
[11] 马知恩. 种群生态学的数学建模与研究[M]. 合肥: 安徽教育出版社, 1996: 23-45.
[12] 邢继祥, 张春蕊. 最优控制理论[M]. 北京: 科学出版社, 2003: 56-60.
Optimal Capture Strategy of a Predator-prey Model with Allee Effect
LI Wenxia, XU Hongjian, LI Wenshuai
(1. Department of Mathematics, Lanzhou Jiaotong University, Lanzhou, China 730070; 2. Department of Mathematics, Tianjin Normal University of Vocational Technology, Tianjin, China 300222; 3. College of Materials Science and Engineering, Shijiazhuang Railway Institute, Shijiazhuang, China 050000)
This paper proves asymptotic stability of the equilibrium point of the system and the overall stability on the basis of the optimal prey capture model with Allee effect. Meanwhile, the existence of ecological equilibrium is discussed then. Finally the optimal capture strategy is determined by means of the Pontryain maximum principle.
Allee Effect; Pontryain Maximal Principle; Optimal Capture Strategy
O175
A
1674-3563(2015)01-0017-06
10.3875/j.issn.1674-3563.2015.01.004 本文的PDF文件可以从xuebao.wzu.edu.cn获得
(编辑:王一芳)
2014-03-17
李文霞(1987- ),女,山西朔州人,硕士研究生,研究方向:生物数学

