基于半监督拉普拉斯适应实验设计的图像分类
熊兴良,樊明宇,洪振杰
(温州大学数学与信息科学学院,浙江温州 325035)
基于半监督拉普拉斯适应实验设计的图像分类
熊兴良,樊明宇,洪振杰†
(温州大学数学与信息科学学院,浙江温州 325035)
基于流形学习理论,通过改变权值的设置将类别信息加到图构造过程中,提出一种新的主动学习算法.在3个真实图像数据集上的实验结果表明,新算法能够取得较好的图像分类效果.
主动学习;流形学习;图像分类
图像分类中需要大量已标签样本来训练分类器,而在实际应用中标注无类别数据样本比较昂贵和费时,特别是对于人脸识别问题.近来主动学习已经成为机器学习和模式识别[1]领域中的一个热点,许多主动学习技术为图像分类和文本分类而提出,例如,直推式实验设计和支持向量机(SVM)[2].以往绝大多数方法都是关于如何发现数据空间的判别结构的[3-4],对几何结构则很少关注.为了研究其潜在的几何结构,人们提出了各种各样的流形学习算法,例如拉普拉斯特征映射、等距特征映射(ISOMAP)[3]、局部保持投影等.基于直推式实验设计,通过使用拉普拉斯构图法并在流形适应核空间里执行任务,以此来研究主动学习,蔡登等人为文本分类[4]提出了一种新的称为流形适应实验设计(MAED)[4]的主动学习算法.本文在半监督学习[5]条件下为图像主动学习提出一种称为半监督拉普拉斯适应实验设计(SSLAED)的新颖流形适应主动学习算法,通过半监督方式构图并将图结构并到流形核中,从而使新的流形结构能够被应用到学习过程中,传统优化实验设计也能够在流形适应核空间中执行.很多主动学习算法在建立本质流形结构并解释其类别信息上不太理想[4],本文所给的新算法能够有效地解决这个问题.
1 背景知识
主动学习最基本的目的:在欧氏空间Rm中给出一个数据集X={x1, x2,...,xn},找出最具信息量的样本子集Z={z1, z2,...,zk}⊂X ,也就是说,如果给点zi( i=1,2,...,k )标签并将其用作训练点,它们应该最能够提高分类器的性能[4].对于这个问题,一般做法是选择最不确定的数据来训练模型或通过挖掘数据的聚类结构来选择最具代表性的点.
1.1 优化实验设计与直推式实验设计
优化实验设计(OED)[6]的研究与实验设计相关,它希望最小化参数模型的总体方差.基于优化实验设计,人们提出直推式实验设计,在已标签和未标签样本上评估期望预测误差.相关研究表明最小化学习函数f的平均期望平方预测误差是直推式实验设计最重要的部分.对于任何数据样本x,yˆ=wˆTx是它的预测观察函数,则在数据集X上的平均期望平方预测误差可以写成如下形式:
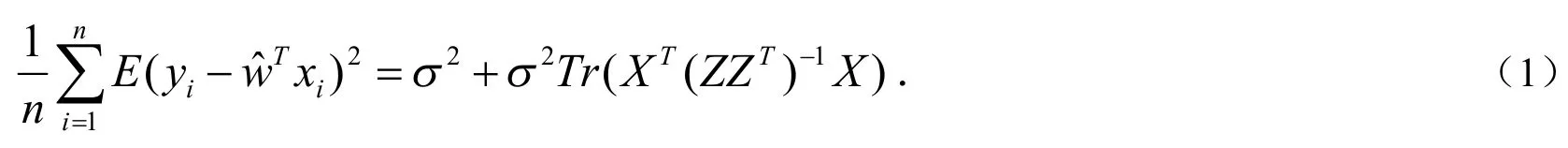
为了最小化平均期望平方预测误差,需要找到一个能够最小化(1)式的子集Z,能够证明这是NP-hard问题,因此不可能找到全局优化量.平均期望平方预测误差的最小化形式也可以写成如下:

(2)式获得的结果是局部优化.通过辅助变量β=(β1,...,βn)引入训练数据集的内在几何关系,(2)中优化问题可以等价地写成如下形式:
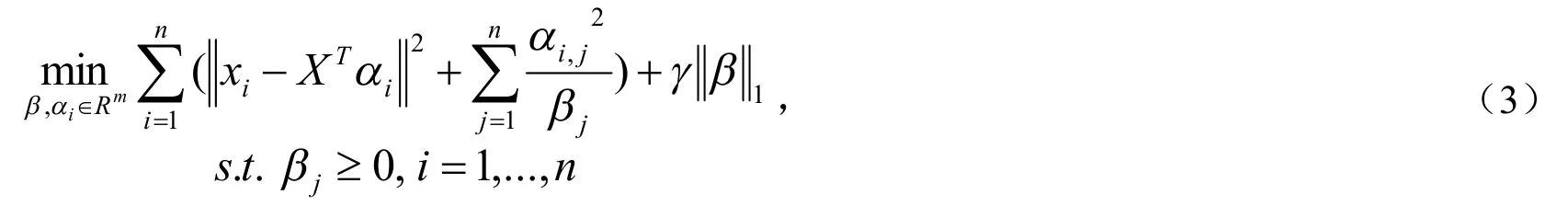
这里α=(α,...,α)T,·表示l范数.l范数的最小化形式β可以产生稀疏向量β,也就
是说β的一些元素将会变为0;如果βj=0,则αi,j=0(i=1,...,n),否则目标函数趋向无穷大,因此第j个样本不能被选中.相关研究表明问题(3)是凸的,因此能够获得全局优化量.
1.2 流形适应实验设计
为了将流形结构引入到主动学习过程中,一般在流形适应核空间里面执行主动学习任务.给出样本x1,…,xn,令Kx=(K( x, x1),…,K( x, xn)),能够知道可再生核是下面的形式:

其中I是单位矩阵,K是n×n核矩阵,满足Ki,j=K( xi, xj),M是正半定矩阵,常数λ≥0用来控制函数的平稳性.(4)式中的关键问题是矩阵M的选择,通过选择基于拉普拉斯构图方法的矩阵M,MAED提出数据独立核以及在流形适应核空间里执行凸直推式实验设计.令K( xi, xj)=φ(xi),φ(xj),这里φ是特征映射.在Sindhwan等人提出的可再生希尔伯特核空间(RKHS)中,(3)中的凸TED优化问题可以写成如下形式:
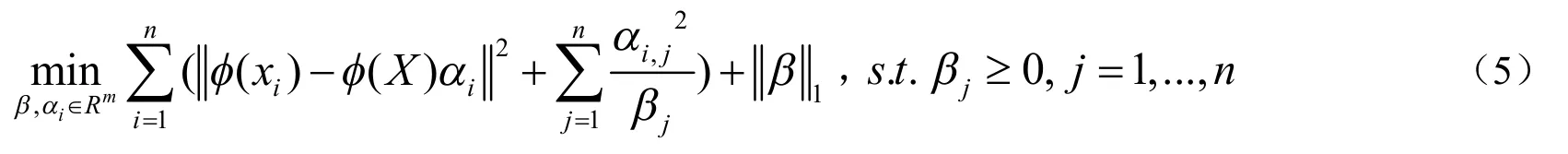
这里φ(X)表示可再生核希尔伯特核空间里的数据矩阵,也就是说φ(X)=(φ(x1),...,φ(xn)).根据βj(j=1,...,n)以打乱次序的方式罗列数据样本并选择最近的k个点,当选择好最具信息的数据点后,任何分类算法都能够被应用到模式分类中去.显然,MAED方法的表现主要取决于矩阵M的选择.
2 半监督拉普拉斯适应实验设计
这部分具体本文的新算法.
2.1 以半监督方式建立一个重构图G
1)在欧氏空间Rm中给出数据集X={x, x,...,x},对于任何已知类别的数据点x,首先
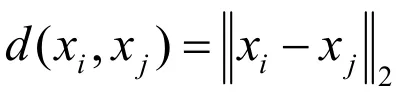
2)计算权值矩阵和重构图,权值矩阵W构造方式如下:
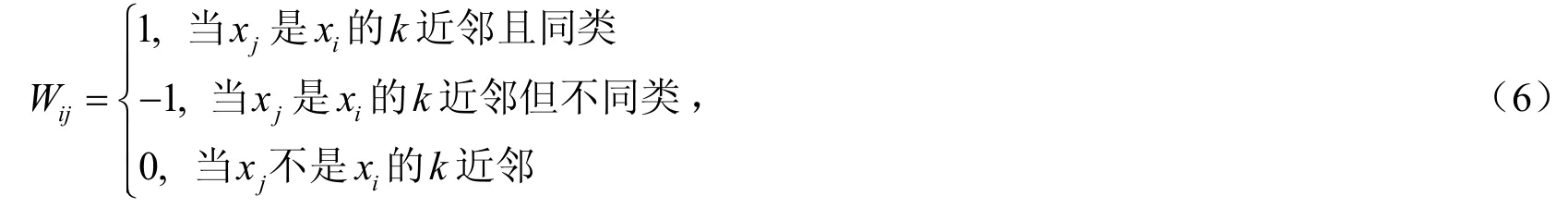
这里权值Wij表示数据点xi的k近邻样本点xj对样本点xi所做的贡献.下面使用拉普拉斯构图方法来构造重构图.在拉普拉斯构图方法中定义了这样一个矩阵:L=D-W,这里D是一个满足Dii=∑jWij的对角矩阵.对于数据集X={x1, x2,...,xn},令G=(X,L)为其重构图.
2.2 新主动学习算法
应用上面建立的图G=(X,L),本文的算法步骤可以总结如下:
输入:在欧氏空间Rm中给出点集X={x1, x2,...,xn},这些点部分带有类别标签信息.
1)以半监督方式先建立一个如(6)式中的权值矩阵W,接着根据已求得的矩阵W以及拉普拉斯构图法构造出重构图G=(X,L);
2)由给出的核类型计算核矩阵K;
3)通过使用L来代替(4)式中的矩阵M,最终获得如下流行适应核:

4)令ui是核矩阵KM的第i列或者第i行向量(因KM是对称的).先令αi,j=1并迭代计算:
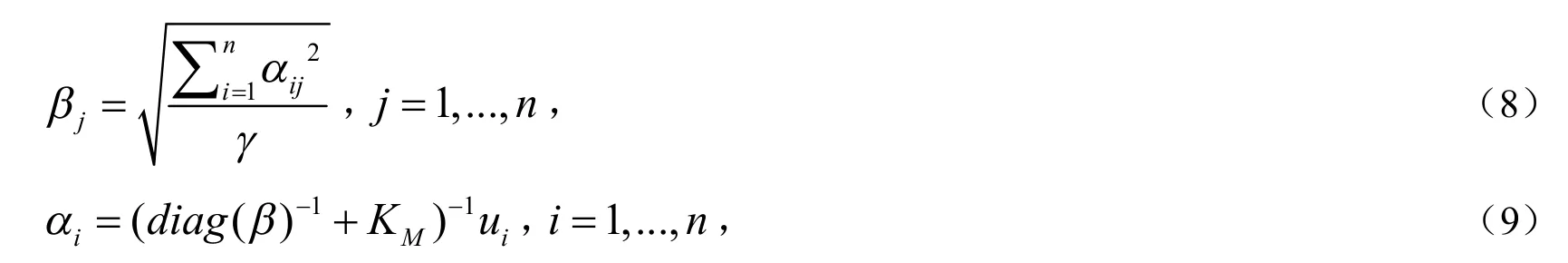
直到收敛;
5)数据选择.当得到βj(j=1,...,n)后,根据βj以打乱次序的方式罗列数据点并且选择最近的k个数据点.
输出:所有数据样本根据其重要性重列,一但选择好最具信息的数据点后,任何分类算法都可以应用到模式识别任务中去.
与MAED算法相比,新主动学习方法同样也是基于流形假设,通过对所有数据点使用一个固定的k近邻范围来定义近邻图,不同之处在于本文的新算法以半监督方式建立流形适应核,在权值矩阵构造方面,充分考虑到数据样本的已知类别信息,这使得其具有更好的鲁棒性.
3 实 验
在这部分,将对本文所提出的主动学习方法(SSLAED)在3个真实数据集上的表现进行评估,并与MAED、一近邻(1-NN)、随机样本选择(Random)这几种分类方法进行比较.其中1-NN方法知道训练样本的所有类别标签并用训练数据集对测试集进行分类;Random方法统一选择样本作为训练数据,本文使用这种方法作为主动学习的基准,所有主动学习算法的效果至少要好于该基准方法.
3.1 数据集描述
本文的实验在3个真实图像数据集:CBCL、MNIST、USPS上进行检验和分析.
MIT CBCL[7]是一个非常著名的数据集,包含2 429张人脸图片和4 548张非人脸图片,每张图片达到19×19分辨率并且被转化成一个361维的向量.数据集包含两种类型的数据点,人脸和非人脸的.
MNIST数据集(http://yann.lecun.com/exdb/mnist)是手写数据集,包括60 000个训练样本,10 000个测试样本.
USPS数据集[8]包含数字类0到9的8位灰度级图片,每类数字有1 100个数据点.这个数据集中的每个数据点是一张16×16像素的手写数字图片,并被转化成一个256维的向量.
3.2 参数选择和实验设置
实验中进行对比的算法的效果主要取决于参数的设置.MAED和SSLAED方法需要邻域大小k作为设置的关键参数.实验表明,对于每个数据集,进行对比算法的表现在大范围邻域内是比较稳定的.在本文的实验中,对SSLAED在所有数据集上其邻域值k统一设置为5,被标签的训练数据比例α从0.1变化到0.9,并且固定参数β= 3.在下面的实验结果图中,α的值采用十分制,例如图中“2”、“4”、“6”、“8”数字分别表示0.2、0.4、0.6、0.8,也就是说,α= 2表示在数据集X中20%的数据是有标签的.
3.3 实验结果及分析
用随机样本方法和1近邻方法作为基准方法,在3个真实数据集上的分类结果如1、图2、图3所示.

图1 数据集CBCL上的实验结果

图2 数据集MNIST上的实验结果
如图1、图2、图3所示,随着标签数据的增多(图中的α增大),分类准确率逐渐变高.毫无疑问,SSLAED算法相比于MAED、Random方法在所有数据集上的表现要好,随机样本方法在大多数情况下表现得最差.下面对在3个数据集上的实验结果进行具体的细节描述.
如图1所示,在CBCL数据集上,SSLAED方法一直表现出远远超过MAED方法和Random方法的分类效果,随着α的增加,当它超过0.25时,SSLAED方法甚至能够表现出比1-NN方法还要好的分类效果.值得注意的是,当训练数据集较小时,SSLAED方法仍然能表现出较好的分类效果,特别是当α= 0.1时,SSLAED方法的分类准确率接近90%,实验出现这种结果可能是因为SSLAED算法考虑到了部分标签数据的缘故.
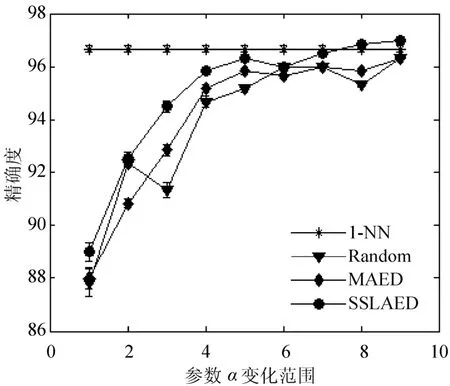
图3 数据集USPS上的实验结果
如图2所示,在数据集MNIST中,多数情况下SSLAED方法比MAED方法的表现要好,而在整个范围内则一直比Random方法好.当α≥0.6时,SSLAED不但比MAED和Random分类效果好而且有着高达98%以上的准确率.当训练样本数据较小时,SSLAED与MAED一样都能够表现出较高的分类准确率.例如,当α= 0.1时,SSLAED有着高达97%的分类准确率.
如图3所示,在USPS数据集中SSLAED一直比MAED的分类效果好.相比于Random方法,除了α= 0.2以及α= 0.6这两种情况,其它条件下SSLAED比Random分类准确率都要高.特别是当α>0.8时,SSLAED分类准确率高达96%以上,且超过了1-NN方法的分类准确率.值得注意的是,当训练数据较小时,SSLAED仍能表现出较好的分类效果,例如当α= 0.1时,图像的分类准确率在88%以上.此外,当0.1≤α≤0.5时,SSLAED对异常值不敏感.
以上已经在CBCL,MNIST,USPS数据集上对4种算法做了对比,可以看出本文的新算法SSLAED在3种真实的数据集上效果显著.这里有两个原因可以解释这点:首先,那些被应用的数据集一直有部分标签样本;其次,在每一类中有大量的数据点并且不同类别的数据相互重叠度较高.
4 小 结
本文通过在流形适应核空间里执行主动学习任务,改变权值矩阵的构造,为图像分类提出了一种新的主动学习算法.在3个真实数据集上的实验结果显示了本文所给的算法比MAED、Random方法要好,特别是当只有一小部分样本被标签的情况.
[1] 张学工. 模式识别[M]. 第3版. 北京: 清华大学出版社, 2010: 1-6
[2] Tong S, Koller D. Support vector machine active learning with application to text classification [J]. Machine Learning Research, 2001, 2: 45-66.
[3] Tenenbaum J B, Silva V D, Langford J C. A global geometric framework for nonlinear dimensionality reduction [J]. Science, 2000, 290(5500): 2319-2323.
[4] Cai D, He X F. Manifold adaptive experimental design for text categorization [J]. IEEE Transactions on Knowledge and Data Engineering, 2012, 24(4): 707-719.
[5] Belkin M, Niyogi P, Sindhwani V. Manifold regularization: a geometric framework for learning from examples [J]. Machine Learning Research, 2004, 7: 2399-2434.
[6] Atkinson A C, Donev A N, Tobias R D. Optimum experimental design, with SAS [M]. Oxford:Oxford University Press, 2007: 184-191.
[7] MIT center for biological and computation learning. CBCL face database [EB/OR]. [2012-10-02]. http://www. ai.mit.edu/projects/cbcl.
[8] Hull J J. A database for handwritten text recognition research [J]. IEEE Transaction on Pattern Analysis and Machine Intelligence [J]. 1998, 16(5): 550-554.
On Image Classification Based on Semi-supervised Laplacian Adaptive Experimental Design
XIONG Xingliang, FAN Mingyu, HONG Zhenjie
(College of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035)
The paper puts forward a new active learning algorithm based on the theory of manifold learning by changing the setting of weights and incorporating class information into the process of graph construction. The experimental result via 3 real-world image datasets demonstrates that the new algorithm is in a position to achieve much better image classification effect.
Active Learning; Manifold Learning; Image Classification
TP391.41
A
1674-3563(2015)01-0011-06
10.3875/j.issn.1674-3563.2015.01.003 本文的PDF文件可以从xuebao.wzu.edu.cn获得
(编辑:王一芳)
2014-02-27
熊兴良(1983- ),男,湖北黄冈人,硕士研究生,研究方向:应用分析与最优化理论.† 通讯作者,hong@wzu.edu.cn

