Shimizu-Morioka混沌系统的电路设计及自适应控制研究

雷腾飞，陈 恒，王 震

(西京学院控制工程学院，陕西西安 325035)

Shimizu-Morioka混沌系统的电路设计及自适应控制研究

雷腾飞，陈 恒，王 震

(西京学院控制工程学院，陕西西安 325035)

针对一类具有四参数的Shimizu-Morioka系统，对系统的平衡点的稳定性进行了研究，并利用分岔图与Lyapunov指数对新增加的两个参数进行了数值分析．运用Multisim软件设计了Shimizu-Morioka系统的混沌电路，基于Lyapunov稳定性理论，设计自适应控制器，实现了系统的混沌同步．Matlab仿真结果验证了所提出同步方法的有效性和可实现性．

Shimizu-Morioka混沌系统；电路仿真；自适应控制

自1963年Lorenz[1]提出第一个混沌模型以来，人们对混沌系统产生了极大的兴趣，并在Lorenz系统的基础上进行改进，发现了许多新的三维混沌系统，如Chen系统[2]，Lü系统[3]、Liu系统[4]等．此后，国内外不少学者提出了以Lorenz系统为基础的若干变种的新混沌系统[5-8]，混沌系统的不断提出进一步促进了人们对混沌现象更深入的认识和研究，丰富和完善了混沌学的研究内容，从而也提高了混沌理论在图像数据加密、保密通信、电力电网动态分析和保护、机械振动故障诊断、振荡发生器设计、信号检测与处理等方面的工程应用能力[9-14]．

由于混沌运动对初值的敏感性和长时间发展趋势具有不可预测性，因此混沌振荡在大多数情况下是有害的，如何有效地抑制或消除混沌现象，已经引起了全球众多学者的广泛关注．1990年，Ott E.等[8]提出一种比较系统和严密的参数微扰方法，即OGY方法．近年来，混沌同步的研究得到了蓬勃发展，该研究方向迅速成为混沌控制领域的研究热点．人们提出了多种混沌同步的思路和方法，如状态反馈方法[9]、自适应控制方法[10]、观测器方法[11]等，取得了良好的控制效果，但所研究的混沌系统多集中在以上几个系统及分数阶系统[16-20]．早在1980年，Shimizu T.和Morioka N.[13]就发明了Shimizu-Morioka系统，到目前为止，此系统的相关研究甚少．

本文对四参数的Shimizu-Morioka系统，通过理论推导、数值仿真系统的吸引子图、分岔图和Lyapunov指数研究了该系统的基本动力学特性；同时为了在实际中更好地应用此系统，设计了系统的硬件电路并进行了仿真实验，进一步说明系统的客观存在性，最后利用Lyapunov函数设计了一个简单的自适应同步控制器，将两个初始值参数未知的混沌系统行为同步，数值仿真证实了该方法的有效性与可实现性．本系统只有六项，比Lorenz系统少一项，故易于工程中实现．

1 混沌系统与分析

根据文[15]所提出的混沌系统，在此基础上再增加两个参数，则四参数的Shimizu-Morioka混沌系统如下：

其中x, y, z为系统变量，a, b, c, d为系统参数，当a=1,b=2,c=0.85,d=0.5，系统（1）存在一个典型的混沌吸引子如图1所示，此时的Lyapunov指数稳态值分别为LE1=0.110931、LE2= -0.000 065 、LE3=-1.460867，维数dL=2.076．

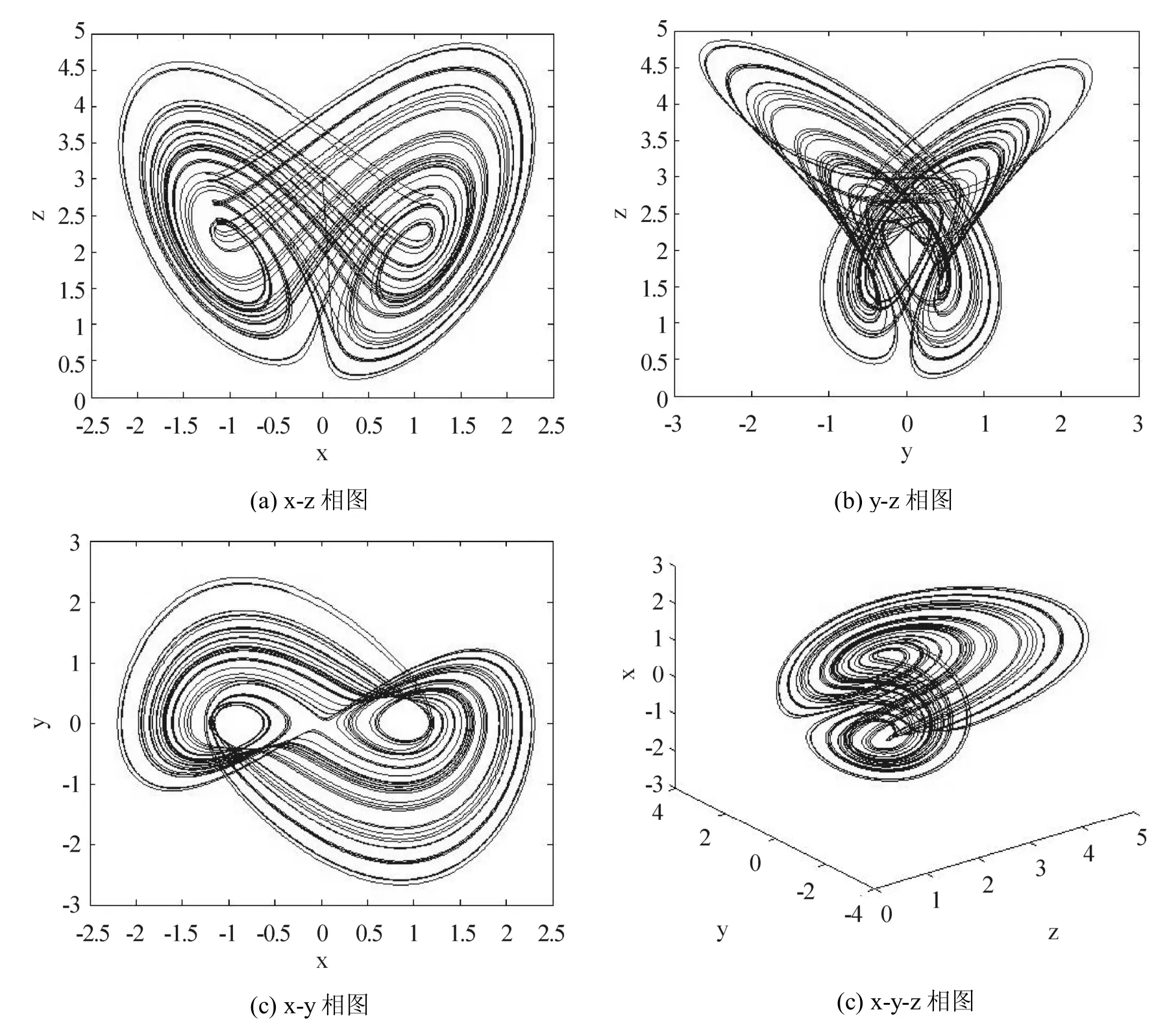
图1 系统吸引子

1.1 耗散性

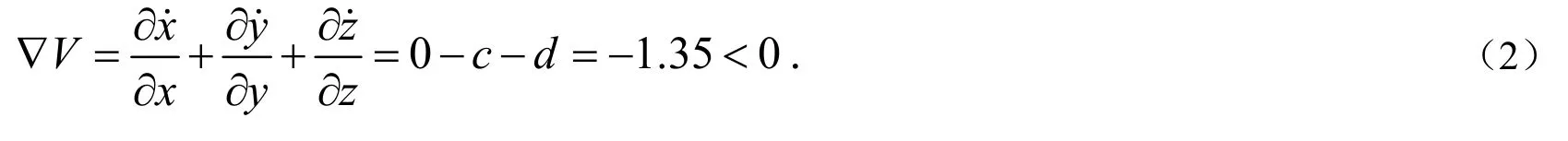
由（1）式得：这就意味着系统（1）具有耗散性，且以指数速率e-1.35t收 敛，当t→∞时，包含系统轨线的每个体积元以指数速率收缩到0．因此，所有系统轨线最终会限制在一个体积为零的集合上，且渐近固定在一个吸引子上，即说明吸收引子存在性．

1.2 平衡点及其稳定性

由此可知，三个平衡点都是不稳定的平衡点，且是双涡卷混沌吸引子．

1.3 Lyapunov指数及分岔图

从系统的三个方向的Lyapunov指数和分岔图，可以直观看出系统运动状态的变化．

固定参数b=2,c=0.85,d =0.5，从图2(a)可以看出，当a∈[0.8,6]系统出现了一个正的Lyapunov指数，系统处于混沌状态，分岔图也可以表明如图2(b)所示．当a∈(6,20]，最大的Lyapunov指数为0，系统处于周期运动形式，如图3所示．

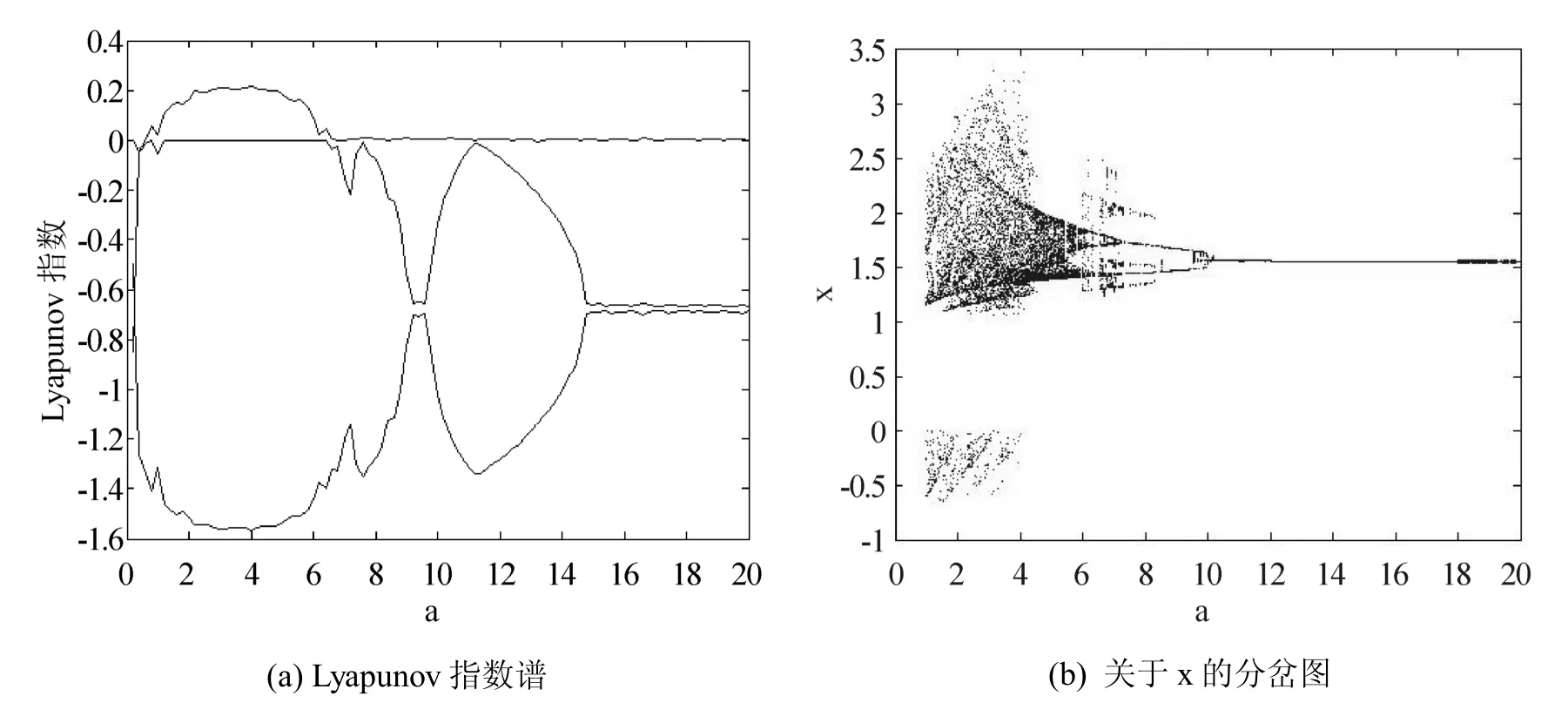
图2 a变化时系统(1)的Lyapunov指数谱与关于x的分岔图

同理，固定参数a=1,c=0.85,d=0.5，分析参数b对系统的影响．当b∈[1,13]系统出现了一个正的Lyapunov指数，系统处于混沌状态，分岔图也可以表明，如图4所示．

2 系统电路原理图及方程

采用NI公司的Multisim软件进行仿真，在仿真软件中，元件库中虚拟器件特性与实际元器件几乎性能一样，Multisim是国际上公认的电路设计软件平台，因此该应用该软件的仿真效果与实际效果是相符的．

图3 a=8时系统相位图

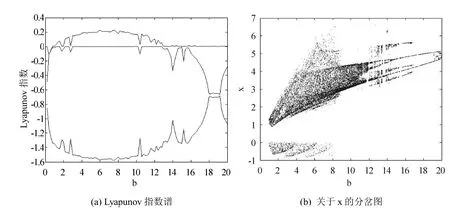
图4 b变化时系统(1)的Lyapunov指数谱与关于x的分岔图

对四参数的Shimizu-Morioka混沌系统（1）进行电路设计，根据系统（1）的状态表达式，设计电路图如图5．系统（1）是由线性电阻、电容、运算放大器LM741和模拟乘法器AD633来实现的．因为LM741与AD633允许工作电压的限制，故将输出电压线性缩小为原来的0.1倍．

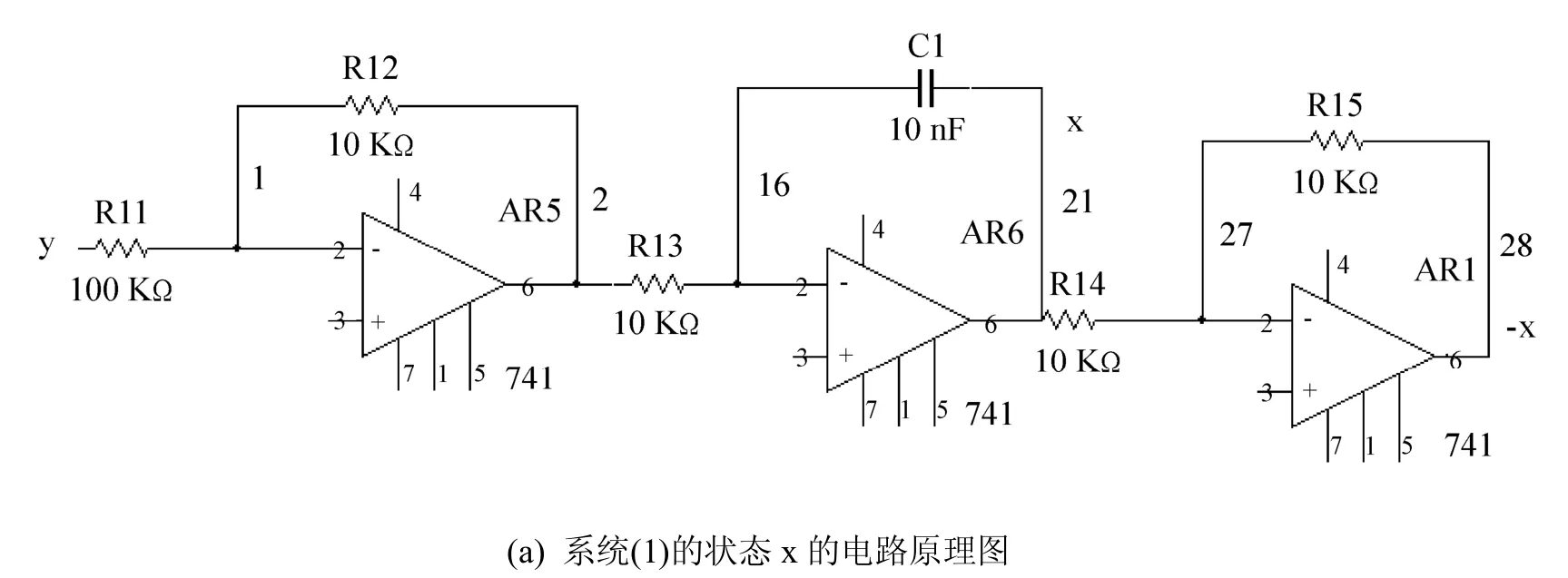
图5 系统(1)的电路原理图

根据电路图，写出其相应的振荡电路方程为：

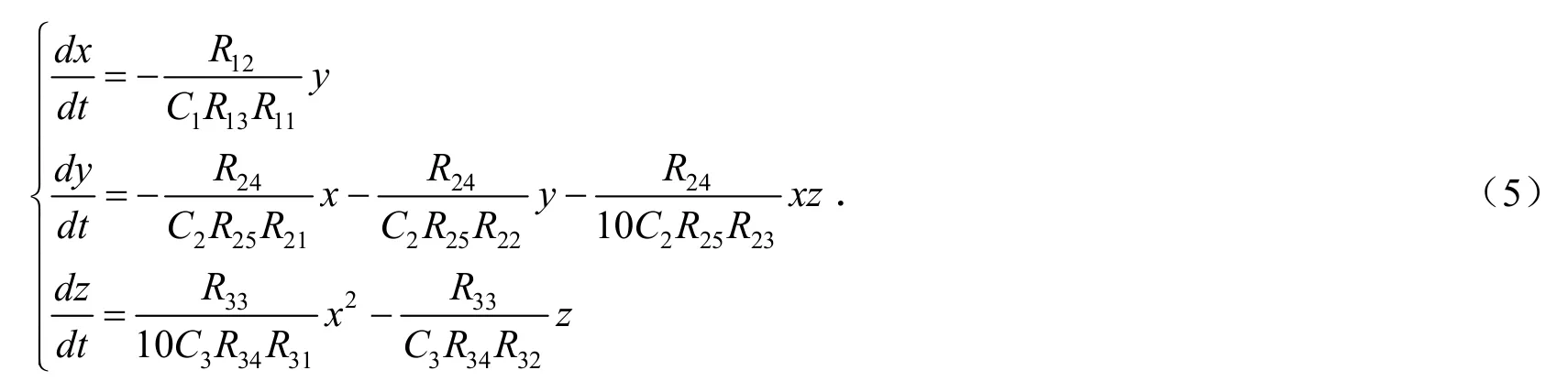
运用Multisim 10对电路进行仿真，将水平轴线进行了调整，显示在示波器上且为实时显示，如图6所示．

图6 系统(5)的相位图

混沌电路的搭建应该注意两个重要问题：

1）对于电阻误差精度的选择，建议选择精密电阻，对于非标电阻可以通过串并实现．

2）对于供电系统的选择，采用线性稳压电源，尽量避免开关电源的使用，因开关电源纹波较大，对输出波形干扰较大．

上述的理论分析、数值仿真、以及电路系统仿真均证明了Shimizu-Morioka混沌系统具有混沌系统共有的一切特征，因为其参数多和电路的可容易实现性，该系统具有更多潜在的应用价值，如电路的抗干扰性，混沌通信和图像加密以及检测等．

3 自适应控制器的设计

为了更好的研究本系统，设计一种简单的同步控制器，加以控制．

定义驱动系统为系统：

4 仿真结果

为了验证上述同步控制器的有效性，对该方法用Matlab进行了仿真．取参数a=1，b=2，c=0.85，未知参数d=0.5，系统出现混沌现象．取两系统的初始条件分别是：x1(0)=0.1，y1(0)=0.1，z1(0)=0.1，x2(0)=1，y2(0)=2，z2(0)=3， d*(0)=0，仿真的同步结果与误差结果如图7、图8所示．由图7图8可知，当t接近14 S左右时，驱动系统与响应系统三个状态量都达到了同步．

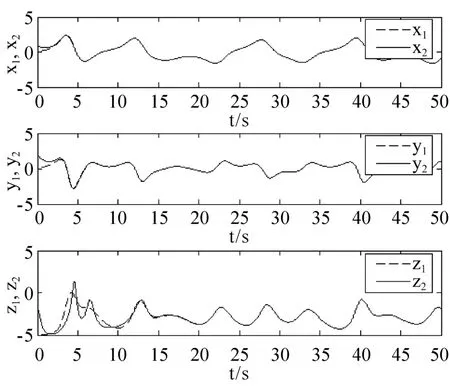
图7 驱动系统与响应系统同步的过程结果

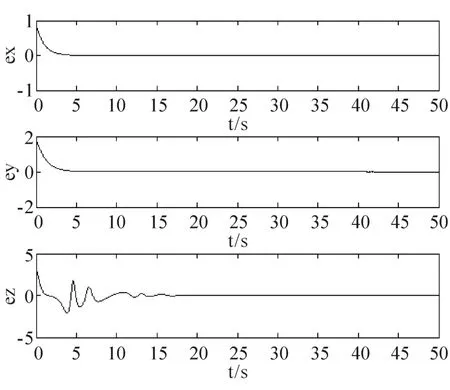
图8 驱动系统与响应系统误差结果

5 结 论

本文对含有四参数Shimizu-Morioka系统，进行数值仿真和电路仿真，发现该系统的混沌吸引子形状有别于Lorenz系统和Chen系统，该系统混沌吸引子形状像是振动翅膀的蝴蝶．通过计算该系统的平衡点及其稳定性、数值仿真和电路仿真验证了该系统丰富的动力学特性．基于Lyapunov稳定性原理，设计了一种自适应同步控制器，实现了Shimizu-Morioka混沌系统的同步．Mtalab仿真结果，证实了该方法的可行性及可实现性．本文研究的系统参数较多，并且可以用电子振荡器电路来实现，所以该系统可广泛应用于电子图像加密等领域．

致谢：本文写作过程中，上海大学机电工程与自动化学院王划教授对本文提出宝贵意见，在此一并致谢．

[1] Lorenz E N. Deterministic nonperiodic flow [J]. J Atmos. Science, 1963, 20(2): 130-141.

[2] Chen G, Ueta T. Yet another chaotic attractor [J]. International Journal of Bifurcation and chaos, 1999, 9(7): 1465-1466.

[3] Lü J H, Chen G R. A new chaotic attractor coined [J]. International Journal of Bifurcation and chaos, 2002, 12(3): 659-661.

[4] Liu C X, Liu T, Liu L. A new chaotic attractor [J]. Chaos, Solitons and Fractals, 2004, 22(5): 1031-1038.

[5] Chen S H, Liu J. Syschronization of an uncertain unified chaotic system via adaptive control [J]. Chaos, Solitons & Fractals, 2002, 14(4): 643-647.

[6] 王繁珍, 齐国元. 一个新的三维混沌系统的分析、电路实现及同步[J]. 物理学报, 2006, 55(8): 4005-4012.

[7] 王兴元, 王明军. 超混沌Lorens系统[J]. 物理学报, 2007, 56(9): 5136-5141.

[8] Ott E, Grebogi C, Yorke J A. Controlling chaos [J]. Physical Review Letters, 1990, 64(11): 1196-1199.

[9] 胡岗. 混沌控制[M]. 上海: 上海科学教育出版社, 2000: 119-125.

[10] 王震, 吴云天. 一类三维混沌系统的计算机仿真控制[J]. 煤炭技术, 2009: 28(9): 177-178.

[11] 姚利娜, 高金峰, 廖旎焕. 实现混沌系统同步的非线性状态观测器方法[J]. 物理学报, 2006, 55(1): 35-41．

[12] 雷腾飞, 陈恒, 王震, 等. 分数阶永磁同步风力发电机中混沌运动的自适应同步控制[J]. 曲阜师范大学学报:自然科学版, 2014, 40(3): 63-68.

[13] 雷腾飞, 陈恒, 王荣, 等. 非均匀气隙永磁同步电机混沌系统的分析与控制[J]. 云南民族大学学报: 自然科学版, 2014, 23(6): 443-446.

[14] 雷腾飞, 陈恒, 王荣, 等. 变形Rikitake双盘耦合发电机系统的动力学分析与控制[J]. 济宁学院学报, 2014, 35(3): 52-56.

[15] Shimizu T, Morioka N. On the bifurcation of a symmetric limitcycle to an asymmetric one in a simple model [J], Phys. Lett. A, 1980, 76: 201-204.

[16] 胡建兵, 韩焱, 赵灵冬. 分数阶系统的一种稳定性判定定理及在分数阶统一混沌系统同步中的应用[J]. 物理学报, 2009, 58(7): 4402-4407.

[17] Gerschgorin S. Über die abgrenzung der eigenwerte einer matrix [J]. Izv. Akad. Nauk. USSR Otd. Fiz.-Mat. Nauk, 1931, 1: 749-754

[18] 王震, 孙卫. 分数阶混沌系统同步及其保密通信[J]. 计算机应用研究, 2012, 29(6): 2221-2223.

[19] 王震, 孙卫. 分数阶Chen混沌系统同步及Multisim电路仿真[J]. 计算机工程与科学, 2012, 34(1): 187-192.

[20] Wajdi M A, Ahmad M H. On nonlinear control design for autonomous chaotic systems of integer and fractional order [J]. Chaos, Solitons and Fractals, 2003, 18: 693-701.

The Research of Circuit Design for Shimizu-Morioka Chaotic System and Its Self-adaptive Control

LEI Tengfei, CHEN Heng, WANG Zhen
(School of Control Engineering, XiJing University, Xi’an, China 710123)

In this paper, the stability of equilibrium point for a Shimizu-Morioka chaotic system with four parameters is studied. By means of the system bifurcation diagram and Lyapunov exponent, the newly-added two parameters are numerically analyzed. In addition, the chaotic circuit of Shimizu-Morioka system is designed with the Multisim software. Finally, the self-adaptative controller is designed based on Lyapunov stability theory so as to realize the chaotic synchronization of the system. The result of Matlab simulation verifys the effectiveness and realizability of the synchronization.

Shimizu-Morioka Chaotic System; Circuit Simulation; Self-adaptive Control

O415.5

A

1674-3563(2015)01-0023-09

10.3875/j.issn.1674-3563.2015.01.005 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：封毅)

2014-05-27

陕西省教育厅自然科学项目(12JK1077)；西京学院科研基金(XJ130117)

雷腾飞(1988- )，男，山东肥城人，硕士研究生，研究方向：混沌电路与混沌控制