基于悬臂梁结构的压电能量收集器的机电转化效率分析

方 超，胡永明，任 博，梁 柱，许春东，顾豪爽，罗豪甦

（1.湖北大学物理与电子科学学院，湖北武汉430062；2.中国科学院上海硅酸盐研究所，上海201800）

基于悬臂梁结构的压电能量收集器的机电转化效率分析

方 超1，胡永明1，任 博2，梁 柱2，许春东2，顾豪爽1，罗豪甦2

（1.湖北大学物理与电子科学学院，湖北武汉430062；2.中国科学院上海硅酸盐研究所，上海201800）

分析钢球和压电悬臂梁之间的碰撞过程，通过压电振子等效电路模型计算与实验数据分析，研究基于PMNT与PZT两种不同材料的悬臂梁压电能量收集器的输入机械冲击能量和输出电能之间的关系，分析各自机电转换效率受机电耦合系数的影响规律，采用钢球下落撞击悬臂梁结构压电振子的方式实现机械能到电能的转换.

能量收集；压电振子；悬臂梁；转换效率

0 引言

近年来，随着微细机械加工技术、微机械电子（MEMS）技术以及无线通讯技术的不断发展，无线传感器以及各种可植入微型传感器快速进入到集成化、微型化和低功耗的时代［1-3］.这些低功耗器件采用传统化学电池供电，由于体积大、寿命短、存储能量有限及更换困难等不利因素，越来越难以满足微功率电子产品的供能需求.为了满足微功率电子产品、无线传感网络、埋植监测系统以及微小型仿生系统等的供电需求，同时避免大量废弃电池污染环境并解决微电子领域电源更换困难的问题，从环境中收集能量并转换为电能加以利用的能量收集技术已成为国内外的研究热点［4］.

在各种环境能量中，机械振动和冲击能量因其广泛存在且具有可观的分布密度，已成为近年来这一研究领域的焦点.根据能量转换原理不同，机械振动发电技术可分为静电式、电磁式及压电式3类.其中，压电发电装置由于机械转换效率较高，易与微机电系统集成，其成本较低、无电磁干扰、结构简单等优势发展最快［5］.本文中基于压电效应，采用钢球下落撞击悬臂梁结构压电振子的方式实现机械能到电能的转换，分析钢球和压电振子之间的碰撞过程，通过悬臂梁式压电能量收集器的物理等效模型及等效电路图的计算与实验数据分析，讨论基于PMNT与PZT两种不同材料的悬臂梁式压电能量收集器输出电能和输入机械冲击能量之间的关系，研究机电转化效率受机电耦合系数的影响规律.

1 实验部分

1.1 悬臂梁式压电能量收集器结构采用悬臂梁式压电微型能量收集器（包含压电悬臂梁与质量块），其优点在于梁是弯曲变形，相较于杆的纵向振动或轴的扭转振动，悬臂梁结构易于激发，能量转换效率较高［6］.为了与较低的环境振动频率匹配，通常在悬臂梁末端加装一质量块，以降低结构的谐振频率.而众多悬臂梁结构中，矩形悬臂梁结构因其结构简单且便于加工制作，是目前压电振动能量收集中最为常用的结构形式之一［7］.

悬臂梁式压电能量收集器通常由一个压电单晶悬臂梁和质量块组成.压电单晶悬臂梁为重叠型结构，由压电晶片与金属基板组成，如图1所示.其中，l表示悬臂梁的长度；tp表示压电晶片层的厚度；ts表示金属基板的厚度；M表示质量块的有效质量；F表示作用于悬臂梁末端的外界激励.当压电悬臂梁的末端受到作用力或达到一定的位移量时，由压电材料的正压电效应可知，在压电悬臂梁的上下极板上会产生正负相反的电荷并形成电场，从而实现机械能到电能的转换.

从钢球自由下落开始计时，在t=0时刻钢球击中悬臂梁末端，钢球和悬臂梁末端一起向下运动，钢球的动能逐渐转为悬臂梁的弯曲势能，达到最大弯曲程度后，悬臂梁末端的弹力推动钢球开始向上运动，直至t=Tc时刻悬臂梁回到平衡位置，钢球飞离悬臂梁，压电振子开始以无钢球的原始谐振频率振动，在t＞Tc的整个过程中，压电振子的振动呈指数衰减形式直至为零.

1.2 悬臂梁式压电能量收集器物理模型及等效电路图对压电悬臂梁和质量块组成的机械系统进行物理等效，得到系统的物理等效模型，如图2所示［8］，其中M表示质量块的有效质量，k0表示压电悬臂梁的有效刚度，η为阻尼，z表示悬臂梁的振动位移，z0表示基板位移.

图1 压电能量收集器悬臂梁结构示意图

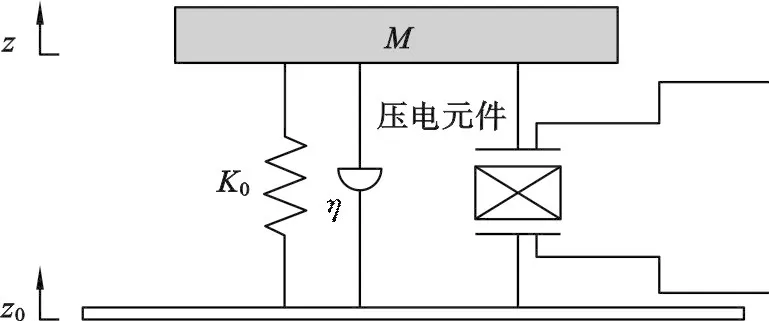
图2 悬臂梁式压电能量收集器物理模型图

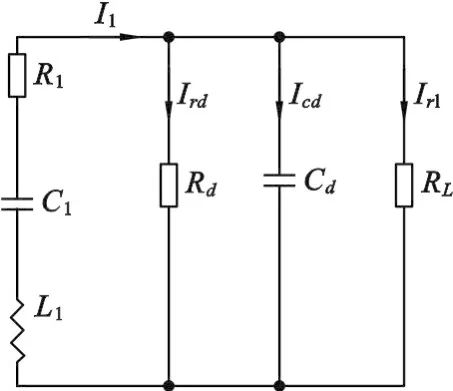
图3 悬臂梁式压电能量收集器等效电路图

根据能量收集系统的机电耦合特性，对图2所示的物理模型进行电器等效［9］，将机械子系统的各个机械特性等效为电器元件，得到系统的电器等效电路图，如图3所示.图3中，等效电感L1与压电悬臂梁中质量块的有效质量M有关，等效电容C1、等效电阻R1分别与压电悬臂梁的顺度系数s和阻尼系数η有关.Cd表示钳位电容，Rd为介电损耗对应的等效电阻，输出电压V0在负载两端，Ird、Icd、Irl表示分支电路上的电流.当0＜t＜Tc时，L1，C1，R1，Cd和Rd由悬臂梁和钢球组成的整体弯曲模式下测量其导纳特性来确定，并且分别被重新标记为L1A，C1A，R1A，CdA和RdA；当t＞Tc时，L1，C1，R1，Cd和Rd由悬臂梁弯曲模式下测量其导纳特性来确定，并重新标记为L1B，C1B，R1B，CdB和RdB.作为计算的初始状态，电流I1是在t=0提供给电感L1A，以便在电感中的电磁能量等于输入初始能量wi，这里wi等于钢球在初始状态的势能，并等于mgh（g是重力加速度）.Tc是电流I1第一次在负方向变为最大的时间瞬变点，因为电流是正比于振动速度的.L1A，C1A，R1A，CdA和RdA改变为L1B，C1B，R1B，CdB和RdB.在Tc时刻，电路中的电流和电压的连续性被保持.

1.3 压电能量收集器悬臂梁结构的参数设置实验中，悬臂梁的金属基板长77.0 mm，厚度0.5 mm.采用尺寸相同即20.0 mm×5.0 mm×0.5 mm、材料不同的PMNT和PZT分别作为压电振子，且置于金属基板不同的位置.置于前端：紧邻夹持端20.0 mm处，如图4(a)；置于中间：处在金属基板中间位置20.0 mm处，如图4(b)；置于后端：紧邻自由端质量块20.0 mm处，如图4(c).其中，夹持占金属基板长度7.0 mm，自由端质量块占金属基板长度10.0 mm.压电能量收集器的电压输出端连接到示波器（示波器本身内阻为10 Mohm）.钢球（质量m=4.0 g）在高于振子末端h处.

图4 压电材料位置图

2 结果与讨论

通过实验，悬臂梁式压电微型能量收集器输出的电压波形如图5所示.

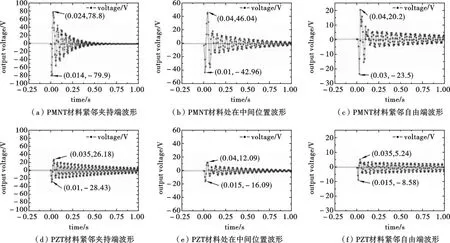
图5 输出电压波形图

从图5中可以看出，同样的激励作用，同样尺寸、同样结构模型的压电振子，PMNT材料峰值电压是PZT材料峰值电压的3倍多.

通过阻抗分析仪，可以得到压电振子的导纳特性的各种参数，见表1.其中fr是谐振频率，fɑ是反谐振频率，B是电纳，D是介电损耗.从表1可知，谐振频率fr较低，多数在20 Hz左右，适合低频应用.

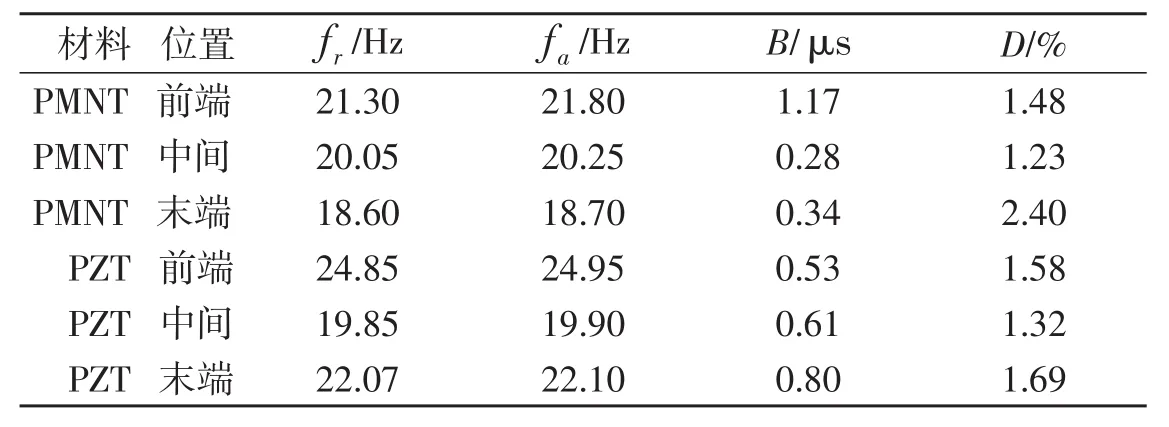
表1 压电振子导纳特性参数

实验测量中，采用激光微位移计测出钢球与压电振子接触共振，得到金属基板首次恢复到平衡位置处的瞬时速度v1及钢球飞离的瞬时速度v2，其中v1=v2，因此可以得到钢球在飞离后带走的动能E1.

压电振子输出电能we与机械冲击能量w1的比值为转化效率，其中，we是压电振子在钢球飞离后首次最大输出电压处的能量，w1是钢球初始能量减去飞离动能后的剩余机械能.由公式（1～7）可以得到机电耦合系数k及转化效率η的值.PMNT与PZT基机电耦合系数k与转化效率η的实验数据关系曲线如图6所示.

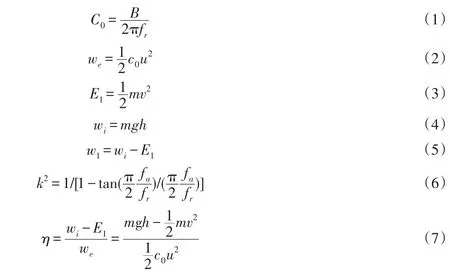
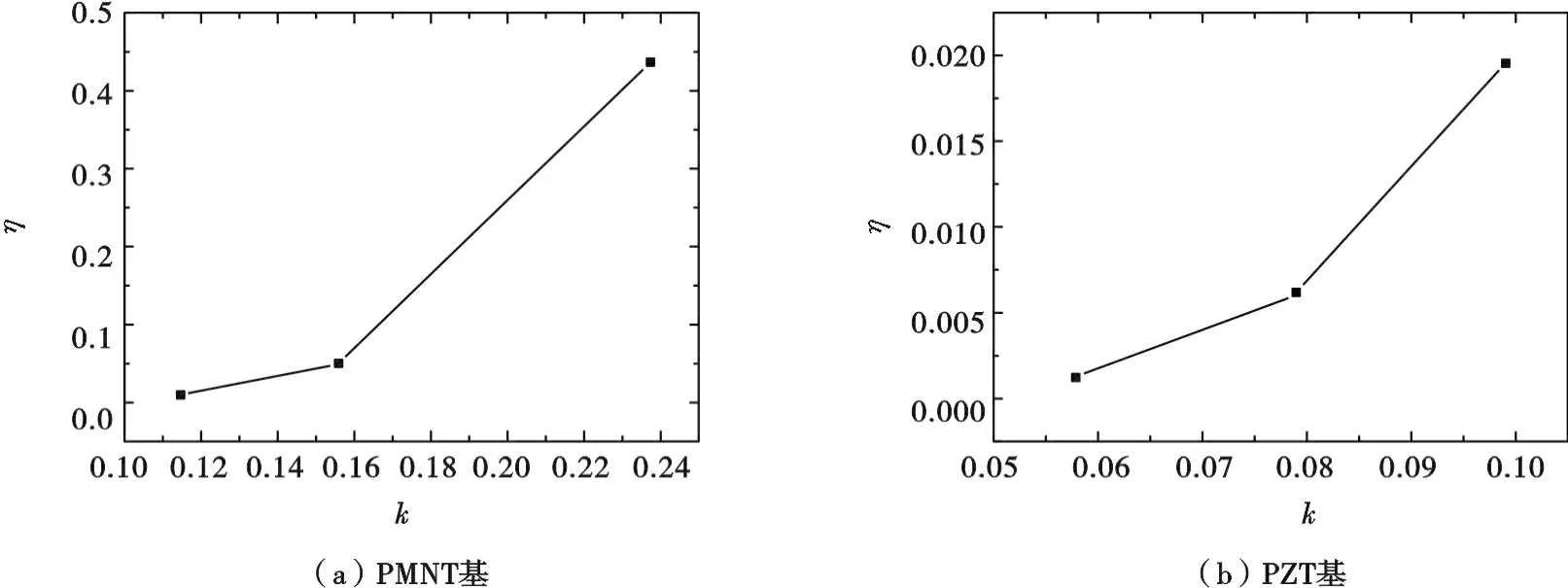
图6 PMNT基与PZT基机电耦合系数k与转化效率η的实验数据关系曲线图

由图6中可以看出，PMNT及PZT基悬臂梁压电能量收集器的机电转化效率η随着机电耦合系数k的增大而不断增大.同时可以看出，在相同尺寸、相同振动模式下，PMNT基压电悬臂梁是PZT基压电悬臂梁的转换效率η的20倍，且PMNT基压电悬臂梁在机电耦合系数为0.24时机电转换效率达到43.76%，具有很高的输出性能.

3 结论

本文中通过分析钢球下落撞击压电悬臂梁的过程，建立由压电悬臂梁和质量块组成的机械系统的物理等效模型，研究其能量收集特征，分析机电转换效率η与机电耦合系数k的关系.在同种材料下，随着机电耦合系数k的增大，机电转换效率η逐渐增加；对于不同种类材料，相同结构、相同尺寸和相同激励下，PMNT基压电悬臂梁的转换效率η的值远比PZT基压电悬臂梁的值大.悬臂梁式压电能量收集器在低频状态下具有很好的电能输出.

［1］Liang Z，Xu C，Ren B，et al.A low frequency and broadband piezoelectric energy harvester using asymmetrically serials connected double clamped-clamped beams［J］.Jpn J Appl Phys，2014，53:087101.

［2］Xu C，Ren B，Liang Z，et al.Nonlinear output properties of cantilever driving low frequency piezoelectric energy harvester［J］.Appl Phys Lett，2012，101:223503.

［3］Xu C D，Ren B，Di W N，et al.Cantilever driving low frequency piezoelectric energy harvester using single crystal material 0.71Pb(Mg1/3Nb2/3)O3-0.29PbTiO3［J］.Appl Phys Lett，2012，101:033502.

［4］Kim H，Kim J.A review of piezoelectric energy harvesting based on vibration［J］.Int J Precis Eng Manuf，2011，12:1129-1141.

［5］Anton S R，Sodano H A.A review of power harvesting using piezoelectric materials(2003-2006)［J］.Smart Mater Struct，2007，16(3):R1-R21.

［6］Arnold D P.Review of microscale magnetic power generation［J］.IEEE T Magn，2007，43(11):3940-3951.

［7］袁江波，谢涛，单小彪，等.压电俘能技术研究现状综述［J］.振动与冲击，2009，28(10):36-41.

［8］刘祥建，陈仁文.压电振动能量收集装置研究现状及发展趋势［J］.振动与冲击，2012，31(16):169-176.

［9］于慧慧，温志渝，温中泉，等.宽频带微型压电式振动发电机的设计［J］.传感技术学报，2010，23(5):643-646.

（责任编辑 郭定和）

Electromechanical conversion efficiency of piezoelectric energy harvester based on cantilever structure

FANG Chao1，HU Yongming1，REN Bo2，LIANG Zhu2，XU Chundong2，GU Haoshuang1，LUO Haosu2
(1.School of Physics&Electronic Science，Hubei University，Wuhan 430062，China；2.Shanghai Institute of Ceramics，Chinese Academy of Sciences，Shanghai 201800，China)

The impact process of the steel ball and the cantilever structure was analyzed.The relationship between the output electrical energy and input mechanical energy based on cantilever piezoelectric energy harvester of two various materials of PMNT and PZT was investigated by piezoelectric oscillator equivalent circuit model calculations and experimental data.The influence of coupling coefficient on electromechanical conversion efficiency was also analyzed.The conversion of mechanical energy into electrical energy was realized by a steel ball free-falling and impacting the cantilever structure.

energy harvest；piezoelectric vibrator；structure of cantilever beam；conversion efficiency

TB34

A

10.3969/j.issn.1000-2375.2015.05.010

1000-2375（2015）05-0451-05

2015-01-12

国家自然科学基金（61274073）资助

方超(1987-)，男，硕士生；胡永明，通信作者，副教授，E-mail：yongming.hu09@gmail.com