变系数EV模型ND样本加权和的相合性

许 雪，程 龚

(湖北大学数学与统计学学院，湖北武汉430062)

变系数EV模型ND样本加权和的相合性

许 雪，程 龚

(湖北大学数学与统计学学院，湖北武汉430062)

利用ND序列的Bernstein型不等式和截尾的方法，研究变系数EV模型的ND样本加权和的相合性问题，获得ND样本加权和Wni(t0)Yi的强、弱相合性，推广独立随机变量加权和的相合性.①

变系数EV模型；ND样本；加权和；相合性

0 引言

定义[1]称随机变量X1,X2,…,Xn是ND(Negatively Dependent)的，若对任意的x1,x2,…,xn∈R有

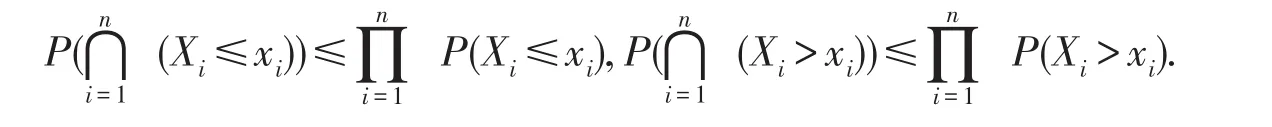
如果对任意的n≥2,X1,X2,…,Xn都是ND的，则称随机变量序列{Xn;n≥1}是ND列.

自1993年Bozorgnia等[1]提出ND列的概念以来，ND列引起了越来越多的学者的关注.文献[2]中举例说明了NA序列一定是ND序列，但ND序列不一定是NA序列，这说明ND序列是比NA序列更弱、更广泛的一种随机变量序列.因此，对ND列的研究在理论和实践中都是有意义的.目前，对ND列的概率性质的研究已取得了一些成果，在多元统计分析、可靠性理论及渗透模型等方面有广泛应用［1-3］.

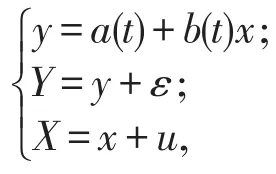
设t0∈(0,1)，要对t0处的ɑ(t0),b(t0)进行参数估计.然而我们不可能在t0处作n次观测，只能在t0处附近作n次观测.设t1,t2,…,tn是[0,1]上n个设计点，满足0≤t1＜t2＜,…,＜tn≤1.

对每个点ti处(Y,X)作观测，得到n组观测值(Yi,ti,Xi)(i=1,2,…,n).当我们利用这n组观测值来估计t0处的参数ɑ(t0),b(t0)时，此时应该必须注意到ti处的观测值(Yi,ti,Xi)(i=1,2,…,n)相对于t0来说他们的重要程度并不一样，这种重要程度可用实变量ti的权函数Wni(t0)来度量.下面我们给出权函数的定义：

设(Yi,ti,Xi)(i=1,2,…,n)是取自母体(Y,X)的样本，t1,t2,…,tn是[0,1]上的n个设计点，t0是(0,1)内的某一个点，实变量t1,t2,…,tn的函数Wni(t0)=Wni(t0,t1,t2,…,tn)(i=1,2,…,n)称为实变量函数(简称为权函数)，如果它满足:

选定一维概率密度函数k(·)及宽窗hn∈(0,1/2),hn→0(n→∞)，则有

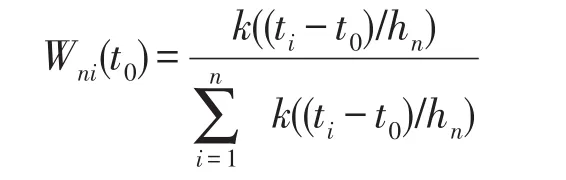
文献[5]中提出了这样一个问题:在何种条件下，当n→∞时有Wni(x0)Yi→E(Y|X=x0),a.s..

欧阳光［6]研究了上式中的权函数Wni(x0)实变量核权函数Wni(t0)时，独立随机变量序列{Yi;1≤i≤n}加权和Wni(t0)Yi的相合性，文献[7]中研究了NA同分布序列{Yi;1≤i≤n}加权和的相合性.笔者在其基础上进行推广，研究变系数EV模型的ND样本{Yi;1≤i≤n}加权和的相合性，获得与独立随机变量样本加权和相同的结论.

1 引理

为了得出本文中的主要结论，我们先给出一些相关的引理.

引理1[1]设{Xn;n≥1}是ND的，对任意的m≥2,A1,A2,…,Am是集合{1,2,…,n}的两两不交的非空子集.

如果fi,i=1,2,…,m是对每个变元都非降(或都非升)的函数，则f1(Xj,j∈A1),…,fm(Xj,j∈Am)仍是ND的.

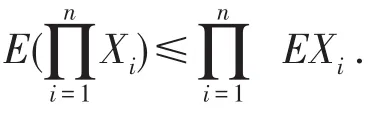
特别地，设随机变量{Xn;n≥1}是ND列，t1,t2,…,tn都是非正或者非负的实数，则有

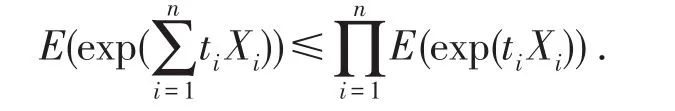
引理3[2](Bernstein不等式)设随机变量{Xn;n≥1}是ND列，EXi=0,|Xi|≤biɑ.s.(i=1,2,…,n),t＞0为实数，且满足≤1，则对任意的ε＞0，有

引理4的证明由条件，对任意的ε＞0及充分大的n知

取t=4ε-1logn＞0，则t满足引理3的要求，因此

引理5[8](推广的Borel-Cantelli引理)

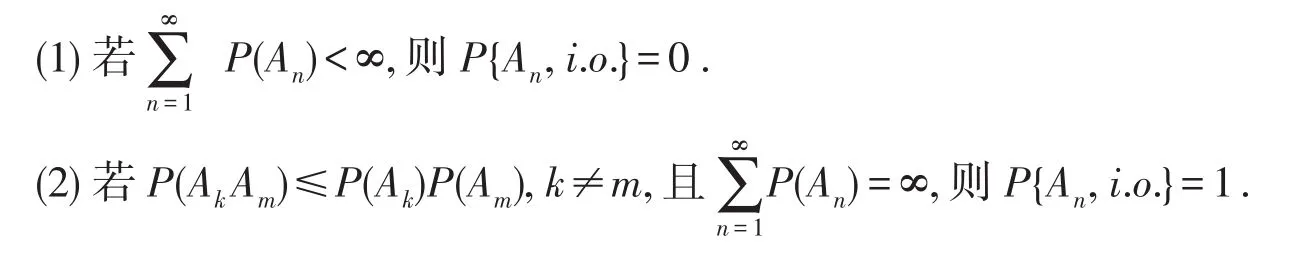
2 主要结果及证明

定理1设{Yi;i≥1}为同分布的ND样本序列，且存在M＞0，使得Vɑr(Y)≤M，若对任意实变量核权函数{Wni(t0);1≤i≤n}存在正数C，使得

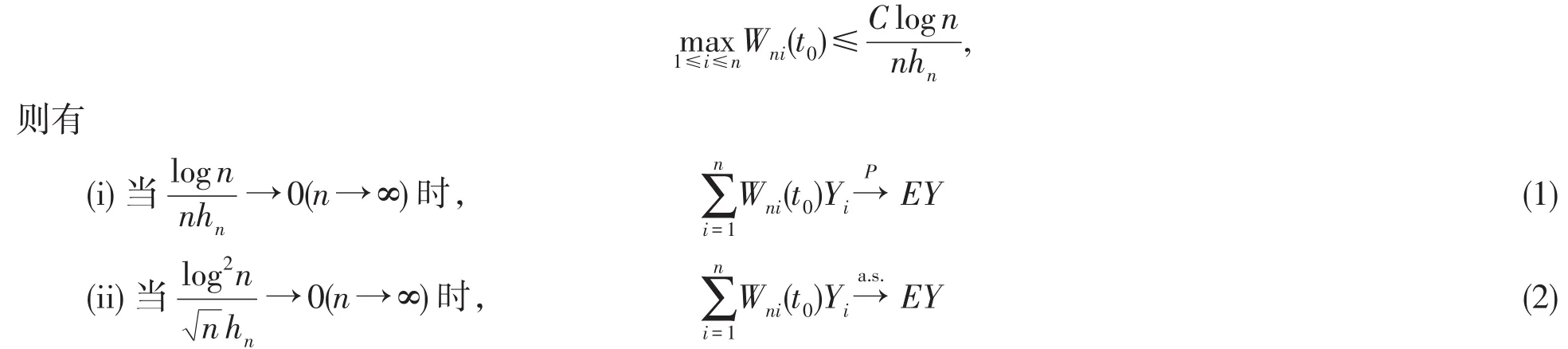
而E(Yi-EYi)=0.Vɑr(Yi-EYi)=Vɑr(Yi)≤M,i=1,2,…,n，因此，不失一般性，假设EY=0.

先证(3)式，记Xni=Wni(t0)(-E)，bn=Wni(t0).由Wni(t0)＞0和的定义，结合引理1知{Xni;1≤i≤n}仍是零均值同分布ND序列.由于

由上面两式可得

由引理4知，对任意的ε＞0及充分大的n，有

由Borel-Cantelli引理可知，对任意的ε＞0及充分大的n时，有

即(3)式成立.

从而(4)式成立，定理1得证.

说明：由于ND序列是比独立序列和NA序列更弱的、更广泛的一种随机变量序列，所以该定理是独立随机变量序列和NA序列情形的推广.

［1］Bozorgnia A，Patterson R F，Taylor R L.Limit theorems for ND r.v.’s［R］.Athens:University of Georgia，1993.

［2］Wu Q Y，Jiang Y Y.The strong consistency of M estimator in a linear model for negatively dependent random samples［J］. Communications in Statistics:Theory and Methods，2011，40(3):467-491.

［3］Wu Q Y.Complete convergence for negatively dependent sequences of random variables［J］.Journal of Inequalities and Applications，2010，Article ID 507293.

［4］Gui H，Chen S X.Empirical likehood confidence region for parameter in the errors-in-variables models［J］.Journal of Multivariate Analysis，2003，84(1):101-115.

［5］陈希儒，王松佳.近代实用回归分析［M］.南宁:广西人民出版社，1984：237-247.

［6］欧阳光.独立随机变量序列加权和的相合性［J］.数学理论与应用，2005，25(1):109-113.

［7］付艳莉，吴群英.NA同分布序列加权和的相合性［J］.吉林大学学报：理学版，2010，25(1):57-62.

［8］吴群英.混合序列的概率极限理论［M］.北京:科学出版社，2006.

（责任编辑 赵 燕）

The consistency for weighted sums of ND sample in varying-coefficient EV models

XU Xue，CHENG Yan
(Faculty of Mathematics and Statistics，Hubei University，Wuhan 430062，China)

We study the consistency for weighted sums of ND sample in varying-coefficient EV models by using ND sequence’s Bernstein inequality and truncated method.As a result，we obtain strong and weak consistency for weighted sums of ND sample and extend the consistency for weighted sums of independent random variables.

varying-coefficient EV models；ND sample；weighted sums；consistency

O212.2

A

10.3969/j.issn.1000-2375.2015.05.008

1000-2375（2015）05-0442-05

2015-04-15

许雪（1992-），女，硕士生，E-mail：1029810565@qq.com