退禁闭相变和孤子性质的研究

董仁达，舒 崧，张 辉

（湖北大学物理与电子科学学院，湖北武汉430062）

退禁闭相变和孤子性质的研究

董仁达，舒 崧，张 辉

（湖北大学物理与电子科学学院，湖北武汉430062）

研究有限温度密度下的FL模型，通过温度场论的标准方法，得到有限温度密度下的有效势.在FL模型中，重子内部亚稳态真空与外部物理真空有效势相等时退禁闭相变发生.据此在有限温度密度下进行计算，得到FL模型中的退禁闭相图.研究发现，该模型在强子相一直有稳定的孤子解，发生退禁闭相变后孤子解消失，孤子的变化与退禁闭相变的物理图像一致.

退禁闭相变；FL模型；孤子；温度场论

0 引言

现代粒子物理学认为，物质的基元是夸克与轻子，然而实验上可以观测到自由存在的轻子，例如电子，却从来没能观测到自由存在的夸克.夸克总是以强子束缚态的形式出现，3个夸克组成重子，两个组成介子，为什么作为基本粒子的夸克不能自由出现，夸克禁闭或色禁闭是高能物理的一个基本问题.理论上认为在极端高温高密的条件下，核物质会转变为一种新的物态——夸克胶子等离子体（QGP）.在这种形态下夸克胶子可看作类自由的粒子，不再局限于强子袋内.在实验上，可通过加速重核，例如金原子核，使获得极大动能的重核束流相撞，会产生瞬间存在的高温高密火球，这时在理论上认为会产生QGP.进行重离子碰撞实验的主要目的就是产生QGP并研究它的性质.

量子色动力学QCD是描述强相互作用的基本理论，然而由于禁闭与手征对称性的自发破缺，QCD很难直接用于研究低能下的物理问题.在低能下，QCD格点计算得到的结果是很可靠的，但由于其工作非常依赖于大规模高性能计算机的运算，不便于理论解析研究，因而很多物理学工作者从具备QCD重要性质的有效模型出发，用温度场论的方法引进温度密度效应，进而讨论有关物理问题.Friedberg-Lee（FL）模型，此模型是上世纪七十年代由李政道等人提出用于研究禁闭及孤子性质的有效模型［1］，又称为非拓扑孤子模型，在平均场近似下Wilets广泛地研究模型在真空环境中的性质［2］.FL模型通过其孤子解非常成功地给出强子的静态性质［3-4］.孤子又称为孤立波，传播过程速度和位形都维持不变，孤子是解非线性微分场方程组得到的一种稳定的能量有限的不弥散解，从物理角度看是场的能量在位形空间的一种局域分布.近些年来FL模型又扩展到有限温度密度下研究退禁闭相变［5-7］，很多研究者关注FL模型在有限温度密度下的有效势.

本文中关心高温下的退禁闭相变以及相变过程中孤子性质的变化，采用有限温度场论的标准方法引进温度密度效应［8］，通过有限温度密度下的热力学势讨论退禁闭相变，并给出退禁闭相图，同时将数值计算不同温度密度下的孤子解，讨论孤子的变化及其与退禁闭相变的关系.

1 物理真空中的FL模型

在零温零密条件下，FL模型的拉格朗日密度为

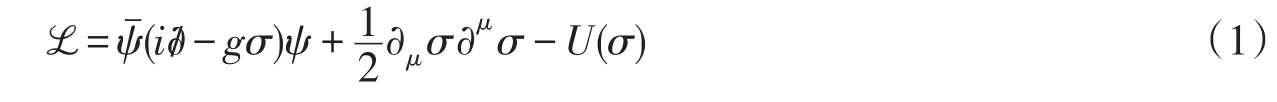
它描述了自旋1/2的夸克场ψ与唯象标量场σ以及它们的相互作用，g是耦合常数.低能条件下σ场唯象的描述了胶子的作用，U(σ)是一种经典势表征由于色场的非线性相互作用导致的真空凝聚.本文中将只讨论u夸克和d夸克的情况.σ场的经典势形式取为

模型中的参数ɑ,b,c和g可调，在一组固定的ɑ,b,c参数下，则U(σ)在σ0=0时有一个局域最小值，在σ=συ时有绝对最小值，συ由U（σ）的一阶导数为零得到

σ0代表的亚稳态真空，συ代表物理真空或非微扰真空，两个真空状态的势能差定义为袋常数B.如果我们取U(συ)=0，袋常数可表达为B=-(/2!+/3!+/4!).

应用欧拉-拉格朗日方程，从（1）式可得到对应的方程

在平均场近似下，σ场是不随时间变化的经典场，并且是球对称的.组分夸克位于最低的s波能级，σ场和ψ场可以写成以下形式

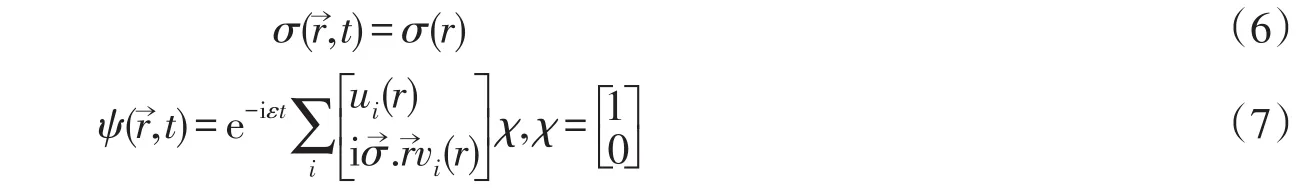
应用等式（4）～（7），可以推导出关于u，v，σ的微分方程

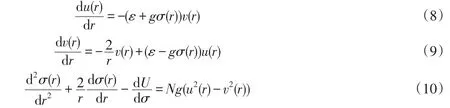
归一化条件为4π∫r2(u2(r)+v2(r))dr=1，满足的边界条件为v(0)=0=0,u(∞)=0,σ(∞)=σv.方程组边界条件选取的物理考虑如下：v(r)是狄拉克旋量解的P波部分，所以v(0)=0，另外在方程（9）中存在v(r)/r的项，r=0处方程组有解也要求v(0)=0；同样从解方程的角度，方程（10）中存在r的项，所以=0；强子是一种束缚态，u(r)在无穷处的值为0，所以u(∞)=0；强子外是物理真空，物理真空的σ期望值是σv，所以σ(∞)=σv.

夸克数N=3对应重子，N=2对应介子.由于方程组高度非线性，无法解析求解，可以用数值方法通过一套基于colsys的程序集解得，在MATLAB、Scilab中可以方便的得到数值结果.在文献［3］中用了很多参数计算强子性质，我们取的参数为ɑ=17.70 fm-2,b=-1 457.4 fm-1,c=2 000,g=12.16.在零温度零密度下，我们得到的孤子解如图1所示，孤子解与Wilets文中的结果一致［2］，σ场阶跃式的位形确保了夸克的囚禁.

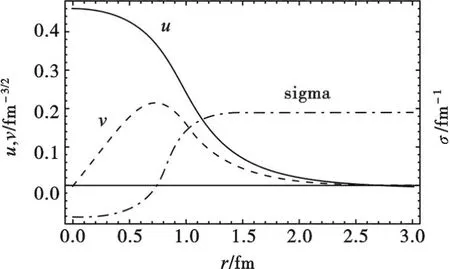
图1 零温度零密度下的孤子解

2 退禁闭相变

在有限温度密度下，也就是重离子碰撞产生的热密环境中，σ场的经典势不再适用，考虑温度密度效应经典势要替换为有效势V（σ，β，μ）.应用温度场论引进温度密度效应，使用Dolan和Jackiw的方法［9］，在有限温度密度下FL模型的有效势计算如下.

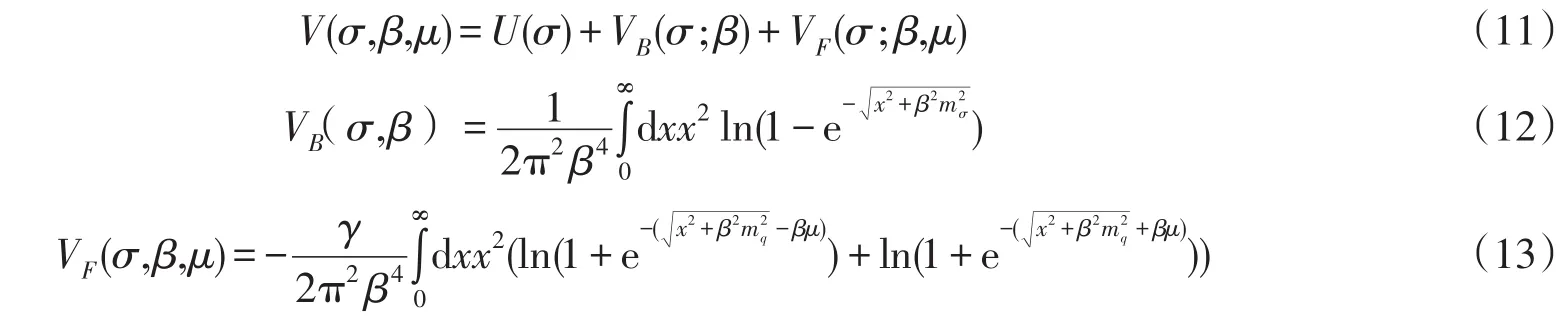
VB和VF为玻色子和费米子在有限温度密度下对有效势的贡献.x是无量纲的积分变量.β为T的倒数，mq与mσ分别为夸克场与σ场的有效质量，其形式为mq=gσ，mσ=ɑ+bσ+cσ2/2.γ是自由度简并因子，它包含了夸克的自旋、味道和颜色的自由度，即：γ=2(自旋)×2(味道)×3(颜色)=12.

在给定温度密度下，V(σ,β,μ)只是σ的函数，应用数值方法可得到有限温度密度下的有效势图.图2为零密下不同温度时有效势的变化情形，随着温度升高，强子外部物理真空对应的热力学有效势极值不断上升，若固定物理真空有效势极值为零则表现为强子内部微扰真空有效势极值逐步降低，当两个真空对应的有效势极值相等时，退禁闭相变发生.B为强子内外两个真空的势能差，即袋常数，通过B=0寻找相变临界点，而

从图2可以看到，在一定化学势下随着温度的升高，固定强子外部物理真空有效势为零时强子内的亚稳态真空势能降低，慢慢接近物理真空势能，在给定温度下随着化学势的升高，有效势的变化也是类似的.由热力学势变化确定临界点，给定μc=60 MeV，通过B=0可以找到Tc=116.4 MeV的临界点，同样给定Tc=10 MeV，也可以找到μc=295.5 MeV的临界点.由此，我们可以找到不同温度和密度下的退禁闭相变点（Tc,μc），图3是计算156个点给出的退禁闭相图.

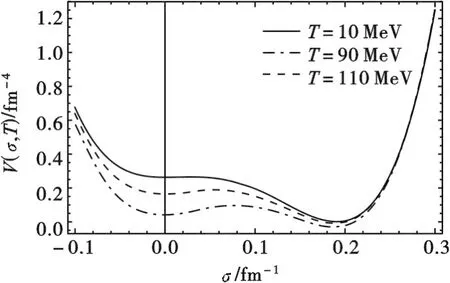
图2 零密度不同温度下的有效势

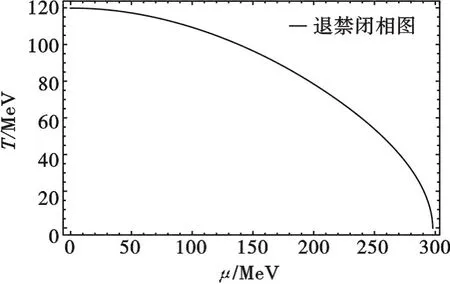
图3 有限温度密度下的退禁闭相图

3 有限温度密度下孤子的变化

得到有限温度密度下的有效势后，在实际孤子方程的计算中可将V(σ)用数值方法拟合成关于σ的幂级数形式，仍取σ2、σ3、σ4的形式，这些项起主要作用.在固定温度密度值下，可得到一组ɑ,b,c参数值，所以有限温度密度下的有效势可表示为

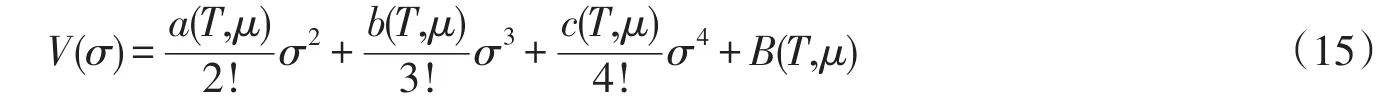
将（15）式替换（10）式中的U(σ)便得到有限温度密度下的孤子方程组，采用与零温零密下类似的方法可得到不同温度密度下的孤子解.图4给出了零密下不同温度时的孤子解，u、v随温度升高幅度变小宽度变宽，u、v、σ的位形均向右移动，反应了夸克活动范围的扩展.在相边界附近，孤子解会突然消失，这说明孤子在相变区域发生了解体.

如果考虑最低能量状态下的N个夸克，体系的总能量为

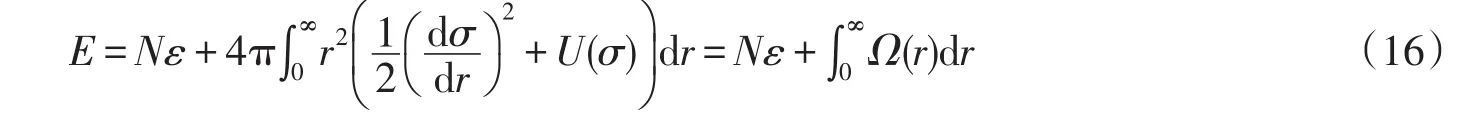
孤子在空间的能量分布可由能量密度Ω(r)展现出来，如图5所示.由图5可以看出，随着温度的升高，孤子能量密度位形分布宽度变宽且幅度变小，并且整体向右迁移，这说明空间局域的能量分布在逐渐由中心向外围延展.在相变附近，孤子能量波包突然坍塌，孤子能量只剩下作准自由运动的夸克的能量.这与退禁闭相变的物理图景是一致的.在重离子碰撞实验中，重核碰撞产生高温高密的极端条件下发生退禁闭相变，这时重子挤压在一起重子袋破裂，夸克束缚解除，解禁闭的夸克可以在火球内准自由运动.

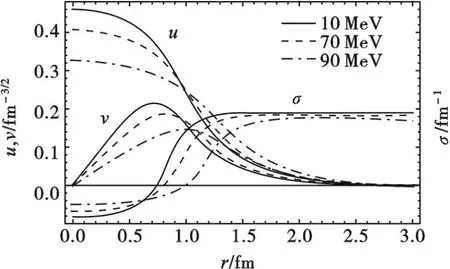
图4 零密度不同温度下的孤子解

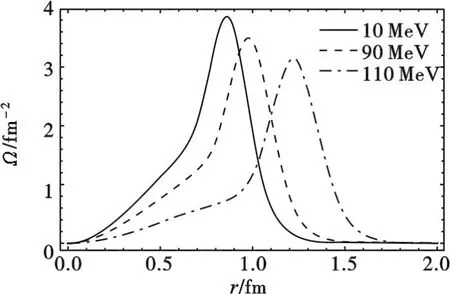
图5 能量的空间位形分布

4 结论

研究表明，在有限温度密度下固定化学势当T＜Tc（或固定温度当μ＜μc）时，始终存在非零的袋常数，微分方程组始终有稳定的孤子解.然而，当T＞Tc（或μ＞μc）时，袋常数等于零，孤子解消失，空间局域的能量分布消失，夸克可以作准自由运动，退禁闭相变发生.孤子的变化与退禁闭相变是一致的.值得注意的是在我们的计算中还发现在相变临界点孤子解并不会立即消失，而是在过了临界点一定范围后，孤子解才消失.这说明退禁闭相变后还存在着短暂的夸克束缚态，这可能和高能重离子碰撞实验中产生的强耦合QGP有关，这是一个有趣的现象，值得以后作进一步深入研究.

［1］Friedberg R，Lee T D.Fermion-field nontopological solitons［J］.Physical Review D，1977，15（6）:1694-1711.

［2］Wilets L.Nontopological solitons［M］.Singapore:World Scientific，1989.

［3］Goldflam R，Wilets L.Soliton bag model［J］.Physical Review D，1982，25（7）:1951-1963.

［4］高道国.孤粒子袋模型的数值解法［J］.四川大学学报：自然科学版，1990（2）:190-196.

［5］Shu S，Li J R.Describing the strongly interacting quark-gluon plasma through the Friedberg-Lee model［J］.Physical Review C，2010，82（4）:0452031-0452035.

［6］Shu S，Li J R.The vacuum tunnelling and the crossover of deconfinement in Friedberg-Lee model［J］.Nuclear Physics A，2013，901:1-13.

［7］Mao H，Yao M，Zhao W Q.Friedberg-Lee model at finite temperature and density［J］.Physical Review C，2008，77（6）: 0652051-0652059.

［8］Kapusta J I，Gale C.Finite-temperature field theory:principles and applications［M］.Cambridge:Cambridge University Press，2006.

［9］Dolan L，Jackiw R.Symmetry behavior at finite temperature［J］.Physical Review D，1974，9（12）:3320-3341.

（责任编辑 郭定和）

Research on deconfinement phase transition and the properties of soliton

DONG Renda，SHU Song，ZHANG Hui
（School of Physics and Electronic Science，Hubei University，Wuhan 430062，China）

The FL model is studied at finite temperature and density，the effective potential has been calculated at different temperatures and densities by using the technique of the finite temperature field theory. Deconfinement phase transition takes place in FL model when the effective potentials inside and outside hadron are equal.The phase diagram of deconfinement is obtained by calculating critical points carefully.It turns out that there are always stable soliton solutions in hadronic phase and soliton solutions vanish after deconfinement phase transition.The variation of solition is consistent with the deconfinement phase transition.

deconfinement phase transition；friedberg-lee model；soliton；finite temperature field theory

O572.24+6

A

10.3969/j.issn.1000-2375.2015.05.009

1000-2375（2015）05-0447-04

2014-11-26

国家自然科学基金（10905018）资助

董仁达（1990-），男，硕士生；通信作者，舒崧，副教授，E-mail:shus@hubu.edu.cn