一般状态空间马氏过程随机泛函的指数矩

屈 聪，张水利，田 菲

(1.平顶山学院数学与信息科学学院，河南平顶山467000；2.空军预警学院黄陂士官学校基础部，湖北武汉430019)

一般状态空间马氏过程随机泛函的指数矩

屈 聪1，张水利1，田 菲2

(1.平顶山学院数学与信息科学学院，河南平顶山467000；2.空军预警学院黄陂士官学校基础部，湖北武汉430019)

研究一般状态空间马氏过程随机泛函的指数矩，利用最小非负解理论，得到随机泛函的指数矩是相应方程的最小非负解，并利用此结论证明矩条件与漂移条件等价.①

马氏过程；随机泛函；指数矩；最小非负解

0 引言

马氏过程泛函的矩已有许多学者进行了研究，王梓坤［1］研究了连续时间可数状态空间马氏链(即Q过程)的随机积分型泛函的矩；李俊平等［2］研究了Markov骨架过程随机积分型泛函的分布与矩；来向荣［3］研究了非齐次生灭过程的积分型泛函；陈柳鑫等［4］研究了非齐次(H,Q)过程随机积分型泛函的分布与矩；唐有荣等［5］研究了半马氏过程的随机积分型泛函的矩.而笔者利用文献［6］中有关最小非负解一般理论，研究了一般状态空间马氏过程随机泛函的指数矩.

设(E,ξ)是局部紧可分度量空间，{Xt,t∈R+}是(E,ξ)上轨道右连续的马氏过程，转移概率函数为{P(t,x,A):t∈R+,x∈E,A∈ξ}(相应半群是{Pt}).对任意的A∈ξ，常数δ＞0,记

τA(δ)表示马氏过程在时间δ后，首次到达集合A的时刻.

条件C0：存在一个非空集合C，常数δ＞0,满足Xt∉C,∀t∈(δ,2δ].

1 主要结果

定理1.1设{Xt,t∈R+}是(E,ξ)上满足条件C0的马氏过程，常数λ＞0,函数f:E→[0,∞)，则随机泛函的指数矩dt],x∈E}是方程

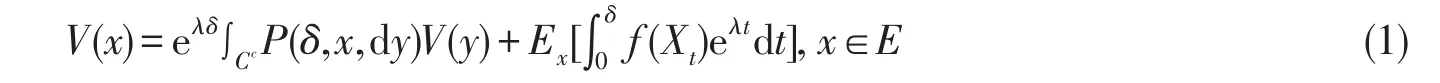
的最小非负解.

的最小非负解.

定理1.3设{Xt,t∈R+}是(E,ξ)上满足条件C0的马氏过程，常数λ＞0,且(Xt)eλtdt]＜∞,则下列两个条件等价

(i)漂移条件:存在非负函数V，满足方程

2 定义及引理

令ℋ表示从E到Rˉ+上的映射集合:ℋ包含1，且对非负线性组合及单调递增极限封闭，则ℋ是一个凸锥.称A是从ℋ到ℋ的一个锥射，若A0=0,

令ℒ:={A:ℋ→ℋ,A是一个锥射，当fn∈ℋ,fn↑f⇒Afn↑Af}.

定义2.1[6]给定A∈ℒ,g∈ℋ,称f∗为方程刊

的最小非负解，若f∗满足(3)式且对于任何满足(3)式的f˜∈ℋ，都有

引理2.2[6]方程(3)的最小非负解一定存在并且唯一.进一步，最小非负解可以通过下面递推方法构造:令

则当n→∞时，f(n)↑f∗.

引理2.3[6](局部化定理)设U是一个非负可测核，{f∗(x),x∈E}是方程

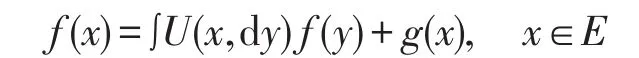
的最小非负解，令G⊂E且{f˜∗(x),x∈G}是方程

的最小非负解，则我们有

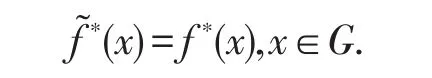
引理2.4[6](比较定理)设A,A˜∈ℒ，g,g˜∈ℋ，满足A˜≥A，g˜≥g，f∗是方程(3)的最小非负解，则方程

的任意解f˜，都有f˜≥f∗.

令

引理2.5设条件C0成立，则对任意的x∈E,有

引理2.5的证明当n=1时，τ(1)C(δ)=min{τC(δ),δ}=δ，所以

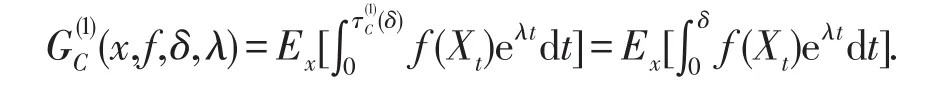
用θ表示通常的漂移算子，注意到，在条件C0成立的条件下，当τC(δ)＞δ时，有

3 主要结果的证明

定理1.1的证明令

下面利用归纳法证明，对任意的n≥1,x∈E,都有

当n=1时，由(4)式，有

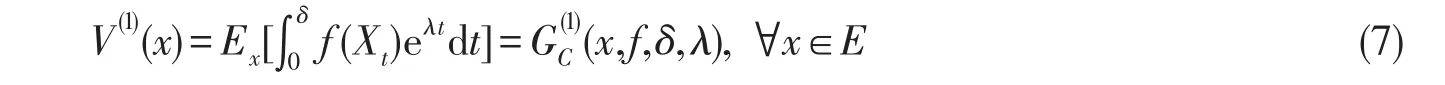
即n=1时，(6)式成立.

假设n=k＞1时，(6)式成立，即V(k)(x)=(x,f,δ,λ).由(5)式，有

即n=k+1时，(6)式仍成立.由引理2.2可知，方程(1)的最小非负解为:

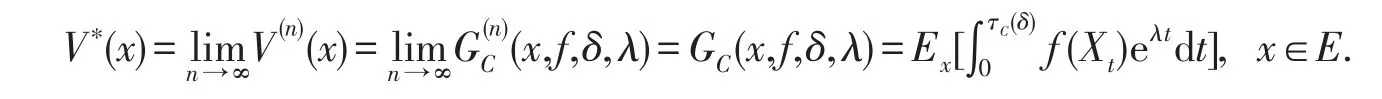
推论1.2的证明由定理1.1及局部化定理(引理2.3)可知结论成立.

定理1.3的证明(i)⇒(ii)，令

由推论1.2及引理2.4可知，{V˜(x),x∈E}是方程(2)的最小非负解.由条件(i)成立，有

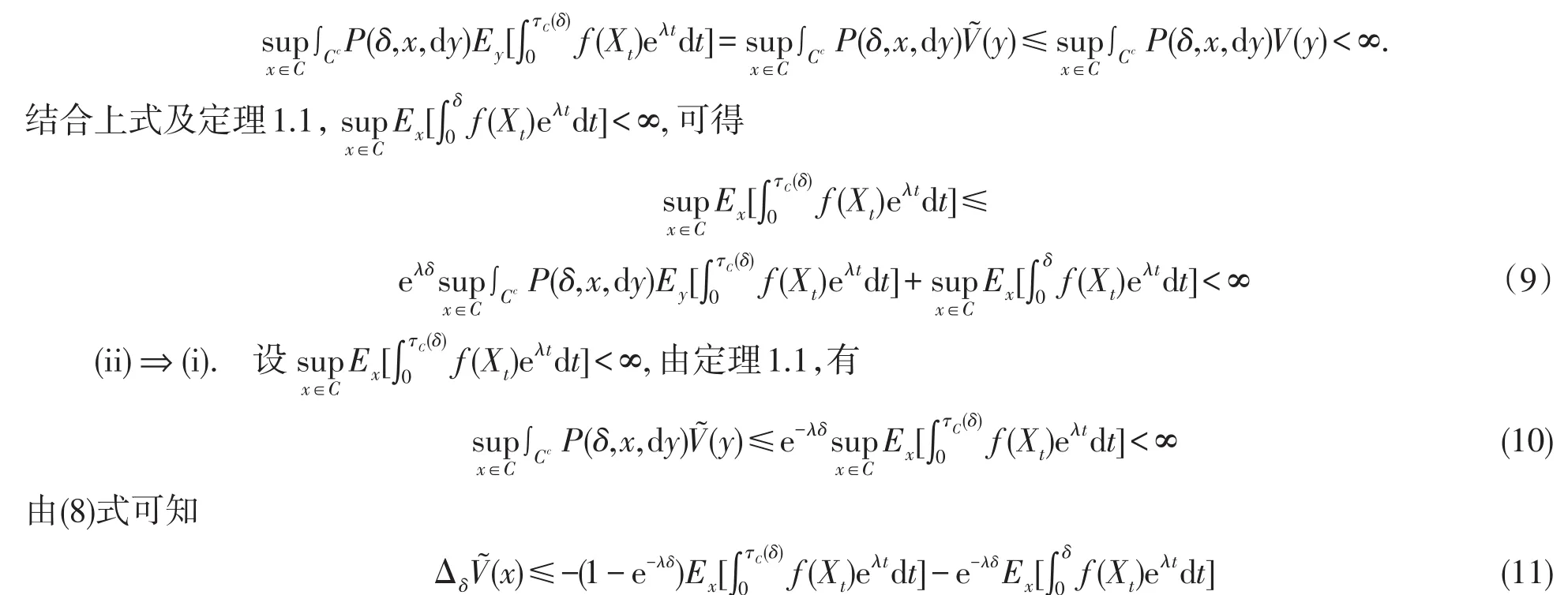
由(10)-(11)式可知，非负函数{V˜(x),x∈E}满足方程(2).

［1］王梓坤.生灭过程与马尔可夫链［M］.2版.北京:科学出版社，2004.

［2］李俊平，侯振挺.Markov骨架过程积分型泛函的分布与矩及其应用举例［J］.应用数学学报，2001，24(2):277-283.

［3］来向荣.非齐次生灭过程的积分型泛函［J］.工程数学学报，1994，11(2):69-75.

［4］陈柳鑫，李俊平，侯振挺.非齐次(H,Q)过程的积分型泛函的分布与矩［J］.长沙铁道学院学报，2000，18(3):81-85.

［5］唐有荣，刘在明，侯振挺.半马氏过程的积分型随机泛函［J］.数学年刊，1999，20 A(5):553-558.

［6］Chen Mufa.From markov chains to non-equilibrium particle systems［M］.second edition.Singapore:World Scientific，2004.

（责任编辑 赵 燕）

The exponential moments of stochastic functional for Markov processes on general state space

QU Cong1，ZHANG Shuili1，TIAN Fei2
(1.School of Mathematics and Information Science，Pingdingshan University，Pingdingshan 467000，China；2.Department of Basics，Huangpi NCO School，Air Force Early Warning Academy，Wuhan 430345，China)

The exponential moments of stochastic functional for Markov processes on general state space was studied，we obtained the minimal nonnegative solutions to the corresponding equation was the exponential moments of stochastic functional，by using the theory of minimal nonnegative solutions.As applications，the equivalent between the moment condition and the drift condition are proved.

Markov processes；stochastic functional；exponential moment；minimal nonnegative solutions

O211.62

A

10.3969/j.issn.1000-2375.2015.05.007

1000-2375（2015）05-0438-04

2015-02-10

河南省教育厅科学技术研究重点项目(14B110038)资助.

屈聪(1981-)，女，硕士，讲师；张水利，通信作者，讲师，E-mail：zhangshuilicong@126.com