球形光电成像跟踪转台的螺旋式扫描及控制方法*

雍爱霞，吴微露

（电子工程学院，合肥 230037）

球形光电成像跟踪转台的螺旋式扫描及控制方法*

雍爱霞，吴微露

（电子工程学院，合肥 230037）

采用球形电机作为光电成像跟踪转台的旋转机构，研究一种新型高集成度和超大视场的光电成像跟踪系统。针对球形转台的特殊结构和旋转特点，分析了转台在三维空间中进行螺旋式扫描的特性，并设计了相应的控制方法，采用实四元数组作为转台旋转控制的数据结构。仿真结果表明，球形转台可以按预先设置的参数进行旋转，避免了空间的漏扫。

球形转台，螺旋式扫描，四元数

0 引言

目前国内光电成像跟踪系统的类型主要有地平式光电跟踪系统、X-Y式光电跟踪系统、空间CCD凝视成像跟踪系统等，在结构和性能上它们各有特色［1-2］。从运动学角度来看，三维空间旋转以球形结构的电机最为有利，它可以实现多自由度的旋转与定位，这对于提高光电侦察设备的高集成度和视场范围有着重要的影响。球形光电成像跟踪转台模型如图1所示，目前国内尚没有相关文献，英国1989年服役的“海射手30型光电火控系统”结构外观呈球形，是当时世界上最先进的火控系统之一；美国1989年研制的MMS光电跟踪仪采用的是轻小球形结构跟踪座，在海湾战争中被装在许多战舰和航空装备中，并执行大视场夜间导航等多项特殊任务；以色列研制的MSIS多传感器光电火控系统具有球形头部结构，不仅可以用于机载、星载等成像跟踪测量系统，还可以用于中小型战舰上桅杆载巡逻侦察成像监测系统［3］，但这些设备所采用的机械结构和伺服控制系统都没有文献记载。

图1 新型球形光电成像跟踪系统

图2 永磁球形电机模型

本文采用球形电机对跟踪系统的机械结构进行优化，如上页图2所示，它的电机模型结构采用美国Hopkins大学设计的永磁球形步进电机原型机［4-5］，球形电动机的发展可以追溯到50年代，但受技术条件的限制，在较长时期内进展缓慢，目前国内外对球形电机已完成基础理论及其控制策略的研究，它的研制开发具有广泛的应用前景。

1 球形转台空间的螺旋式扫描

1.1 球形转台的扫描特性

按照球形电机结构和运动的特殊性，转台的螺旋式扫描将球面空间按转台边缘周线划分为若干个瞬时视场的集合，经过连续等间隔的采样，浓缩在监视器上凝视显示，如果位标器为调制盘系统或十字叉系统，则瞬时视场为圆形，如图3所示，若每个圆心为视轴所能到达的位置，那么搜索视场是相当可观的。

图3 瞬时视场示意图

图4 重叠部分示意图

为防止搜索视场内出现漏扫的空域，通常要求相邻瞬时视场间有适当的重叠，重叠系数k定义为相邻瞬时视场间的重叠部分δ与瞬时视场2r之比，即k=δ/2r。通常要选取适当的重叠系数，以确保一定的发现概率［6］，图4中θ（δ）为重叠部分对应的球心角，θ’为两相邻视轴对应的球心角。

其中，D为球体半径，h为探测器相比于球面的高度，则两相邻视轴对应的球心角为：

1.2 螺旋式扫描的运动轨迹

转台的三维视场近似看成是球体空间，如球面位置分割成图3所示若干瞬时视场的集合，则空间扫描基本上可以消除盲区。设定重叠系数δ=0，视轴的空间转动轨迹将球面划分为若干圆形，如图4所示，由球形步进电机实现的螺旋式扫描可以分为两个步骤来完成：

图5 视轴扫描轨迹的俯视图

图6 视轴扫描运动的正视图

（1）视轴绕Z轴即轴向量（0，0，D）作圆周扫描

θ为两相邻视轴对应的圆心角，忽略弧线误差，两视轴的直线距离等于2r，如图6所示，视轴从内而外第n外圈函数的运动轨迹为：

（2）相邻圆周扫描间的跃迁

完成圆周扫描线间的阶跃将会有很多运动轨迹，这里采用就近原则，已知第i外圈：

其中，（x0，y0），寻找第i+1外圈的（x'0，y'0），必须满足条件：

①距离最近；

②必定沿着过球心的最大外圈旋转，则法线向量Vn1满足：

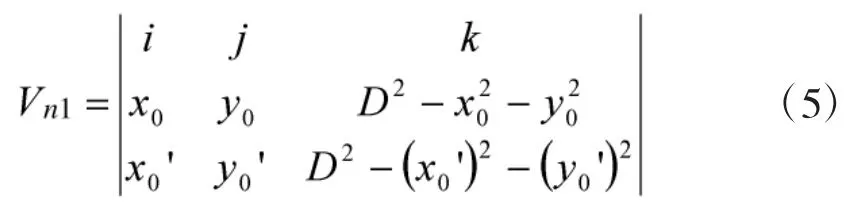
2 球形转台螺旋式扫描的控制方法

2.1 球形驱动电机的步进旋转

作为转台的执行机构，球形电机复杂的电磁场和矩角特性表明了线圈通电、换相的条件［7-9］，为简便计算，本文只讨论两个线圈同时通电的旋转情况，定子结构如图7所示［4-5］，定子与永磁体初始位置如图8所示。

图7 定子线圈的结构

图8 定子与初始位置下的永磁体

令此时Wm、Wn号线圈附近有两个距离相等的永磁体对Mi、Mj，且符合路径要求，给线圈对Wm、Wn通电从产生相应的转动，其旋转轴线向量和旋转角度分两步来计算［10］。

第一步旋转四元数的哈密尔顿表示为：

第二步旋转以线圈Wm（即Mi旋转后的新坐标）为轴线，Wn通电吸附永磁体Mj，其中Mj经由第一步旋转后的新坐标Mj'。

该四元数的哈密尔顿表示为：

则定子线圈换相的旋转角度与转轴向量分别为：

2.2 基于四元数组加权有向图的控制方法

由球形电机的各步进旋转构造一个加权有向图，如图9所示，用G=（V，E，D）表示，节点V表示为一个数组（Mi，Mj，Wm，Wn），为满足通电条件的线圈对和永磁体对，E为V上顶点的无序对（Vi，Vj），表示一次步进旋转。权值D是一个四元数组，为转子由当前节点转动到下一节点时，由式（6）到式（8）计算出相应的旋转四元数。

图9 各次步进旋转的加权有向图

由于步进电机多次旋转的误差为累积误差，令R1、R2……为各次序旋转的四元数，R1-1、R2-1……分别为各四元数的逆，则组合旋转的四元数表示为：

由于螺旋式扫描存在重叠系数，为了避免扫描过程的漏扫和多扫，设置合适的δ，使得累积误差Δθ＜θ，θ为δ对应的圆心角。

当Δθ＞θ时，需要进行一次误差补偿，即重新寻找一次旋转路径，使得：

基于四元数组加权有向图的控制方法如下：

①按式（9）计算符合预定轴线向量的第i条路径，并放入线圈通电次序表中；

②如果i=n，则结束退出，否则计算符合预定轴线的第i条路径，同时按式（10）计算前i次组合旋转的四元数组；

③按式（11）计算前i次的累积误差，如果Δθ＞θ，重新计算符合式（12）的第i条路径；

④将第i条路径放入线圈通电次序表中，i=i+1，转步骤②。

3 仿真分析

设置D=1、k=0.5，即θ（δ）=θ’，假定瞬时视场r=0.2D，计算出此时重叠部分δ=0.2，θ（δ）=23°。输出轴从初始位置（0，0，1）处跃迁到第一外圈的相邻位置，预定转轴为（0.707 11，0.707 11，0），预定转角为23°。按步进旋转的加权有向图需要两步完成，Step1各永磁体和线圈位置如下页图10所示，Step2各永磁体和线圈位置如图11所示，各步进的旋转要素与预定旋转要素之间的对照见表1所示。

图10 Step1各永磁体和线圈的位置

图11 Step2各永磁体和线圈的位置

由表1各旋转要素可知，加权有向图中各次旋转是有限的，预定旋转实际由两个步进旋转来等效，等效的四元数组为［0.980 79 0.151 77 0.121 59 0.014 633］，其中Step2旋转向量与预定旋转向量的误差为0.133 0 rad，输出轴初始位置坐标经预定旋转后为（0.242 95 -0.294 15 0.924 35），实际旋转后坐标为（0.259 4 -0.284 86 0.922 61），各坐标方向误差均小于0.01个单位。

表1 预定旋转与实际旋转的对照表

表2 Step2旋转要素及输出轴坐标

各外圈的圆周扫描运动皆是以（0，0，1）为旋转的预定轴线，根据图9的步进加权有向图，计算出Step1实际旋转轴线为（0.107 32，0.307 47，0.945 49），旋转角度为0.431 61 rad，与预定轴线的误差为Δθ=0.331 7 rad。可以进行一次误差校正，即在后续的各次旋转中计算寻找出Step2，使得两次组合旋转的Δθ为最小，各次旋转的旋转要素和输出轴坐标如表2所示。

从表2中各次旋转的四元数组数据进行计算，其中n=1步进旋转对应的旋转轴线为（0，0.175 48，0.98448），与预定轴线（0，0，1）误差角为0.174 61 rad，然而与圆周扫描Step1组合旋转的误差属于累积误差，累积误差为0.284 63 rad，该误差已小于Δθ；n=6步进旋转对应的旋转轴线为（0.10263，-0.98478，0.140 28），与预定轴线误差角为1.430 1 rad，与Step1组合旋转的累积误差为0.090 024 rad，所以可以用来进行一次误差校正。

4 结论

本文采用球形电机作为转台的主要执行机构，解决大视场和高机械集成度的问题，研究转台在三维空间螺旋式扫描的特性参数和控制方法，仿真从螺旋式扫描的两个步骤出发，表明转台可以按预定轴线旋转，个别步距角较大并存在累积误差，需要选择合理的重叠系数，例如本文取k=0.5，可以避免空域的漏扫，后续工作中可以适当减小重叠系数，以提高搜索频率和发现概率。

［1］刘兴法，马佳光，苏赋.三轴光电跟踪系统的实时引导［J］.光电工程，2006，33（12）:1-4.

［2］姬伟，李奇，杨海峰，等.精密光电跟踪转台的设计与伺服控制［J］.光电工程，2006，33（3）:11-16.

［3］王毅，于前洋.轻小球型光电跟踪仪［J］.光机电信息，1997，14（10）:12-14.

［4］Gregory S C，David S.Kinematic Design and Commutation of a Spherical Stepper Motor［J］.IEEE/ASME Transactions on Mechatronics，1999，4（4）：342-353.

［5］David S，Edward R S，Gregory S C.Mathematical Models of Binary Spherical-Motion Encoders［J］.IEEE/ASME Transactions on Mechatronics，2003，8（2）:234-244.

［6］高稚允，高岳，张开华.光电成像技术系列教材——军用光电系统［M］.北京：北京理工大学出版社，2008.

［7］王群京，李争，夏鲲，等.新型永磁球形步进电动机结构参数及转矩特性的计算与分析［J］.中国电机工程学报，2004，24（9）：192-197.

［8］吴立建，王群京，杜世俊，等.磁场积分法在永磁步进球形电动机场分析中的应用［J］.中国电机工程学报，2006，26（10）：158-165.

［9］Wang Q G，Zheng Li.Magnetic Field Computation of a PM Spherical Stepper Motor Using Integral Equation Method［J］. IEEE Trans.on Magnetics，2006，42（4）:731-734.

［10］雍爱霞，王群京，倪有源.基于四元数组的球形永磁步进电机控制研究［J］.微电机，2006，39（9）：33-37.

Helical San and Control Method for Turntable of the Spherical Opto-electronic Imaging Tracking System

YONG Ai-xia，WU Wei-lu
（Electronics Engineering Institute，Hefei 230037，China）

Spherical motor is used for the rotatable part of the opto-electronic imaging tracking turntable in this paper，a new kind of opto-electronic imaging tracking system which has high integration and especially wide field of view is studied.Due to the special structure and rotating trait，the helical scan character of the turntable in the three-dimensional space is analyzed，and the corresponding control method is designed，meanwhile quaternion is used for the data structure of the turntable rotation.Simulation result shows that the spherical turntable could rotate according to the parameters which are set in advance，thus avoiding the missing scan in the space.

spherical turntable，helical scan，quaternion

TM35

A

1002-0640（2015）04-0023-04

2014-03-25

2014-04-27

中国博士后科学基金资助项目（20090461419）

雍爱霞（1974- ），女，安徽定远人，博士后。研究方向：新型光电成像跟踪系统、特殊信号处理技术。