基于GERT的武器装备维修备件订货间隔期预测*

邵延君，马春茂，潘宏侠，刘永姜

（1.中北大学机械与动力工程学院，太原 030051；2.西北机电工程研究所，陕西 咸阳 712099）

基于GERT的武器装备维修备件订货间隔期预测*

邵延君1，马春茂2，潘宏侠1，刘永姜1

（1.中北大学机械与动力工程学院，太原 030051；2.西北机电工程研究所，陕西 咸阳 712099）

由于武器装备维修备件的需求是随机波动的，订货间隔期的准确预测就成为了一个难点。针对这样一个随机波动的需求系统，提出了利用GERT随机网络模型对其进行描述，进而求出随机波动需求的订货间隔期的解析表达式，解决了不确定性需求的订货间隔期的预测问题，为武器装备维修备件的科学管理提供数据支持。通过实例验证表明，GERT随机网络模型是解决武器装备维修备件订货间隔期的一种有效手段和方法。

GERT模型，随机波动，订货间隔期，维修备件

0 引言

由于武器装备维修备件的需求是一种随机需求，因此，备件的订货周期也是一种随机过程，这就给维修备件的采购工作带来了很大的困难。合理的订货间隔期预测可以提高资金的使用效率，同时可以有效防止资金储备不足而影响备件的采购工作，进而影响装备的维修和使用。迄今为止，根据订货点和订购量选择方式的不同，随机需求的订货策略存在4种模型，这4种随机订货策略都是在周期性检查或者连续检查库存水平的情况下来进行订货的［1-3］，根据库存水平的盘点来决定订货时间的策略是无法做到对订货间隔期进行预测的。目前，对于武器装备维修备件这种随机波动需求的订货间隔期的预测还缺少有效的工具，基于以上原因，考虑利用 GERT（Graphical Evaluation Review Technique）随机网络模型对随机波动需求订货间隔期进行预测。

GERT是一种融合了概率论的矩母函数和控制论中的信号流图等多种理论和方法的技术，该技术又被称为评审技术，是一种针对随机变化环境条件下对系统的一种网络描述［4-5］。目前，它已被广泛的应用在产品回收、再制造、灾害演化等很多方面［6-8］。本文建立GERT随机网络装备维修备件的订货间隔期仿真模型，来预测随机需求下的订货间隔期，该模型能将维修备件的随机需求转化为形象直观的网络图，并通过参数的计算来预测维修备件的订货间隔期，对部队的维修和采购工作具有现实的指导意义。

1 GERT随机网络模型的解析算法原理

1.1 矩母函数

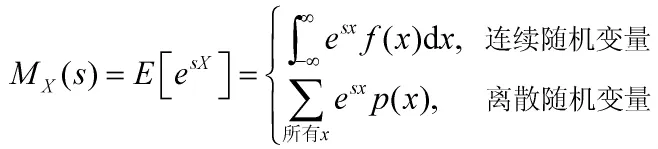
式中：X为随机变量；s为任意的实数；MX（s）为随机变量X的矩母函数。

1.2 信号流图的梅森拓朴方程

式中：Tij为表示节点i到节点j的等价传递系数；xi，xj为表示任意两个节点的变量值；

△为表示信号流图的特征式；pk为表示第k条路径上的传递系数；

△k为表示消去第k条路径后的剩余子图的特征式。

同时：△=1-∑T（L1）+∑T（L2）-∑T（L3）+…=1-∑奇阶环的传递系数+∑偶阶环的传递系数。

1.3 GERT随机网络的传递函数

令f（tij）为活动（ij）这个随机变量的条件概率密度函数，则得到条件矩母函数为：

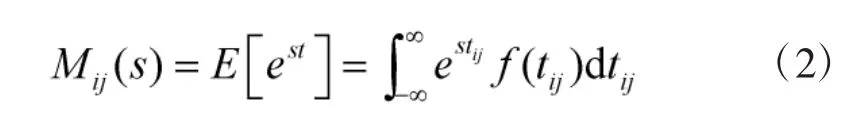
定义Wij（s）为活动（ij）的传递函数，则：

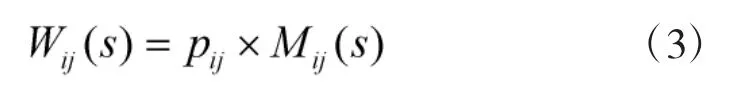
pij为节点i实现时，活动（ij）被执行的概率。

1.4 GERT随机网络的求解步骤

①求解Wij（s）这个网络函数的等效函数WE（s），则：

②求解网络的等价参数PE；

概率PE就等于等价传递函数WE（s）在s=0时的值

即：

③根据等效函数WE（s）和网络的等价参数PE以及矩母函数的性质来求解网络的等价参数TE；

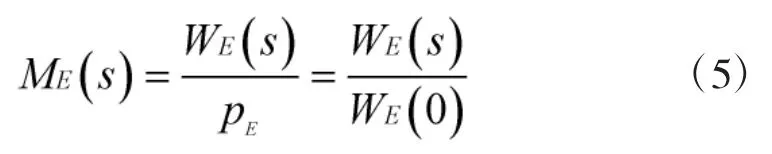
矩母函数的n阶导数在s=0处的数值，是随机变量的n阶原点矩：

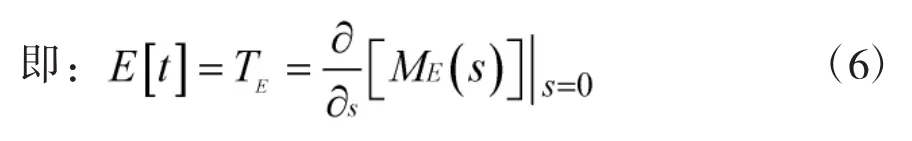
由此可知，GERT网络模型使矩母函数和信号流图原理在GERT网络中结合起来，可以求出任意两个节点之间的WE（s）以及PE和TE等参数。GERT解析算法巧妙的运用了矩母函数的反演特性，为我们提供了求解随机网络的工具。

2 基于GERT网络模型的订货间隔期的实例分析

根据XX雷达维修所的库存系统的数据资料，对于XX价格比较昂贵的维修备件，维修所每周对备件的库存量进行一次盘点，当发现备件的库存为0时，则立刻进行订货，使库存的存贮量恢复到正常水平，假设正常的存贮水平是3件，维修部门每隔3周来提取一次备件，每次提货数量的概率分别为P（0）=0.5，P（1）=0.4，P（2）=0.1。

2.1 建立GERT网络模型

把备件的存贮量水平0、1、2、3看作是GERT网络的4个状态，在4个状态的基础上再增加1个状态-l，表示因库存缺货而等待的状态，这样，整个的GERT网络就包括了5种状态。从0和-1节点返回3节点的活动表示订货及到货的情况，即刻到货表示到货的时间为零，由于到货的时间为零，所以从-1和0节点到3节点的时间为t=0，根据式（2），得到矩母函数Mij（s）=1；概率Pij=1，传递函数Mij（s）=1。

再根据式（2），求其余各节点间的矩母函数，当提货的时间间隔为3周时，则其余各节点间的矩母函数为：

根据式（3）可以得到节点之间的传递函数为：

根据各个节点传递的概率和所求的矩母函数，可以得到GERT网络模型如下页图1所示。

2.2 求两次订货的时间间隔

为了确定两次订货之间的时间间隔，将GERT网络中引向节点3的订货活动移到虚节点3'，如图2所示，各个节点之间的传递函数没有变化。

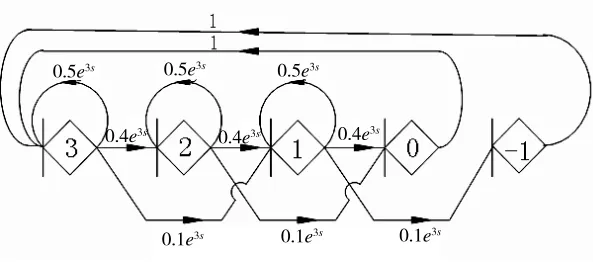
图1 GERT网络模型图

图2 构建虚节点后的GERT网络模型图

首先来求梅森的拓朴方程里面的参数：

①信号流图的特征式△为：

②第k条路径上剩余子图的特征式的乘积的和为：

然后根据式（1）则可以得到3到3'的传递函数为：

根据式（4）可以得到3到3'的PE的值为：

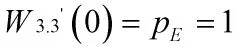
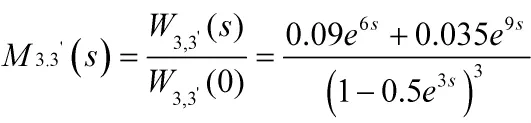
根据式（6），对矩母函数求导，令s＝0，则可以得到两次订货的时间间隔期TE为：

根据雷达维修所的订货的统计数据表明，平均每次的订货间隔期恰好是16周，但是如果提货的每次提货数量的概率和周期发生变化的时候，订货间隔期也会随着变化，可继续利用GERT随机网络的解析算法得到随机波动需求的订货间隔期。可证明GERT随机网络的解析算法是解决随机波动需求的订货间隔期的一种有效工具。

3 结论

GERT网络丰富的箭线参数和节点能够对系统的状态进行恰当的描述，并能将各个状态之间的复杂的转移过程转化为直观形象的网络模型，利用信号流图的梅森方程和矩母函数的性质，对整个存贮系统GERT网络模型运用相应的解析算法，进而求出解析表达式，可以得到维修备件随机波动需求下的订货间隔期等指标，这些指标能为科学管理装备维修备件的仓库，以及合理安排备件订货等提供数据支持。

［1］汤雅青.非平稳随机需求库存控制模型研究［D］.上海:上海交通大学，2011.

［2］杨杰.非平稳需求库存控制策略研究［D］.合肥:中国科学技术大学，2007.

［3］王慧枝.非平稳需求条件下备件库存控制方法研究［D］.沈阳:东北大学，2008.

［4］冯允成，吕春莲.随机网络及其应用［M］.北京:北京航空航天大学出版社，1987.

［5］Pritsker A A B.Graphical Evaluation and Review Technique［M］.Santa Monica:Rand Corp，1966．

［6］Reza A，Hamid R G，Shamsollah A，et al.Modeling and Analysis of Mechanization Projects of Wheat Production by GERT Networks［J］.Agricultural Sciences in China，2010，9（7）:1078-1083．

［7］谢家平，赵忠.基于GERT随机网络的废弃回收预测模型研究［J］.管理学报，2010，7（2）:294-300．

［8］方志耕，杨保华，陆志鹏，等.基于Bayes推理的灾害演化GERT网络模型研究［J］.中国管理科学，2009，17（2）: 102-107．

Prediction for Ordering Interval of Armament’s Maintenance Spare Parts Based on GERT

SHAO Yan-jun1，MA Chun-mao2，PAN Hong-xia1，LIU Yong-jiang1
（1.Mechanical and Power Engineering College，North University of China，Taiyuan 030051，China；2.North west Institute of Mechanics and Electrics Engineering，Xianyang 712099，China）

As the weapon equipment repair spare parts demand is random，so it is difficult to accurately predict the order interval.For such a demand systems of random fluctuations，this paper proposes the use of GERT random network model to describe it，and then derives the analytic expression of random order interval in demand，solves the prediction problem of uncertain demand’s order interval.It provides data support for the scientific management of weapon equipment repair parts.Experiments show that，GERT random network model is an effective method to make sure the ordering interval of armament’s maintenance spares.

GERT model，stochastic volatility，ordering interval，maintenance spare parts

TJ307

A

1002-0640（2015）04-0038-03

2014-03-02

2014-04-07

国家自然科学基金（51175480）；山西省自然科学基金资助项目（2012011046-12）

邵延君（1972- ），男，内蒙古赤峰人，博士。研究方向：武器装备的维护与管理、装备故障诊断等。