左右兼顾——谈分段函数问题的解答

☉江苏省平潮高级中学 周 炎

左右兼顾
——谈分段函数问题的解答

☉江苏省平潮高级中学 周 炎

分段函数是高考的热点之一，分段函数，顾名思义，其函数在不同定义域范围内，有不同的解析式，其内容涉及求值、定义域、值域、解析式、奇偶性、单调性、图像、方程、不等式等多方面知识.因此在处理分段函数问题时必须左右兼顾，方可防止错解.下面举例说明.

一、针对不同自变量，由内到外逐层求函数值

解析：当a≥1时，f（a）=2a>1，所以f（f（a））=2f（a）；当a<1时，f（a）=3a-1.若f（f（a））=2f（a），则f（a）≥1，即3a-1≥1，所.故选C.

点评：不同的自变量，有不同的解析式，针对不同自变量，选取对应函数表达式，由内到外逐层求函数值.

二、“不重不漏”求分段区间的解析式

例2（2014年安徽高考）定义在R上的函数f（x）满足f（x+1）=2f（x），若当0≤x≤1时，f（x）=x（1-x）.则当-1≤x≤0时，f（x）=___________.

解析：当-1≤x≤0时，有0≤x+1≤1，则f（x+1）=（x+ 1）［1-（x+1）］.

又因为f（x+1）=2f（x），所以2f（x）=（x+1）［1-（x+1）］.

点评：“求谁设谁”，求哪个区间的解析式，x就设在哪个区间内，然后代入已知区间的解析式，利用奇偶性解出f（x）.求分段函数的解析式时，分别求出定义域内各段对应的解析式，再组合在一起，要注意各区间内的点要“不重不漏”，求哪个区间的解析式，就把x设在哪个区间上.

变式：已知y＝f（x）+x2是奇函数，且f（1）＝1.若g（x）＝f（x）+2，则g（-1）＝________.

答案：-1.

三、分段函数的单调性，由局部到整体

例3（2015年北京高考模拟）已知a>0，函数f（x）=则实数t的取值范围为（）.

点评：本题属于利用函数单调性求参数范围问题，判断分段函数的单调性时，首先应该判断各段函数的单调性，若每一段函数单调性一致，再判断分界点处函数值的关系，符合单调性定义，则该函数在整个定义域上单调递增或递减，不符合，则必须分段说明单调性.

四、分段函数的奇偶性的分段处理

A.f（x）是偶函数B.f（x）是增函数

C.f（x）是周期函数D.f（x）的值域为［-1，+∞）

解析：由函数f（x）的解析式知，f（1）＝2，f（-1）＝cos（-1）＝cos1，f（1）≠f（-1），则f（x）不是偶函数.当x>0时，令f（x）＝x2+1，则f（x）在区间（0，+∞）上是增函数，且函数值f（x）>1；当x≤0时，f（x）＝cosx，则f（x）在区间（-∞，0］上不是单调函数，且函数值f（x）∈［-1，1］；所以函数f（x）不是单调函数，也不是周期函数，其值域为［-1，+∞）.故选D.

点评：分段函数奇偶性的判断方法：先看定义域是否关于原点对称，若不对称就为非奇非偶函数；若对称，且分别从相对称的两个区间上满足相同关系时，才具有确定的奇偶性.

五、多变量下的分段函数，由多化一

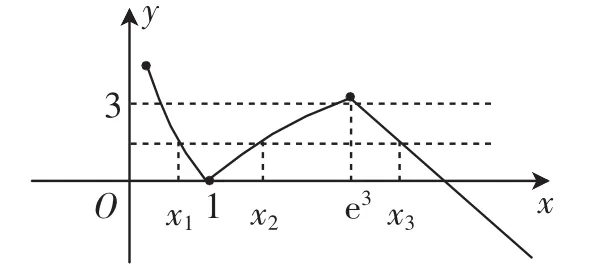
图1

解析：作出分段函数f（x）的图像，如图1所示，由图可知，只有当直线位于y=0与y=3之间时才与函数f（x）的图像有3个交点，结合图像可得1

点评：多变量下的分段函数要结合函数的图像特征求出变量的范围，同时要结合函数的表达式求出各变量之间的关系，将多变量问题转化为单变量的函数问题，再结合定义域准确求出最值或范围.

变式：设f（x）是定义在R上且周期为2的函数，在区间［-1，1］上，f（x）其中a，b∈R.若则a+3b的值为________.

答案：-10.

六、分段函数零点问题转化为交点问题处理

解析：分析题意可知，问题等价于方程x3=b（x≤a）与方程x2=b（x>a）的根的个数和为2.若两个方程各有一个根，则可知关于b的不等式组有解，从而a>1；若方程x3=b（x≤a）无解，方程x2=b（x>a）有2个根，则可知关于b的不等式组有解，从而a<0.

综上，实数a的取值范围是（-∞，0）∪（1，+∞）.

点评：函数的零点个数问题，通常转化为函数图像交点个数问题处理.本题中的零点问题可转化为y=f（x）与y=b有两个交点问题，y1=x3为单调函数，故其与y=b至多有一个交点；而y2=x2与y=b有1个或2个交点，题目中g（x）=f（x）-b有两个零点，问题等价于y1，y2与y=b各有一个交点，或y1与y=b没有交点，y2与y=b有两个交点.

①若a=1，则f（x）的最小值为________；

②若f（x）恰有2个零点，则实数a的取值范围是______.

综上，分段函数函数问题的常用处理方式，即分别处理不同定义域内的不同解析式，从而函数值域、最值、单调性、奇偶性、零点等问题就会迎刃而解，另外方程、不等式等可用数形结合思想、等价转化思想、分类讨论思想及函数思想来解，可使问题得到大大简化.