接天莲叶无穷碧，映日荷花别样红——对2015年一道高考题的拓展研究

☉江苏省石庄高级中学 肖雄伟

接天莲叶无穷碧，映日荷花别样红
——对2015年一道高考题的拓展研究

☉江苏省石庄高级中学 肖雄伟

高考试题是命题组集体智慧的结晶，一道具有典型性、代表性的试题不仅能考查学生的数学素养，还能起到高校选拔的功能，还应具有进一步探索、研究的价值.笔者对2015年高考数学新课标1卷理科第20题进行了思考探究并做引申推广，欢迎指正.

一、题目再现

（2015年高考数学新课标1卷理科第20题）在直角坐标系xOy中，曲线C：与直线y=kx+a（a＞0）交与M、N两点.

（Ⅰ）当k=0时，分别求C在点M和N处的切线方程；

（Ⅱ）y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？说明理由.

本题综合考查了直线与抛物线的位置关系，涉及的知识点有求切线方程，动直线中的定量关系等，体现了数形结合、方程等数学思想.试题难度适中，立意深刻，题面新颖，能较全面地检查学生平面解析几何的学习水平.

（Ⅱ）存在符合题意的点P（0，-a）.（过程略）

二、拓展研究

解完此题，笔者不禁思考，直线恒过点（0，a），与点P关于原点对称，可否将题中的条件和结论一般化呢？答案是肯定的，于是得到以下结论.

结论1：已知抛物线C：x2=2py（p>0），如果过定点（0，t）（t>0）且不与y轴垂直的直线l与抛物线C交于M、N两点，则在y轴上存在点P（0，-t），使得∠OPM=∠OPN.

证明：设直线l的方程为y=kx+t（k≠0），M（x1，y1），N（x2，y2），直线PM、PN的斜率分别为k1、k2.将y=kx+t代入C并整理得x2-2pkx-2pt=0，则x1+x2=2pk，x1x2=-2pt.即∠OPM=∠OPN.结论成立.

对于焦点在x轴上的抛物线，结论也是成立的.

结论2：已知抛物线C：y2=2px（p>0），过定点（t，0）（t> 0）且不垂直于x轴的直线l与抛物线C交于M、N两点，则在x轴上存在点P（-t，0），使得∠OPM=∠OPN.

证明方法同上，此处略.

我们知道，椭圆、双曲线、抛物线都属于圆锥曲线，上述结论类比到椭圆与双曲线上也成立吗？答案是肯定的，于是就有了如下的结论.

证明：设直线l：x=my+t（m≠0），M（x1，y1），N（x2，y2），由直线l与椭圆C的方程联立得：（a2+b2m2）y2+2b2mty+

因此∠OPM=∠OPN.

证明可仿照前面几个结论的方法证得，此处不再赘述.

波利亚说，好问题就像蘑菇，它们是成群出现的，在解决一个问题以后，自然就会思考此问题相应的逆命题是否成立，通过探究可以发现如下结论.

三、逆向思考、变式探究

结论5：已知抛物线C：y2=2px（p>0），点P（-t，0）（t> 0），设不垂直于x轴的直线l与抛物线C交于M、N两点，若∠OPM=∠OPN，则直线l过定点（t，0）.

证明：设直线l：x=my+n（m≠0），M（x1，y1），N（x2，y2），由直线l与抛物线C的方程得y2-2pmy-2pn=0，则y1+y2= 2pm，y1y2=-2pn.

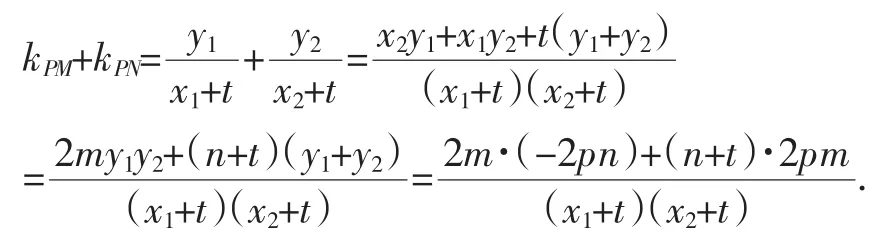
由∠OPM=∠OPN，得kPM+kPN=0，即2m·（-2pn）+（n+ t）·2pm=0，解得n=t，从而直线l的方程为x=my+t，故直线l过定点（t，0）.

证明：设直线l：x=my+n（m≠0），M（x1，y1），N（x2，y2），联立直线l与椭圆C的方程得（a2+b2m2）y2+2b2mny+b2（n2-

因为∠OPM=∠OPN，所以kPM+kPN=0，即2m·解得n=t，从而直线l的方程为x=my+t，故直线l过定点（t，0）.

结论的证明可仿照结论5、6的证明方法证得，此处不再赘述.

四、高考链接

此类问题的出现不是第一次，在前几年的高考中也出现过，今年的四川卷理科第20题也考到类似的背景.

（1）求椭圆E的方程.

（2）在平面直角坐标系xOy中，是否存在与点P不同的定点Q，使得恒成立？若存在，求出点Q的坐标；若不存在，请说明理由.

五、结束语

高考题是考生复习备考的至尊法宝，认真研究高考题，发掘其真正的内涵，探索出新的规律性结论，并运用于教学之中，可以丰富我们的教学，使我们的教学理念更新，解题的手段升级.因此，高中一线教师必须养成经常研究高考试题的好习惯，真正领会高考试题命制的背景、意图及其蕴含着的真谛，只有通过解题过程的分析、延伸、拓广，才能让数学教学充满生机和活力，使学生充分享受数学学习的乐趣，乐教乐学，才是数学教学的最高境界！