基于类比思想的物理教学实践探讨
郭健

【摘 要】类比是科学研究中的一种重要的思想方法,物理教学注重学生的技能训练、能力培养。本文对高中物理的新课教学及习题教学中渗透类比思想的教学实例初步的作了探讨和总结。
【关键词】类比;思想方法;物理教学;实践探讨
类比法是根据两类对象之间在某些方面的类似或相同, 而推断它们在其它方面也可能类似或相同的逻辑思维方法。类比法是科学发展中非常重要的一种研究方法,也是探索新知和改进创新的重要途径之一。如果我们在新形势的课堂教学实践中适当地渗透并应用类比法,可以让学生更好地理解相关的理论知识,并提高他们的科学素养、创新能力和探索精神。
1.类比法在新授课中对旧有知识的引导与衔接
物理学各部分规律及概念之间均有存在的内在联系。在课堂上,通过对新旧知识进行类比,使学生易于理解相对抽象的新知识,同时也巩固了旧知识,还帮助学生建立统一的知识体系。以下几例均能以类比引入新课,化抽象为形象,最终提高课堂的学习效率。
实例1:静电场与引力场的类比。进行静电场一章的教学时,可以将它与引力场进行类比,可以帮助学生较容易的理解相对抽象的电场。
1.1两种场力的表达形式类比。
引力场:F=G;电场:F=k。都满足平方反比规律。
1.2两种场的强弱概念类比。
为了较容易的理解E的定义,可以首先复习万有引力与地球上物体所受重力关系F=mg,然后可以提问:同样的物体,在月球表面要比在地球表面重力小的多,说明两星球表面的什么物理量不同?它与物体的质量有关吗?可能与什么因素有关?这样通过类比,可以较快速的得出,在电场中,任意点的电场强度E由场源电荷决定而与试探电荷电量无关,从而推导出E=。
1.3两种场的能量表达类比。
电势能与重力势能关系相似:重力场中,重力做功引起重力势能变化;而电场中,电场力做功引起电势能变化。变化关系及物理量使用上也相似:电势类比高度,两者都具有相对性;电势差类比高度差;等势面类比等高线。各量可以在公式W=qU与W=mgh的对比中一一类比。
类似地,在磁场部分的教学时,同样可以对电场与磁场性质进行类比。在电场中,任意点的电场强度E由场源电荷决定而与试探电荷无关,可类比为:在磁场中,任意点的磁感应强度也由场源决定,与放置的电流元无关。从而引出B的定义式B=。另外对于此定义式的理解,同样可类比E=、U=这几个公式,指出式中定义出的量都与等号右侧各量是无关的。这有助于我们较容易和深刻的理解“场”这一抽象的概念。
例2: 玻尔模型的能级与跃迁理论也是很抽象的知识点,可类比卫星绕地球的运行。例如可以提问:当卫星要运行得离地球更远一些时,需要加速还是减速;到达更远轨道时,卫星的速度是否比较原来变快了?这几个问题学生是较易理解的,玻尔能级理论与跃迁时吸收或辐射能量的探讨也就很容易的进行了。
例3:分子间的作用力与势能,可以类比为水平方向上的弹簧所连接小球受到的弹力与弹性势能。
如上图1所示,三种情况分别可类比两分子之间的距离rr0三种情况,势能的情况也同样可以类比。这样学生就较易理解分子力这一较抽象的概念。
2.类比法在解决习题过程中对陌生模型的迁移与转化
在物理教学中,很多新的知识与旧知识在思想、方法等方面都有着一定的联系,此基础上通过类比可以探索出很多新知识、新方法。高考试题在平时的练习中,学生往往不可能碰到,是一些相对全新的情景或模型,但是考纲又明确告知不可能脱离高中物理的教学实际,这二者并不矛盾。这就体现在碰到陌生的问题时,要求学生运用包括观察、归纳、类比、猜想、联想、直觉、灵感等各种思维过程的综合运用,作出一个从条件到结论的合情推理,最终寻得解题思路。类比,正是其中必不可少的重要途径之一。在平时的习题教学中贯彻类比思想,可以极大地激发出学生的兴趣,符合了学生的好奇与探究的心理,最终提高学生解题与创新能力,并能在最终的考试中胜出。例如:
2012北京高考物理23题:摩天大楼中一部客运电梯,行程超过百米,简化模型如下图2,电梯的加速度a随t是变化的。已知在t=0时由静止开始上升,a-t图像如图2所示。电梯总质量m=2×103kg,忽略一切阻力,g=10m/s2。
(1) 求电梯在上升过程中受到的最大拉力F1和F2最小拉力;
(2)类比是一种常用的研究方法,对于直线运动,教科书中讲解了由v-t图像求位移的方法。请你借鉴此方法对比加速度和速度的定义,根据图3所示a-t图像,求电梯在第1s内的速度改变量△v1和第2s末的速度v2;
(3)求电梯以最大速度上升时,拉力做功的功率P,再求0-11s时间内,拉力和重力对电梯所做的总功W。
题目本身是一个包括变加速运动在内的多过程问题,难度中等。关键我们来观察一下第2小问题,题设中要求对a-t图像分析后,求速度的变化量,如果没有关于“类比是……”这一段的提示,学生可能没办法下笔。因为对于变加速运动过程,需要用到高等数学的思想。但是由v-t图像来求位移大小,学生都熟悉。通过题中提示:结合a与v的定义,通过自己的类比思考,就能想到a-t图像与坐标轴所围面积即为△v。即可求得第1s内的速度改变量△v1=0.5m/s,前2秒内△v2=v2-v0=1.5m/s,第2s末的速度v2=1.5m/s。
高考考题越来越倾向于体现考能力,考素质,考题中涌现新模型时,学生的心理素质和平时的方法训练就显得尤为重要,类比法能让学生联想和借鉴平时所熟知的模型,通过比较并借用相类似的方法就能快速的找到解题的突破口了。我们再来看下面一例:
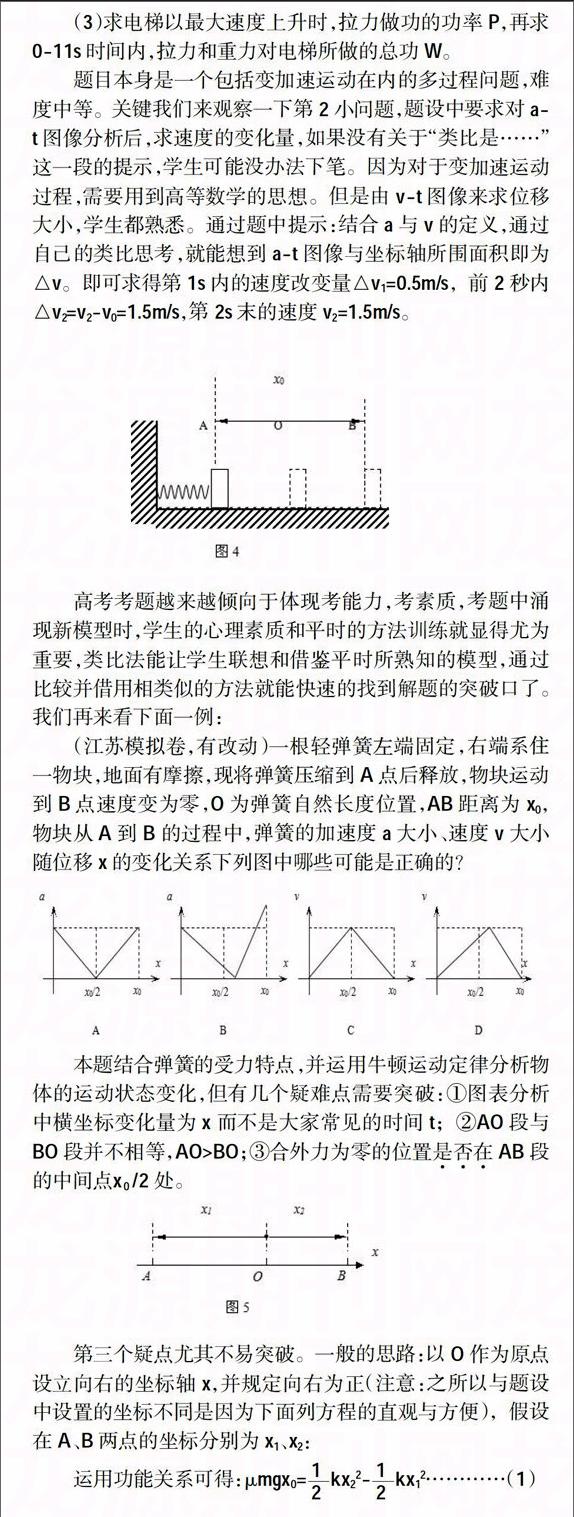
(江苏模拟卷,有改动)一根轻弹簧左端固定,右端系住一物块,地面有摩擦,现将弹簧压缩到A点后释放,物块运动到B点速度变为零,O为弹簧自然长度位置,AB距离为x0,物块从A到B的过程中,弹簧的加速度a大小、速度v大小随位移x的变化关系下列图中哪些可能是正确的?
本题结合弹簧的受力特点,并运用牛顿运动定律分析物体的运动状态变化,但有几个疑难点需要突破:①图表分析中横坐标变化量为x而不是大家常见的时间t;②AO段与BO段并不相等,AO>BO;③合外力为零的位置是否在AB段的中间点x0/2处。
第三个疑点尤其不易突破。一般的思路:以O作为原点设立向右的坐标轴x,并规定向右为正(注意:之所以与题设中设置的坐标不同是因为下面列方程的直观与方便),假设在A、B两点的坐标分别为x1、x2:
运用功能关系可得:μmgx0=kx22-kx12…………(1)
再由上图可知关系式:x0=x2-x1………………………(2)
联立(1)(2)两式,解得μmg=k,这个结果说明:平衡位置是在AB段的中点。
但是,且不说弹簧的势能方程学生是否能运用,仅从功能关系来讨论位移与形变量的思路很多学生就想不到。那是否有其他简捷的思路可以解决这一问题呢?事实上如果学生对弹簧振子熟悉,并能够举一反三,就可作如下类比:
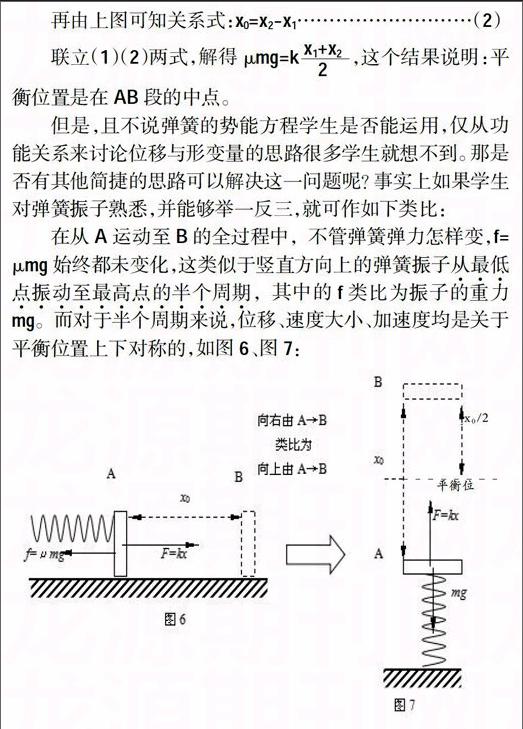
在从A运动至B的全过程中,不管弹簧弹力怎样变,f=μmg始终都未变化,这类似于竖直方向上的弹簧振子从最低点振动至最高点的半个周期,其中的f类比为振子的重力mg。而对于半个周期来说,位移、速度大小、加速度均是关于平衡位置上下对称的,如图6、图7:
学过振动后,弹簧振子是很易理解和记忆的模型。这样疑难点就迎刃而解了:平衡位置确实不在O点而是在AB的中点x0/2处。就可以很容易的找到正确答案AC了。
新题目、新模型都不怕,怕的就是我们在平时的教学中只对学生作知识的灌输而不对学生因势利导的进行各类思想方法的训练、科学素养的培养。我们每一道物理习题的解题思路的产生,都有赖于教师在教学中将这种“授人以渔”的思想渗透到平时教学的点滴中。每一节新课的引导、每一道解题思想的启发、甚至于每一次课后师生之间的教与学的交流谈话。
3.总结
类比是重要的科学研究的思想方法,是合情推理的重要组成部分,在物理中可以帮助我们揭示物理规律之间的内在联系、启发我们独特的解题思路,只有平时上课及解题过程中引导学生真正经历阅读、动手、思考、研讨等过个过程,多尝试领悟,才能对物理这一门学科学通学透。
当然,类比作为一种逻辑思维方法,既不同于归纳方法,也不同于推理方法;由类比法推出的假设并不一定是正确的,这些结论必须要经过实验证明才能进一步推广。因此,要注意应用类比法教学的正确性和适当性,不能一概而论。
【参考文献】
[1]王小兰.巧用类比法实现物理课堂有效教学途径探讨. 《电子世界》.2013.5
[2]申建中.引力场与静电场的类比.《数理化研究》.2008.3
(作者单位:陆慕高级中学)

