浅谈利用变式进行运动型问题的复习

高云芳

摘 要 运动型问题常常与探究性问题、分类讨论问题结合在一起，学生在解答此类问题时普遍感到困难，若设计变式题组进行运动型问题复习，由易到难、循序渐进，有利于提高学生对运动型问题的分析、解决能力。

关键词 探究 运动型 问题 变式 能力

中图分类号：G633.6 文献标识码：A 文章编号：1002-7661（2015）11-0041-03

一、利用习题变式，培养学生探究运动型问题的意识

在运动型复习的教学中，把问题由静态情景变为动态情景，由特殊位置到一般情形，变解题模式为“探究式”。 变式题可满足学生的好奇心，培养学生学习数学的兴趣，使学生掌握运动型问题中“动静互化”，有利于培养学生探究、解决运动型问题的意识。

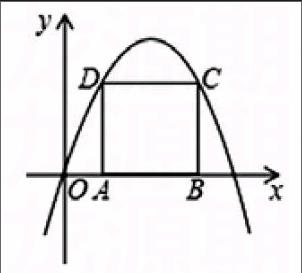
例：如图，一条抛物线y=ax2+bx（a≠0）的顶点坐标为（2，），正方形ABCD的边AB落在x轴的正半轴上，顶点C、D在这条抛物线上。

（1）求这条抛物线的表达式；

（2）求正方形ABCD的边长。

分析：（1）设抛物线顶点式解析式y= a（x-2）2+，

然后把原点坐标代入计算求出a的值即可得解；故抛物线解析式为y= - x2+ x；

（2）设正方形的边长为2m，根据抛物线的对称性求出点C的坐标，然后代入抛物线解析式计算解得m1=1，m2= -4（舍去），所以正方形ABCD的边长为2m=2？=2。

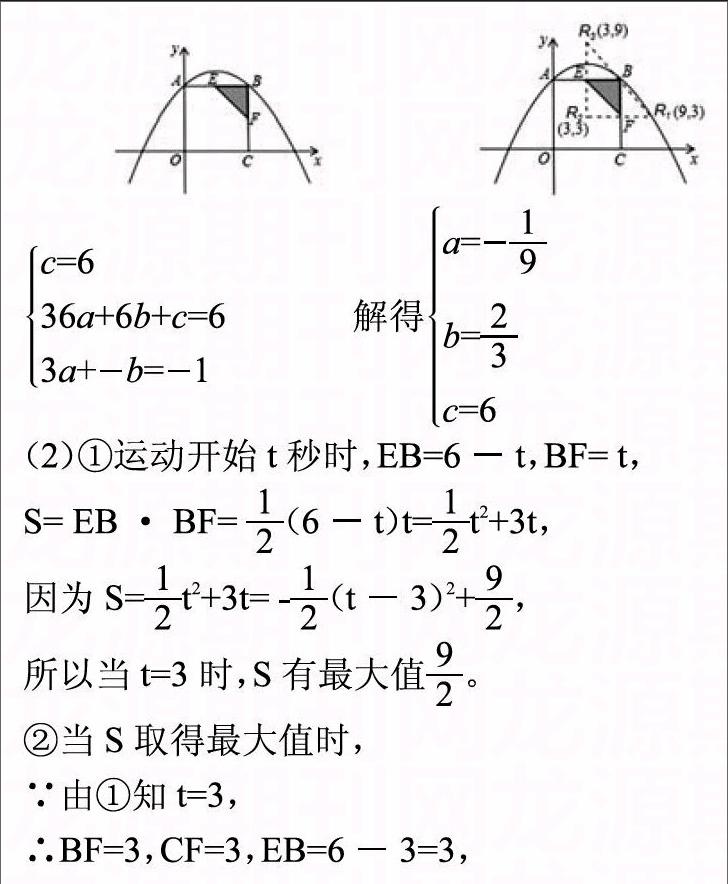
变式一 ：如图，在直角坐标系xOy中，正方形OCBA的顶点A，C分别在y轴，x轴上，点B坐标为（6，6），抛物线y=ax2+bx+c经过点A，B两点，且3a-b=-1。

（1）求a，b，c的值；

（2）如果动点E，F同时分别从点A，点B出发，分别沿A→B，B→C运动，速度都是每秒1个单位长度，当点E到达终点B时，点E，F随之停止运动，设运动时间为t秒，△EBF的面积为S。

①试求出S与t之间的函数关系式，并求出S的最大值；

②当S取得最大值时，在抛物线上是否存在点R，使得以E，B，R，F为顶点的四边形是平行四边形？如果存在，求出点R的坐标；如果不存在，请说明理由。

若存在某点R，使得以E，B，R，F为顶点的四边形是平行四边形，则FR1=EB且FR1∥EB，即可得R1为（9，3），R2（3，3）；或者ER3=BF，ER3∥BF，可得R3（3，9）。

再将所求得的三个点代入y=x2+ x+6，可知只有点（9，3）在抛物线上，因此抛物线上存在点R（9，3），使得四边形EBRF为平行四边形。

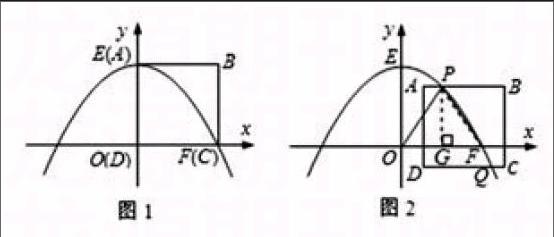
变式二 ：如图1，在平面直角坐标系中，抛物线y=ax2+c与x轴正半轴交于点F（16，0），与y轴正半轴交于点E（0，16），边长为16的正方形ABCD的顶点D与原点O重合，顶点A与点E重合，顶点C与点F重合。

（1）求抛物线的函数表达式；

（2）如图2，若正方形ABCD在平面内运动，并且边BC所在的直线始终与x轴垂直，抛物线始终与边AB交于点P且同时与边CD交于点Q（运动时，点P不与A，B两点重合，点Q不与C，D两点重合）。设点A的坐标为（m，n）（m>0）。

利用变式，设计由易到难的问题，引导学生通过适当模拟，分类画图，找出分类的关键点，从而得出取值范围。

二、利用习题变式，提高学生探究运动型问题的能力

利用习题变式，在学生解题过程中，引导学生从不同角度去思考和探索问题，并从中获得对问题的深刻理解，不断提高解决运动型问题的能力。

变式三 ： 如图①，边长为4cm的正方形ABCD的顶点A与坐标原点0重合，边AB在x轴上，点C在第四象限，当正方形ABCD沿x轴以1cm/秒的速度向右匀速运动，运动时间为t秒时，经过A、B两点的抛物线y=ax2+bx+c与y轴相交于E点，其顶点为M。

（1）若正方形ABCD在运动过程中，抛物线y=ax2+bx+c的顶点M保持在正方形的内部，求a的取值范围。

（2）设正方形ABCD在运动过程中，△ABE与△ABM的面积比为k，求k与运动时间为t（秒）之间的关系式。

（3）当正方形ABCD沿x轴向右运动2秒钟时，在抛物线y=ax2+bx+c上存在一个点P，使△ABP为直角三角形，且△OPA∽△OBP，求此时抛物线的解析式。

（1）求此抛物线的表达式；

（2）正方形ABCD沿射线CB以每秒个单位长度平移，1秒后停止，此时B点运动到B1点，试判断B1点是否在抛物线上，并说明理由；

（3）正方形ABCD沿射线BC平移，得到正方形A2B2C2D2，A2点在x轴正半轴上，求正方形ABCD的平移距离。

利用变式设计运动型的问题，引导学生适当模拟，画出特殊图形，实现“化动为静”，最后将图形量化，建立方程模型。