Rikitake双盘发电机系统的状态反馈控制
雷腾飞 ,尹劲松 ,陈 恒 ,任林政
(1.西京学院 控制工程学院,陕西 西安 710123;2.山东泰开自动化有限公司,山东 泰安 271000)
1 引言
1963年,美国科学家lorenz在天气预报的模型中发现了“蝴蝶效应”,从此许多科研工作者走进了有关混沌领域的研究[1].随着人们对混沌的深入研究探索,混沌理论在图像数据加密[2]、信号检测与处理[3]、机电控制系统[4]等领域得到了广泛应用.
地磁场长期变化中的极性反转是地磁理论中需要且最难说明的问题之一.对此地磁学家们提出了反转电机、统计、圆盘发电机等模型描述,其中双盘发电机模型为地磁学家们解释地磁起源提供了理论依据.该模型在1958年被地磁学家Rikitake提出[5],文[5]验证了该模型含有丰富的混沌现象;文[6]对该系统采用比例微分方法对双盘发电机进行了控制,文[7]采用了自适应方法对系统进行了控制,但由于每个状态量都含有控制器,则很难在工程与实际系统中实现.张济仕等研究了此模型的分数阶模型并进行了控制[8],但在工程中分数阶模型用的较少.自从Ott、Grbogi及Yorker提出混沌控制方法与理论以来,运用于永磁同步电机的控制方法已有很多文献研究[9-11],雷腾飞等对非均匀气隙的电机进行了分析与控制[12],但对于双盘发电机混沌系统有效的控制方法报道却不多.因此在众多的控制方法中采用一种有效的控制方法,使系统避免混沌产生显得极其重要且具有现实意义.
本文针对双盘发电机混沌系统,利用相位图、分岔图,Lyapunov指数等分析了双盘耦合发电机系统的动力学行为,研究了耦合发电机系统对参数的敏感性;在考虑控制方法能够有效的应用到工程及实际背景下,采用线性状态反馈控制方法对Rikitak发电机混沌行为进行了控制,使得系统快速准确的达到了控制的目标.
2 双盘发电机的数学模型与混沌特性
20世纪50年代,日本地磁学家Rikitake年提出了发电机的模型,双盘发电机由两个圆盘与两个相互耦合在一起的线圈组成.经过时间尺度变化与映射得到模型的无量纲方程如下[6]
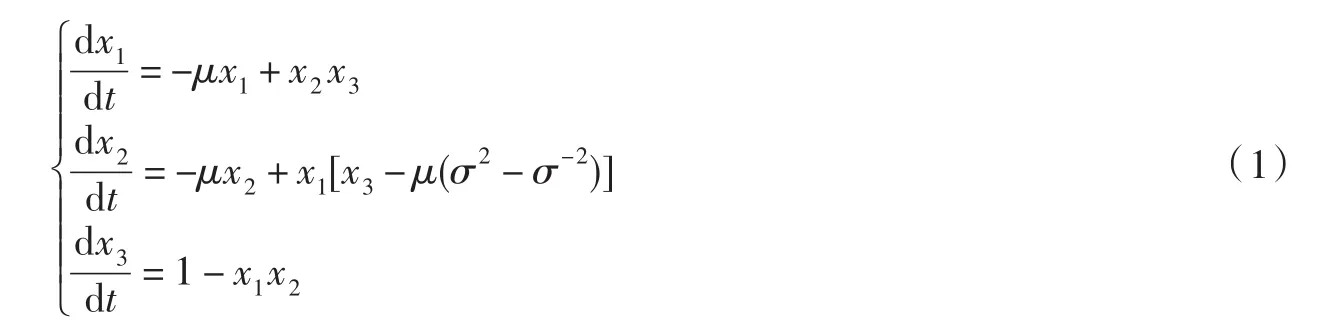
其中x1,x2表示无量纲的发电机电流,x3表示两两个圆盘的角速度,μ和σ表示正的控制参数.
2.1 耗散性
双盘耦合发电机系统的耗散性可由(1)导出:

这就意味着系统(1)具有耗散性,且以指数速率e-2t收敛,当t→∝时,包含系统轨线的每个体积元以指数速率收缩到零.则双盘耦合发电机系统渐近固定在一个吸引子上,即说明混沌吸收引子存在性.
2.2 双盘耦合发电机系统平衡点的分析
设系统(1)的平衡点为 E0=(x10,x20,x30),可以得到:x10=±σ,x20=±σ-1,x30=μσ2.
为了分析平衡点的稳定性,得到平衡点E0的Jacobian矩阵:

将平衡点E0=(x10,x20,x30)代入式(3),求出在此平衡点处的Jacobian矩阵的特征方程:


图1 系统的相位图
2.3 参数 μ对系统的影响
双盘发电机正参数 μ受工作环境,噪声等因素影响比较大,随着参数 μ的变化,可以看出系统出现了极为丰富的混沌现象,当 μ∈[0.5,2.5]时,系统处于混沌状态;当μ∈[1,0.5]⋃[2.5,4]时,系统处于周期状态.如图2所示.
当系统处于混沌运动时,发电机发出的电流与电压忽高忽低,电流与电压的这种突变很容易引起系统的崩溃,因此须找出一种合适有效的方法消除或抑制系统中的混沌行为.
3 状态反馈控制器的设计
3.1 非线性系统控制理论
考虑如下不受控的非线性自治系统

其中X为系统状态变量,α为系统参数;在平衡点附近E0处对系统线性化,则系统(5)近似为:


其中可取B为对角矩阵,u为控制器,且

式中,K为反馈增益矩阵.
本文利用控制论中极点配置的方法来确定反馈增益矩阵K,从而使系统迅速达到稳定状态.
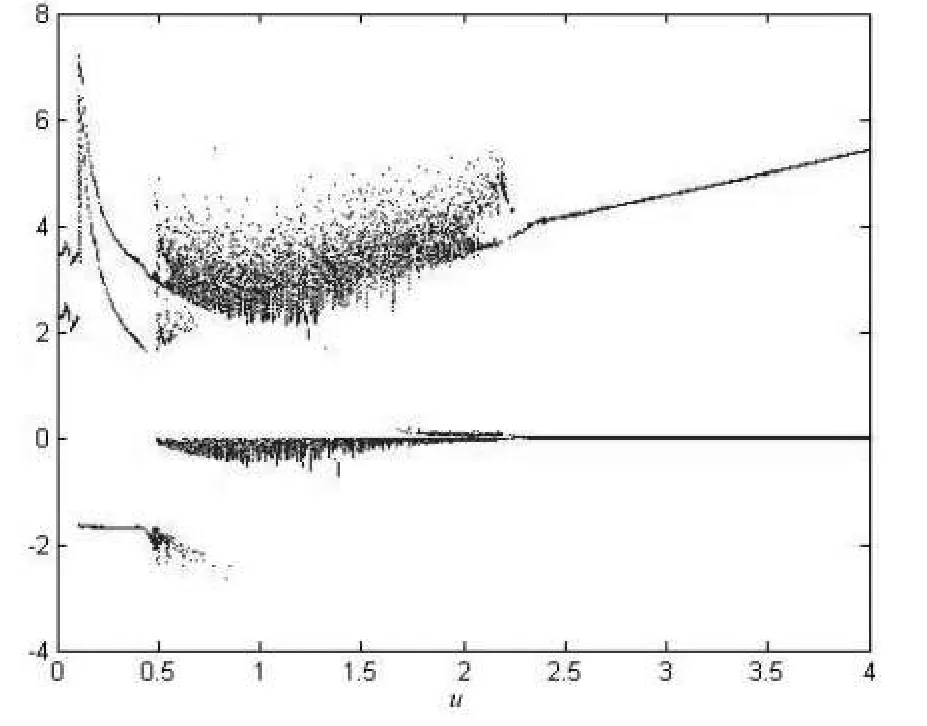
图2 系统的分岔图
3.2 控制器设计
根据上述理论,考虑系统(1)加入反馈控制器,u=K(X-E0),则系统(1)的受控系统为:
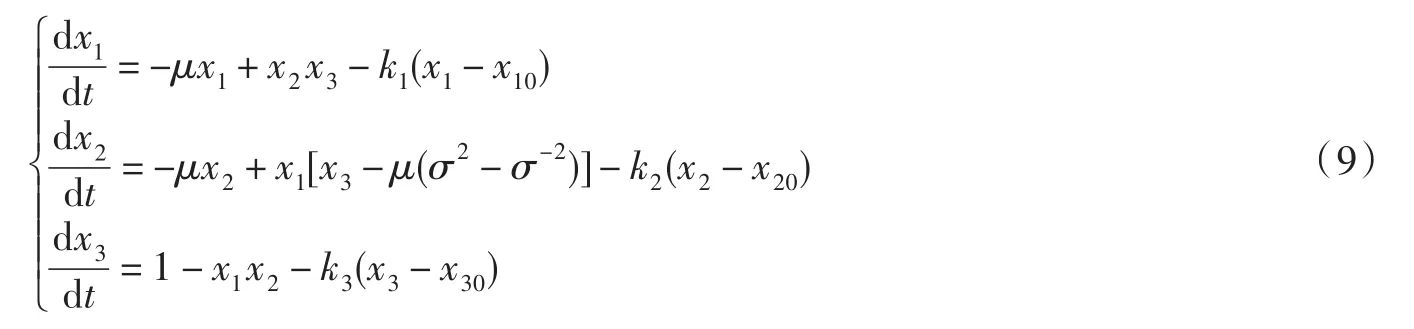
根据(7)可以简化B,取 B=diag(1,1,1).
则系统(9)在系统(1)平衡点E0下的Jacbian矩阵为:

则受控系统的特征方程:

其中,A1、A2,、A0都是与 k1、k2、k3有关的系数.
取希望配置的极点(-1,-1,-10),则极点构成的特征多项式为:

极点的特征多项式(12)与受控系统的特征多项式(11)相同,求出k1=9,k2=0,k3=1.当系统运行到20 s时,加入状态反馈控制器,运用Matlab仿真,仿真系统结果见图3.从图3可以发现,在接入控制器后,系统迅速达到稳定状态,且响应速度快鲁棒性好.
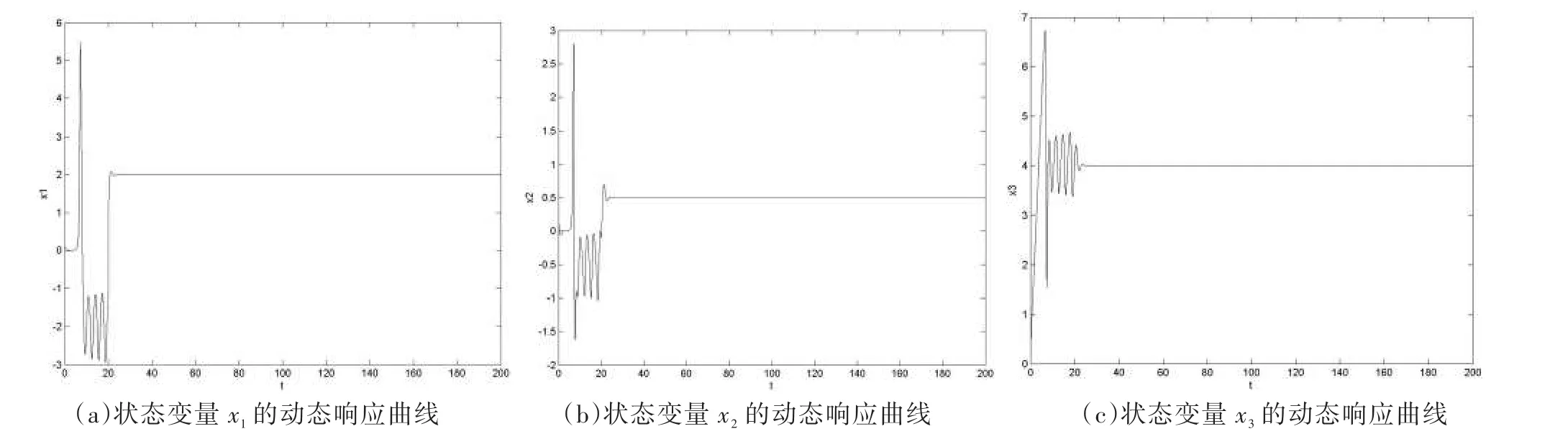
图3 受控系统的运动状态
4 结论
本文研究了Rikitake双盘发电机模型,研究表明模型具有混沌运动,此外,还进行了Rikitake双盘发电机模型混沌机理研究.针对该发电机非线性特性,设计状态反馈控制器并应用于本系统.仿真结果表明系统在控制器的作用下能够迅速达到稳定状态,理论分析与数值仿真结果相一致.仿真结果进一步验证了所用控制方法的有效性,对机电与电机系统控制提供了理论参考价值.
[1]Lorenz E N.Deterministic nonperiodic flow[J].J Atmos Science,1963,20(2):130-141.
[2]Ren H P,Baptist M,Grebogi C,Wireless communication with chaos[J].Physics Review Letter,2013,110(18):184101.
[3]任海鹏,刘丁.基于贝努力映射和CPLD的混沌A/D转换器[J].仪器与仪表学报,2007,28(1):42-47.
[4]雷腾飞,陈恒,王震,等.分数阶永磁同步风力发电机中混沌运动的自适应同步控制[J].曲阜师范大学学报(自然科学版),2014,40(3):63-68.
[5]I Keisuke.Chaos in the Rikitake two disk dynamo system[J].Earth and Planetary Science Letters,1980,51(2):451-456.
[6]雷腾飞,陈恒,王荣,等.变形Rikitake双盘耦合发电机系统的动力学分析与控制[J].济宁学院学报,2014,35(3):52-56.
[7]王春梅,常璐璐,申玉静.不确定变形祸合发电机系统的参数辨识与自适应同步[J].滨州学院学报,2008,40(3):85-90.
[8]张济仕,史蕊.分数阶Rikitake系统中的混沌及其控制[J].河南大学学报,2009,39(1):81-86.
[9]杨国良,李惠光.直驱式永磁同步风力发电机中混沌运动的滑模变结构控制[J].物理学报,2009,58(11):7552-7557.
[10]张兴华,丁守刚.非均匀气隙永磁同步电机的自适应混沌同步[J].控制理论与应用,2009,26(6):661-664.
[11]张波,李忠,毛宗源,等.一类永磁同步电机混沌模型与霍夫分叉[J].中国电机工程学报,2001,21(9):13-17.
[12]雷腾飞,陈恒,王荣.等,非均匀气隙永磁同步电机混沌系统的分析与控制[J].云南民族大学学报(自然科学版),2014,23(6):443-446.

