具有两个边界层的奇异摄动转向点问题的数值方法
耿发展
(常熟理工学院 数学与统计学院,江苏 常熟 215500)
奇异摄动问题在流体动力学、海洋大气层环流、化学反应、最优化控制等领域有着广泛的应用,因此,该问题引起了广大研究人员的兴趣.奇异摄动问题的解具有边界层的特性,经典的数值方法难以获得该类问题的精度较高的近似解.具有转向点的奇异摄动问题数值求解难度更大,寻求这类问题的有效数值方法更具挑战性.文献[1-4]讨论了这类问题的数值方法,本文基于再生核空间理论,提出求解具有两个边界层的奇异摄动转向点问题的有效数值方法.
1 数值方法
考虑下面的奇异摄动转向点问题:

其中函数a(x),b(x)和 f(x)是在-1<x<1内充分光滑.
依据a(x)的取值,方程(1.1)的解表现出边界层或内部层的特性.系数a(x)=0时点称为转向点.与非转向点问题相比,具有边界层或内部层的转向点问题处理起来往往更加棘手.这里,我们主要考虑如何解决具有边界层的奇异摄动转向点问题的情况.
假设:

在此假设下,问题(1.1)具有两个边界层.
1.1 问题(1.1)的转化
引入变量变换 x=h(s)=sin(π sin(π sin(πs/2)/2)/2),
问题(1.1)转化成了下面的新的边值问题
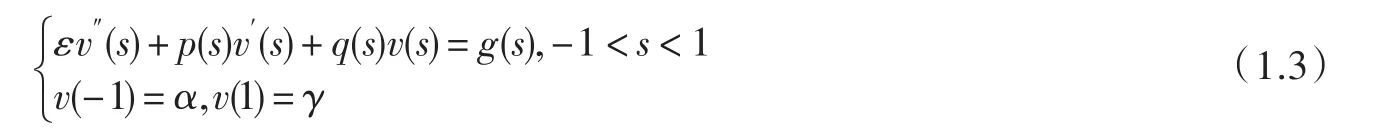
问题(1.3)的解不再具有边界层特性,处理起来比(1.1)容易得多,一旦得到(1.3)的解,(1.1)的解即可得到,下面我们将用再生核方法求解(1.3).
1.2 求解问题(1.3)的再生核方法
为了解决上述问题,引入一个未知函数

其中 ϕ(s)=γ0+γ1s,满足 ϕ(-1)=α,ϕ(1)=γ.
定义 Lv(s)= εv″(s)+p(s)v′(s)+q(s)v(s),问题(1.3)转化为

其中 F(s)=g(s)-Lϕ(s).
为了求解问题(1.5),我们构造下面的再生核空间W4[-1,1].
定义1.1 W4[-1,1]={u(x)|u‴(x)是绝对连续函数,且u(4)(x)∈L2[-1,1],u(-1)=0, }u(1)=0,W4[-1,1]的内积和范数分别表示为

和

定理1.1 W4[-1,1]为再生核空间,它的再生核表示为
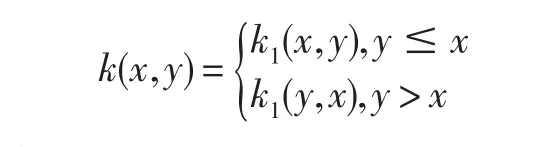
定理1.1的证明及再生核的求解方法参见文献[3,5].
不难证明,L:W4[-1,1]→W1[-1,1]为有界线性算子,从而其共轭算子 L*存在.记 φi(s)=kˉ(s,si)和ψi(s)=L*φi(s),对实施施密特正交化,即得
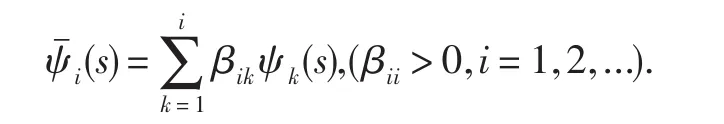
定理1.2 对于问题(1.5),如果在区间[-1,1]内是稠密的,那么为空间W4[-1,1]的完全系.
定理的证明过程见文献[6-7].
定理1.3 如果在区间[-1,1]内稠密,那么问题(1.5)的解可表示为

证明根据定理1.2,很显然有:是再生核空间W4[-1,1]的完全正交基.
进一步,我们可以得到
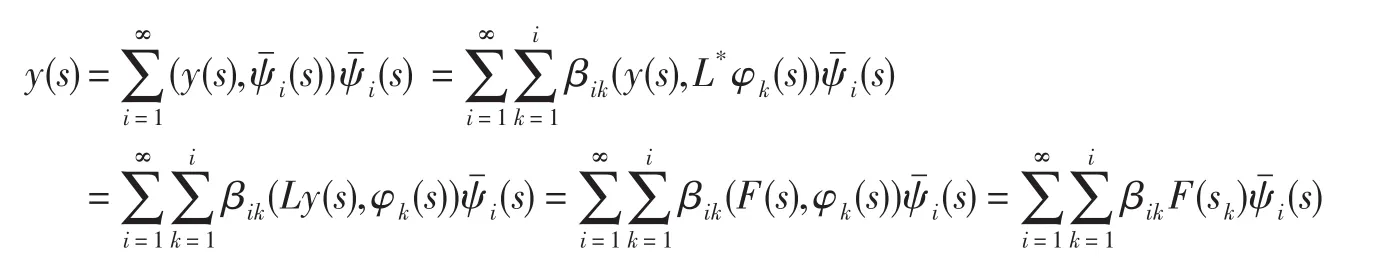
命题得证.
对级数表示(1.6)进行N项截断,便可得问题(1.5)的近似解.

定理1.4 问题(1.5)的近似解yN(x)及其导数y′N(s)一致收敛.
证明由于W4[lε,rε]是一个希尔伯特空间,显然有

由于

从而可得

命题得证.
由(1.4)及变量变换 x=h(s),可得(1.1)的近似解 uN(s)=vN(h-1(x)),其中 vN(s)=yN(s)+ϕ(s).
2 数值算例
考虑下面的奇异摄动问题

f(x)已知且保证问题的精确解是u(x)=e-2x(2x-1)/ε.使用本文提出的方法,取ε=2-8,2-12.本例所有的计算通过Mathemati⁃ca7.0完 成 ,所得的数值结果见图1,图2.
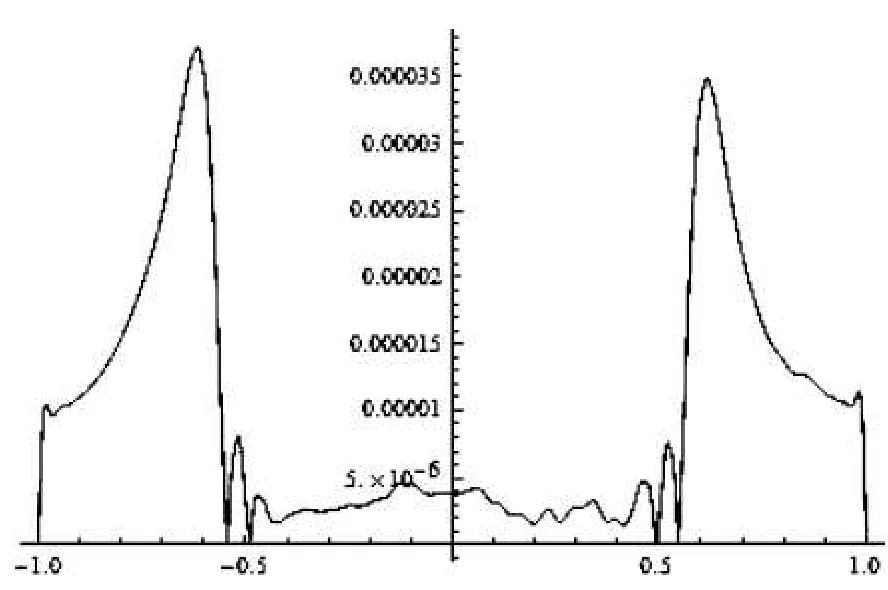
图1 ε=2-8时的绝对误差

图2 ε=2-12时的绝对误差
[1]Rai P,Sharma K K.Numerical method for singularly perturbed differential-difference equation with turning point[J].Int J Pure Ap⁃pl Math,2011,73(20):451-470.
[2]Kadalbajoo M K,Arora P,Gupta V.Collocation method using artificial viscosity for solving singularly perturbed turning point prob⁃lem having twin boundary layers[J].Comput Math Appl,2011,61:1595-1607.
[3]Geng F Z,Qian S P.Reproducing kernel method for singularly perturbed turning point problems having twin boundary layers[J].Ap⁃plied Mathematics Letters,2013,26:998-1004.
[4]Geng F Z,Qian S P,Li S.A numerical method for singularly perturbed turning point problems with an interior layer[J].Journal of Computational and Applied Mathematics,2013,255:97-105.
[5]Cui M G,Lin Y Z.Nonlinear Numerical Analysis in Reproducing Kernel Space[M].New York:Nova Science Pub Inc,2009:15-50.
[6]Geng F Z,Cui M G.Solving a nonlinear system of second order boundary value problems[J].J Math Anal Appl,2007,327:1167-1181.
[7]Geng F Z,Cui M G.A novel method for solving a class of singularly perturbed boundary value problems based on reproducing ker⁃nel method[J].Appl Math Comput,2011,218:4211-4215.

