二阶中立型多时滞差分方程的振动性和渐近性
郑允利
(徐州生物工程职业技术学院 基础部,江苏 徐州 221006)
1 引言
由于计算机科学、生物数学、现代物理等自然科学与边缘科学的迅速发展,对时滞差分方程定性理论的研究近年来十分活跃.许多学者对二阶中立型时滞差分方程的振动性、渐近性及正解存在性作了探讨,取得了大量成果[1-7].但已有文献中所研究的方程大都是单时滞的,而从实际中抽取出来的数学模型通常是多时滞的.任荣霞、吴淑慧在文献[1]中研究了二阶不稳定中立型非线性差分方程
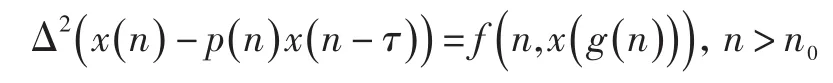
得到在p(n)的不同条件下及当g(n)<n时,该方程有界解振动的若干充分条件;邢海龙等在文献[5]中讨论了二阶中立型非线性多时滞差分方程n>n0.建立了该方程分别在和的条件下,每个有界解振动的充分条件.
在此基础上,下面将研究一类二阶中立型多时滞差分方程
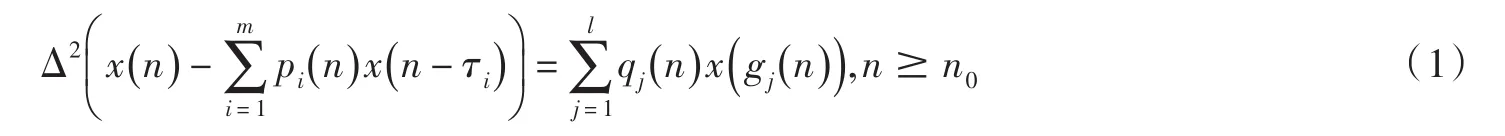
的振动性和渐近性,其中{ pi(n ) } 是非负实数序列,τi,i=1,2,...,m是非负整数,且存在非负整数τ,使得τ=max{τi, i=1,2,...,m} ; {qj( n ) } 为非负实数序列,gj:N0→N0,且j=1,2,...,l.令

2 预备知识
“ Δ”表示向前差分算子,即 Δ x(n)=x(n + 1)-x(n);Z表示所有整数构成的集合,设 a ∈Z,记N(a)={a , a+1,…},N=N(0).
一个差分方程的解{x ( n ) } 称为最终为正的,是指存在正整数M,使得n∈N(M ) 时,有 x (n)>0;若存在正整数M,使得n∈N(M ) 时,有 x (n ) <0,则称{x ( n ) } 最终为负的.
一个差分方程的解{x ( n ) } 振动,是指{x ( n ) } 既不最终为正,也不最终为负;否则,称之为非振动的.一个差分方程称为振动的,如果方程的所有解都是振动的.
引理2.1[7]假定i=1,2,…,m,且,若其中 | L |<∞,则存在,且等于
3 主要结果
定理3.1假定g()n<n,n≥n0,且下列条件成立
(H1)存在 p ∈[0 , 1) 使得;(H2)则方程(1)所有有界解振动.
证明设 x(n ) 是方程(1)的最终有界正解,则存在n1≥n0,当n≥n1时,有 x (n - τ)>0,x(gj( n ) ) >0.由方程(1)和(2)式得,当 n >n1时,有 Δ2z(n)>0,因此 Δ z(n)最终定号.如果 Δz(n)>0,则必有nl i→m∞z(n)=∞ ,这与z(n)有界矛盾,故Δz(n)≤0.从而z(n)严格单调下降,因而z(n)只能最终为正或最终为负.
若z(n ) 最终为负,即存在n2>n1,当n≥n2时,有 z (n ) <0.记1≤mia≤xm{x ( n - τi)}=x(n - τ),由(2)式和(H1)可知当 n ≥n2+kτ 时,有 x (n)<px(n - τ ) <pkx(n - kτ).由上式可得nl i→m∞x(n)=0,从而nl i→m∞z(n)=0,这与Δz(n)≤0且z(n)<0矛盾.
若z(n)最终为正,根据z(n ) 的性质,存在n2>n1,当n≥n2时

令 σ=g(n),μ=g(s) ,根据(3)式和方程(1)得

将(4)式两端关于 s 从 g (n)到n-1求和得
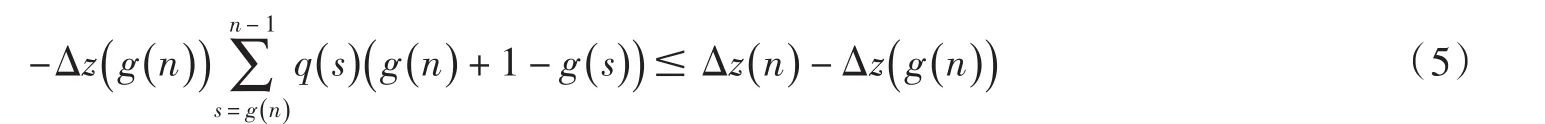
根据 Δz(n ) ≤0及(5)式得

即
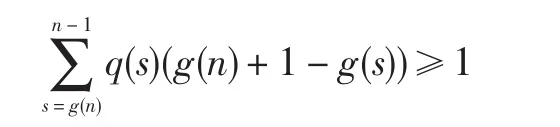
这与(H2)矛盾,故 z()n最终为正也不成立.证毕.
定理3.2假设下列条件成立
(H3)则方程(1)存在有界非振动解x(n)使得

当且仅当

证明假 定x(n ) 是方程(1)的最终有界正解且满足(6)式,则存在 n1≥n0,当 n ≥n1时,有 Δ2z(n)>0,Δz(n)≤0,从而lin

对(8)式两端从 s到 ∞求和,得

对(9)式两端从n到∞求和,得因为z()

n 有界,由(10)式可知(7)式成立.
下面假定(7)式成立.由(7)式可知,存在充分大的正整数N,使得

记Ω={x ∈ E:1≤x(n)≤2,n≥N-τ},则Ω是E的有界闭凸子集.定义算子T:Ω→E如下
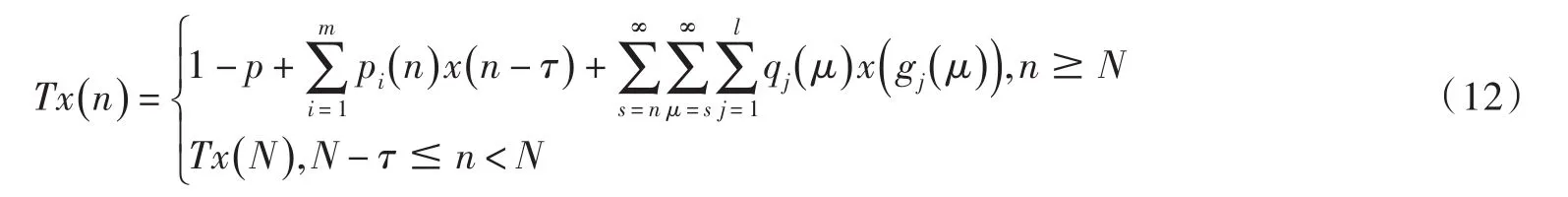
对任意的 x1,x2∈Ω ,当n≥N时,有
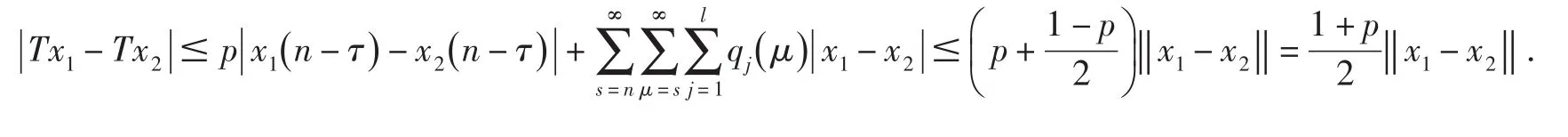
由此得
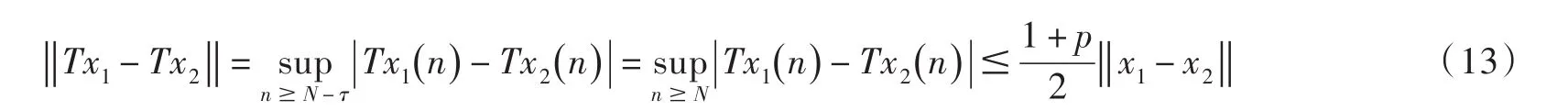
当 N-τ≤n<N时,对任意的 x1,x2∈Ω ,有(13)式成立.因为所以T为Ω上的压缩映射,也是连续算子.
对任意的x∈Ω ,当n≥N 时 ,由(11)式 和(12)式 ,得Tx(n)≥1-p+p=1.即1≤Tx(n)<2.
显然,当 N -τ≤n<N时,亦有1≤Tx(n)<2.因而,Tx∈Ω.即T为Ω上的自映射. 由Banach空间上的压缩映射原理可知,存在一个x∈Ω,使得Tx=x.由(12)式知,此不动点x满足
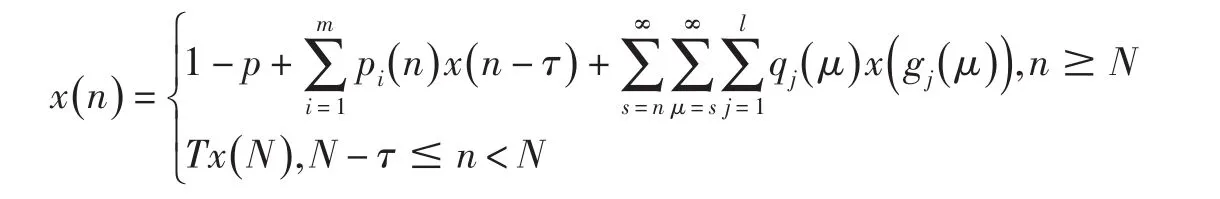
显然不动点x是方程(1)的一个有界正解且满足(6)式.
→m∞Δz(n)=0,nl→im∞z(n)=L≠0.
由方程(1)和(2)式及(H3)得
定理3.3…,m,且和

则方程(1)的有界非振动解渐近趋向于零.
证明假 设x(n)是方程(1)的最终有界正解,根据定理3.1的证明知,Δz(n)≤0,z(n)>0最终成立且
若L>0,则存在M>0使得x(n)>z(n)>M ,对方程(1)两边从 n0到 n-1求和,得

当x(n)为方程(1)的最终有界负解时,同理可证.证毕.
[1]任荣霞,吴淑慧.二阶不稳定中立型非线性差分方程有界解的振动性[J].河北师范大学学报:自然科学版,2002,26(2):118-122.
[2]Zhang Zhengguo,Biping,Dong Wenlei.Scillatory of unstable type second neutral difference equations[J].Korean J Comput Appl Math,2002,9(1):87-99.
[3]孙喜东,刘柏枫,刘晓辉.一类二阶中立型差分方程正解的渐近稳定性[J].数学的实践与认识,2009,39(17):217-220.
[4]郑允利,钟晓珠,张涛,等.二阶中立型差分方程非振动解的不存在性和渐近性[J].科学技术与工程,2007,7(21):5468-5470.
[5]杨甲山.二阶变系数多时滞非线性中立型差分方程的正解[J].四川师范大学学报:自然科学版,2009,32(4):470-473.
[6]邢海龙,钟晓珠,王东华,等.二阶中立型非线性多时滞差分方程有界解的振动性[J].燕山大学学报,2004,28(4):310-314.
[7]Zhou Yong,Zhang B G.The classification and existence of nonoscillatory solutions of second-order neutral delay difference equa⁃tions[J].ZAA(Anal Appl),2001,20(1):223-234.

