笛沙格的调和点列及其现实运用

浙江省宁波市北仑明港中学 甘大旺 (邮编：315806)

初数研究

笛沙格的调和点列及其现实运用

浙江省宁波市北仑明港中学 甘大旺 (邮编：315806)

从古希腊数学家阿波罗尼(奥)斯(P.Apollonius，约前262～约前190年)对圆锥曲线的研究成果中，可以窥见调和点列的雏形；在古希腊数学家梅涅劳斯(Menelaus，活跃于公元100年前后)、帕波斯(Pappus，活跃于公元300～350年间)探索到交比不变形的基础上，法国数学家笛沙格(G.Desargues,1591 ～ 1661)首次建构了圆锥曲线中调和点列的理论框架，并丰富了阿波罗尼(奥)斯的圆锥曲线的知识体系.本文以两个引例为基础，通俗地介绍调和点列的基本概念，然后着重解答和诠释以调和点列为命题背景的相关现实问题，供参考！

熟悉上述两个引例的结论后，我们就会认同笛沙格关于“调和点列”概念的自然性和必要性.

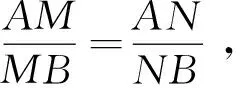
性质1 若共线四点A、M、B、N构成调和点列，则四点B、N、A、M也构成调和点列，四点M、A、N、B也构成调和点列，四点N、B、M、A也构成调和点列，四点A、N、B、M也构成调和点列.

命题专家以调和点列为题根，可以翻新编拟出相关的高考题、竞赛题.

例1 (2009年四川竞赛题)如图，已知PA、PB是⊙O的两条切线(A、B是切点)，PCD是⊙O的一条割线(C、D是交点)，E是AB与PD的交点．

证明 连结AC、AD、BC、BD，那么

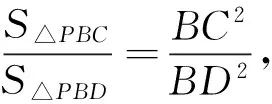
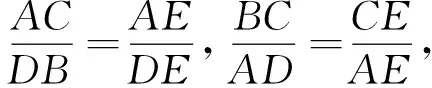
补注 在此例中，定点P与切点连线AB是关于⊙O相伴的极点与极线，此例把极点、极线与调和点列密切联系起来，可得到上述引例2的推广结论“过圆非切点的极点作直线与圆、极线相交，则所出现的四点顺次构成调和点列”.

(2) (2009年陕西竞赛题)已知PA、PB圆O的两条切线，切点分别为A、B，过点P的直线交圆O于C、D两点，交弦AB于点Q，求证：PQ2=PC·PD-QC·QD.

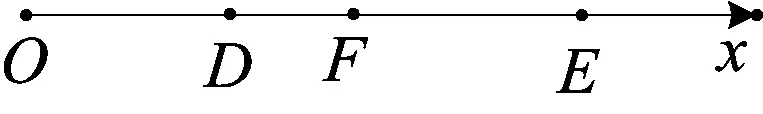
(2)如下左图，以P为原点建立一维数轴Px，则P(0)，设C(c)、Q(q)、D(d)，则与(1)同理得2cd=q(c+d).于是，PC·PD-QC·QD=cd-(q-c)(d-q)=2cd-q(c+d)+q2=PQ2，证毕.

(3)如上右图，以A为原点建立一维数轴Ax，则A(0)，设B(b)、P(p)、C(c)，则与(1)同理得2bc=p(b+c)，则

AP·BC-2PC·AB=p(c-b)-2(c-p)b=p(b+c)-2bc=0，

则AP·BC=2PC·AB.

最后两边除以BC·PC，得到原等式正确.

补注 本例的3个小题结论的形态不同，但它们都是例1结论的必要条件，读者还可以反推它们也是例1结论的充分条件.于是，我们可以得到下面的性质.

⟺AB2=AM·AN-BM·BN.

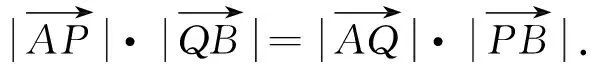
将两点A(x1,y1)、B(x2，y2)的坐标代入椭圆C的方程x2+2y2=4，并整理得

相减得8λ(2x0+y0-2)=0(其中λ>1)，

则 2x0+y0-2=0.

所以，点Q总在定直线2x+y-2=0上.

补注 如右图，目标直线2x+y-2=0恰恰是题设定点P(4，1)关于已知椭圆C：x2+2y2=4的极线(即过椭圆C外一点P向该椭圆所作两条切线的两个切点的连线)，这说明例1、例2的结论的逆命题可以类比到椭圆来探究.

例4 (2014年河南竞赛题)已知抛物线C：x2=2y与直线l：y=kx-1没有公共点，设点P为定直线l上的动点，过P作抛物线C的两条切线，其中A、B为切点.

(1)证明：直线AB恒过定点Q;

解 (1)设A(x1,y1)，则x12=2y1．运用判别式法或导数法求得抛物线在A点处的切线方程为y+y1=x1x.设P(x0,kx0-1)，则代入得

(kx0-1)+y1=x0x1.

设B(x2,y2)，同理有kx0-1+y2=x0x2. 于是，两切点连线AB的方程为

kx0-1+y=x0x，化成直线系方程为

设M(x3,y3)、N(x4,y4)，则

⇐2x3x4+2kx0=(k+x0)(x3+x4)

⇐2[(2k2-2)x0-2k]+2kx0(x0-k)

=(k+x0)(2kx0-4)

⇐0=0.

因为此等式显然正确，故原等式正确.证毕.

补注 ①根据极点(线)的结论，可以直接写出切点连线AB的方程为x0x=y+(kx0-1)，其实，点P与连线AB是关于抛物线x2=2y相伴的极点与极线，点Q与直线l也是关于抛物线x2=2y相伴的极点与极线；②第(2)小题说明四点P、M、Q、N四点构成调和点列.

综上四例，你能顿悟下面一个推广结论吗？

定理1 如果经过定点P可以向圆锥曲线Ω作两条切线，切点分别是T1、T2，再经过定点P作动直线l与圆锥曲线Ω相交于两点A、B．

(1)当动直线l与连线T1T2相交于点Q(不重合于T1、T2两点)时，顺次四点P、A、Q、B构成调和点列；

(2)当动直线l上的点Q使得顺次四点P、A、Q、B构成调和点列时，点Q在连线T1T2上(不重合于T1、T2两点).

限于篇幅，把定理1的验证留给读者完成.因势利导，下面介绍笛沙格的一个研究成果.

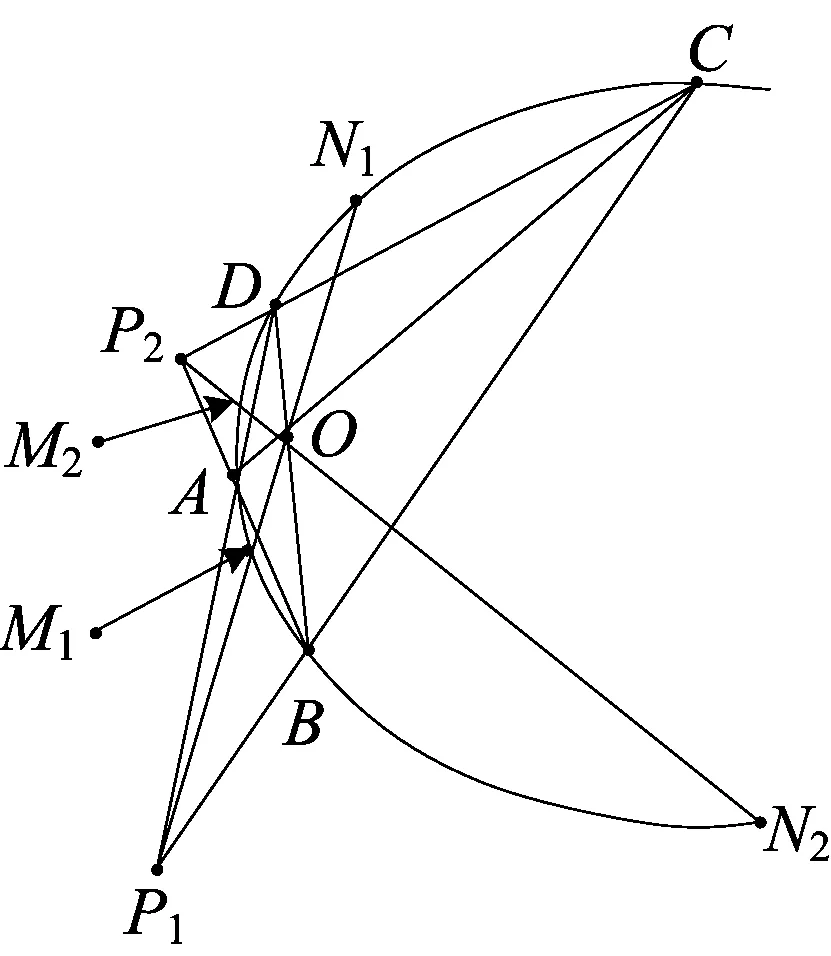
定理2 如果圆锥曲线Ω的内接四边形ABCD的两条对边AD与BC的延长线交于点P1，另两条对边AB与CD的延长线交于点P2，且圆锥曲线Ω与其割线P1O交于两点M1、N1，圆锥曲线Ω与其割线P2O交于两点M2、N2(如上图)，那么内接四边形ABCD的两条对角线相交于O点的充分必要条件是顺次四点P1、M1、O、N1构成调和点列，且顺次四点P2、M2、O、N2也构成调和点列.

用极限的思想琢磨，定理1是定理2的退化情形.近几年来以定理1为背景，是专家编拟高考题、竞赛题的热点；预计以定理2的特例为背景，可能是专家在不远的将来编拟高考题、竞赛题的新热点.

1 李文林. 数学史概论[M].北京：高等教育出版社，2002：133-134

2 傅海伦.中外数学史概论[M].北京：科学出版社，2007：234-235

3 傅钟鹏.数学名人漫记[M].天津：新蕾出版社，2001：43-45

4 杜瑞芝主编.数学史辞典[M].济南：山东教育出版社，2002：100,423

2014-12-28)