一道向量试题的探究和思考
2015-06-15 19:16:38安徽省枞阳县宏实中学江保兵邮编246700
中学数学教学 2015年3期
安徽省枞阳县宏实中学 江保兵 (邮编:246700)
一道向量试题的探究和思考
安徽省枞阳县宏实中学 江保兵 (邮编:246700)
1 试题及解法
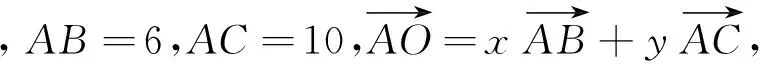

将AB=6,AC=10代入上面的两个式子中,化简得:
6x+10cos∠BAC·y=3,6cos∠BAC·x+10y=5 ,又2x+10y=5,三式联立解得:



①
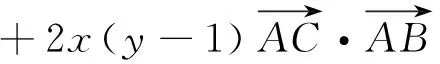
②
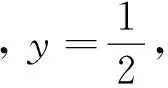

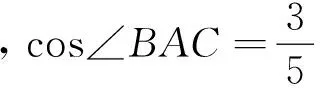
2 试题推广


即 2c2x+2bccosA·y=c2
①
2bccosA·x+2b2y=b2
②
解这个二元一次方程组,并由正余弦定理得:
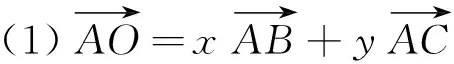
这是我们在各种考试中经常见到的一种形式,例如下面这道试题就是以⑶为背景来命制的.
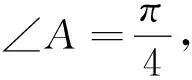
3 类比推广

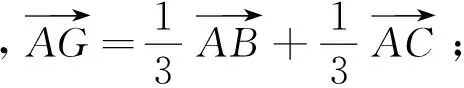


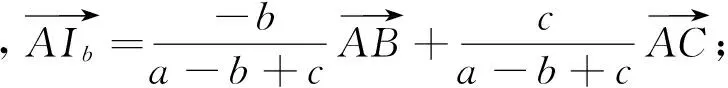
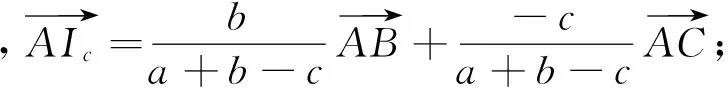
(4)当H为△ABC的垂心时,



证明 (1)、(2)证明比较简单,留给读者.这里主要给出(3)和(4)的证明.
(3)当Ia为△ABC中∠A所对的旁心时,过Ia作BC的平行线交BC的延长线于B1、C1.设BB1=ct,则IaB1=ct,IaC1=CC1=bt,如图所示.

①.
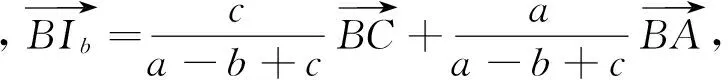
所以
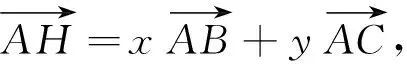
c2x+bccosA·y=bccosA
①
bccosA·x+b2y=bccosA
②
解这个二元一次方程组,并由正余弦定理得:

当△ABC为非直角三角形时,


4 一个熟悉的结论
由上面的讨论,我们自然而然地得到以下结论.
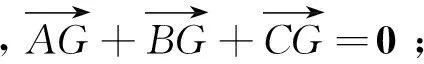
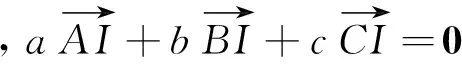

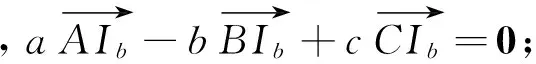
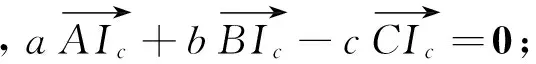
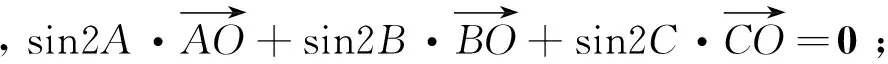
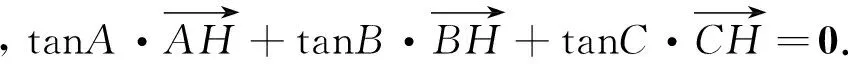
1 江保兵.平面向量的共线定理及其推论[J].中学数学研究(广州),2014,( 3)
2 李金聪.三角形“五心”优美的向量形式[J].福建中学数学,2010 ,( 3)
3 贺功保,叶美健.三角形的五心[M].哈尔滨:哈尔滨工业大学出版社,2009
2014-12-21)
猜你喜欢
党员生活·下(2022年2期)2022-04-23 13:48:03
速读·下旬(2022年1期)2022-04-09 22:18:34
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14 07:36:32
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27 03:04:28
河北理科教学研究(2020年1期)2020-07-24 08:14:28
当代陕西(2019年24期)2020-01-18 09:14:58
中国科技博览(2017年25期)2017-08-09 20:15:29
智富时代(2017年4期)2017-04-27 02:13:48
安徽农学通报(2015年11期)2015-06-22 11:19:19
安徽农学通报(2015年10期)2015-06-15 01:13:54

