巧解幽隐无穷事 探源究本方顺理
——对一道“独立事件”问题的解法探究有感
浙江省象山中学 杨育池 (邮编:315700)
巧解幽隐无穷事 探源究本方顺理
——对一道“独立事件”问题的解法探究有感
浙江省象山中学 杨育池 (邮编:315700)
微课以视频为表现方式,记录教师在教学过程中,围绕教学中的重点、难点与疑点知识或问题而开展的教与学的活动过程,是数字化教与学资源中的一种.留心身边,笔者发现我们平时的答疑解惑、辅导讨论活动也短小精干,虽不能通过网络传播,但更具生成性与互动性,是极真实、极具可视可评性的“微课”.
1 同题不同构,巧解幽隐无穷事
学科辅导时间,我校两位青年教师差不多在同一时间、围绕同一问题为学生展开教学答疑,向笔者展示了一次简短而精彩、完整且精致的同题异构“微课”.
例1 一名工人要看管三台机床,在一小时内机床不需要工人照顾的概率对于第一台是0.9,第二台是0.8,第三台是0.85,求在一小时的过程中不需要工人照顾的机床台数X的数学期望(均值).
1.1 析理不透难解惑
甲班一同学问L老师:您上课时讲了这个题的解法,我发现有巧妙的算法:E(X)=0.9+0.8+0.85=2.55台.
L老师:嗯,不错,真巧,会不会是巧合呢?
学生:我用其它数据也验算了这种算法,所得期望值还是一样.
L老师:看来这不是巧合了.我们来验证一下吧.
L老师用字母代替具体数字将问题“一般化”:一个工人看管三台机床,在一小时内,这三台机床需要工人照管的概率分别为p1,p2,p3,求在一小时内不需要工人照管的机床台数X的数学期望.
师生共同验证:记“第一台,第二台,第三台机床不需照顾”分别为事件A,B,C.又随机变量X的可能取值为0,1,2,3.由独立事件的概率公式与对立事件的概率公式,得
P(X=3)=P(ABC)=p1p2p3.
因此,由离散型随机事件的数学期望公式,得E(X)=0·P(X=0)+1·P(X=1)+2·P(X=2)+3·P(X=3)=p1+p2+p3.
L老师:是正确的,看来你的数学感觉很好!你给出的这个结果应该有很多的应用.
L老师用几个具体问题佐证自己的论断,并与学生大谈“二项分布”与此结果的关系,向学生指出:二项分布适用于n次独立重复试验,此结论适用于n次可重复或不重复的独立试验.并认为独立重复试验只是独立试验的一种特殊情形,因其特殊性,所以具有特殊的研究价值.而对于一般的n次独立试验,有其统计方面的方法,但是因其过于灵动,规律特征不明显,我们才不予以系统研究.
静心细听了L老师的释疑解惑,看着学生离开办公室,笔者心中却泛起更多的问号:教师是否为学生解释清楚了疑问,解法为什么对?正确性根源在哪里?碰巧,过了一天,乙班的一名同学也向其任课教师G老师请教此题.于是笔者又留意起“师生对话”.
1.2 探源究本显其理
学生:老师,这道题还可以按期望等于三台机床不需要照顾的概率之和来计算.
G老师:你真善于动脑筋!我想请你告诉我,这样算的道理是什么呢?
学生:从概率的角度看,一小时内第一台机床平均0.9台不需照顾,同理,第二台与第三台机床分别有0.8台和0.85台不需照顾.
G老师(赞赏):这是对概率的直觉认识,能否给出更科学合理的解释?来,我们研究一下.
G老师:记“第一台机床不需照顾”分别为事件A,“第二台机床不需照顾”为事件B,第“三台机床不需照顾”为事件C.则事件A、B、C有什么关系?
学生:它们为相互独立事件.
G老师:在一小时内机床不需要工人照管的试验可以看作一次随机试验,这就是我们利用数学期望的定义解题的出发点;它也可以看作针对事件A、B、C分别作一次随机试验,那么事件A、B、C有何性质呢?
学生(恍然大悟):哦,每一次试验中,“不需要照顾”要么发生,要么不发生,那就是它们对应的随机变量服从两点分布.您的意思是,将一小时内不需要工人照管的机床所对应的随机变量X分解成三个随机变量,即X=aX1+bX2+cX3,根据随机变量的均值的线性性质E(X)=E(aX1+bX2+cX3)=aE(X1)+bE(X2)+cE(X3)求解.
G老师:你很聪明!对不具独立性的几个随机变量,这个结论仍成立.这样,把一个比较复杂的随机变量分解成几个背景简单的随机变量之和,通过数学期望的性质求复杂随机变量的数学期望的方法,它具有一定的普遍意义,是概率论中常用的一种方法.使用得当,可使复杂问题简单化.你解题时不自觉地在化繁为简.
学生:懂了!因为事件A、B、C所对应的随机变量X1、X2、X3均服从两点分布,且P(X1)=p1、P(X2)=p2、P(X3)=p3,所以
E(X)=E(X1+X2+X3)=E(X1)+E(X2)+E(X3)=p1+p2+p3=2.55台.
学生(追问):这种方法真巧妙!不知道是否适用于复杂事件的数学期望与方差计算呢?
G老师:你的思考还比较深入嘛,还是试试吧.我们先看看特殊的分布.
故ξi~(0,1)分布,且A发生的次数ξ=ξ1+ξ2+…+ξn服从二项分布.由于ξ1、ξ2、…、ξn相互独立且同分布,这样二项分布B(n,p)可看作由n个服从(0—1)分布的随机变量组成.因此,由数学期望的线性性质,有Eξ=Eξ1+Eξ2+…+Eξn=np.
学生:推导二项分布的数学期望可以这样啊!原来两点分布既是二项分布的特殊情形,也是二项分布的有机构成部分.
G老师:那你知道如何去求二项分布的方差了吧?
学生:让我按照您刚才的思路来试试.随机变量ξ的方差Dξ,反映的是ξ的取值偏离于均值的平均程度,实际也是随机变量ξ的函数(ξ-Eξ)2的数学期望E(ξ-Eξ)2.
对于随机变量ξ、η,当Dξ、Dη存在时,有
D(ξ+η)=E(ξ+η)2-[E(ξ+η)]2
=E(ξ+η)2-(Eξ+Eη)2
=Eξ2+Eη2+2E(ξη)-(Eξ)2-(Eη)2-2Eξ·Eη=Dξ+Dη+2[E(ξη)-Eξ·Eη].方差好象不具有线性性质.
G老师:如果方差要具有线性性质,必须满足什么性质呢?
学生:必须E(ξη)=Eξ·Eη,应该是ξ、η为相互独立的随机变量!
G老师:很好!请接着求二项分布的方差.
学生:我知道若随机变量η服从两点分布,则Dη=p(1-p)=pq.由此,若ξ~B(n,p),且ξ=ξ1+ξ2+…+ξn,由于ξ1、ξ2、…、ξn为n个服从(0-1)分布的随机变量,所以Dξ=D(ξ1+ξ2+…+ξn)=Dξ1+Dξ2+…+Dξn=npq.看来对于一般的独立试验,也能利用这种方法处理.
G老师:太好了!你很善于思考,已经较深刻理解两点分布与二项分布之间的内在联系.下面实践来检验你的方法.

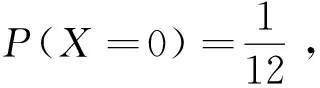
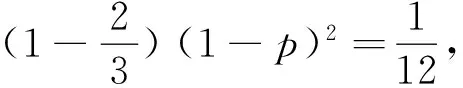
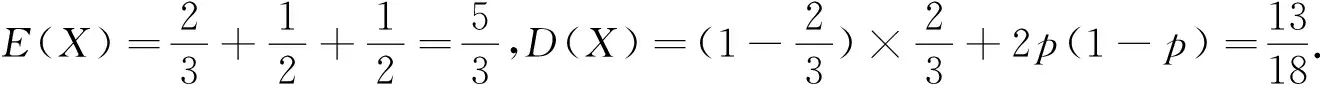
例3(2012年浙江理科第19题改编) 已知箱中装有4个白球和5个黑球,且规定:取出一个白球得2分,取出一个黑球得1分,现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出3球所得分数之和.求X的数学期望E(X)与方差D(X).


学生(自言自语):无放回取球?这是超几何分布问题.前后的可能性会有影响啊,这样ξi并不独立了!如果是有放回取球,二项分布就好办了.

学生:我就是这么想的,因为数学期望对不相互独立的随机变量仍具有线性性质,但……
G老师:在超几何分布中,ξi同分布但不相互独立,就应回到方差的定义求D(ξ).

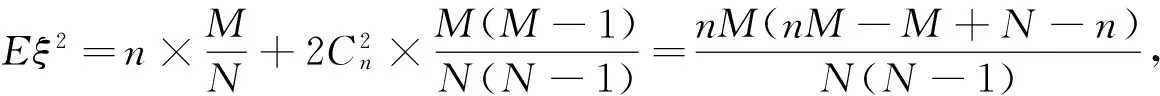
所以D(ξ)=Eξ2-(Eξ)2=
学生:好象有点明白了.老师,此题中由于X=(ξ1+1)+(ξ2+1)+(ξ3+1),由您刚才的方法,有D(X)=E(X2)-[E(X)]2
将一个复杂的随机变量分解为简单的随机变量之和是多么巧妙而富有艺术的一招!这类问题我真懂了!
2 课微情怀异,教者有道生受益
这是典型的“同题异构”微课教学,网络上录制的教学视频无论多么精彩,与笔者身居现场感受师生面对面教学的热烈交流与对话互动,还是有一定的距离感.两位老师面对相同的教学资源,运用的教学策略类似,“异构”了问题研究与处理方式,凸显的是教师个体专业知识结构与教学理念的差异,而笔者则欣赏到思想碰撞和心灵交流的曼妙乐曲,不禁有些感慨.
数学理解的基础是教师自身数学知识的结构化、网络化和丰富联系,顾泠沅教授指出,卓有成效的教学常常基于教师对学科知识的通透理解.确定一个方法是否正确,能否推广需要教师有良好的思维习惯与敏锐的数学洞察能力,更需要深厚的专业知识修养.一个对知识本质知之不多的教师,又怎么能促进学生的发展和成长,实现数学的本质与教育价值?
L老师在答疑过程中,以问题为“源头”,引导学生经历质疑——一般化——理论总结等几个思维环节,看似有利于学生形成一种连续的研究学习思路,但从数学知识的整体性与联系性角度看,由于教师缺乏从概率论的学科整体上把握知识的联系的能力,学生仍未看到知识的发生发展,无法形成系统的知识网络,因而疑问仍旧存在.这样计算虽是必然,但其必然性如何正确解释?答疑的尾声,L老师反而纠缠于此结论与二项分布的关系,看似非常“高大上”的回答,恰恰说明教师未能理解相关数学知识的来龙去脉,在“答非所问”.学生长期在这种“似是实非”的教学下学习,即使教师有再丰富的教学经验,能再娴熟地运用“产婆术”,最终学生增长的只是解题的“知识”,头脑中“没有清晰的数学概念,对定理不甚了了,只是做题的机器”;学生于数学学习,也只是在错误的方向上坚持、努力.
G教师在师生对话交流中,及时抓住知识的连接点、生长点,寻找问题“巧解”下隐藏着的知识联系;引导学生认识知识的多向与深层的联系性,帮助学生将朴素直觉认识上升为理论,有利于学生数学知识的系统化;通过解法合理性的讨论,有机融合合情推理与演绎推理,努力挖掘知识的相关性和相通性,使学生经历“问题—探究—发现—推广”的思维过程,学生在这种淡墨无痕的教学浸润中,对数学知识与方法的运用既“知其然”又“知其所以然”,思维能力一定能提高,学习兴趣会激发.这样的数学教学才是我们应当追寻的,因为具体的知识学习多年后会逐渐忘记,但是研究问题的方法和思路一旦领会就终身难忘,这就是数学教育给予学生的长远影响.
同时,笔者从两位老师的答疑活动中,深切感受到“教什么”比“怎么教”重要,数学教学的本质是教学生学习数学学科的内在逻辑与数学独特的文化价值.理解数学学科的研究方法和思路,掌握具体的数学学科知识比“怎么教”更重要.优秀的数学教师,能教给学生数学的“本质”——把握数学的经验化和演绎化的统一;教给学生数学的“过程”——把数学知识“冰冷的美丽”恢复为“火热的思考”;教给学生数学的“思想”与“结构”——通过数学知识的探索,使学生体验数学的思想方法与理性精神,有助于“数学头脑”的养成.
因而,一名优秀的数学教师应具备扎实的数学专业基础,把握数学学科知识、核心思想及教育价值,明晰数学知识和方法的源与流,这样在理解数学的基础上才能理解学生、理解教学.
1 刘绍学主编.普通高中课程标准实验教科书数学(选修2-3,A版)[M].北京:人民教育出版社,2009年4月第3版
2 章建跃.编后漫谈:课堂教学要注重数学的整体性[J].中小学数学(高中版), 2013(5)
2014-12-25)

