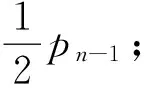如何探寻递推关系
江苏南通市南通建筑职业技术学校 杨 忠 (邮编:226000)
走进新课程
如何探寻递推关系
江苏南通市南通建筑职业技术学校 杨 忠 (邮编:226000)
概率、排列和数列都是高中数学的重要内容,由于三者之间存在内在关联性,在近几年的高考、自主招生等各类考试中经常出现三者交汇题.此类题目以某个实际问题为背景,以概率或组合问题的形式呈现,需要学生首先找到某项与前几项之间的递归关系,再由求数列通项公式的方法和手段求解.在实际教学中,笔者注意到解决此类问题时,由递推数列求解通项数列属于程序性知识和方法,对学生而言不是难点.学生困难之处在于怎样从实际问题出发,经过分析建立数学模型,即确定问题中存在的递推关系,这也是数学教学中的一个薄弱点.笔者就这个问题,谈谈思考和心得.
首先以著名的结草成环问题为例来说明.
例1 现有n(n∈N*)根草,共有2n个草头,现将2n个草头平均分成n组,每两个草头打结,求打结后所有草能构成一个圆环的打结方法数.
解析 递推关系pn=f(pn-1,pn-2,…,pn-k)本质是由pn之前若干项表示出来,所以分析问题时首先应明确目标pn为哪个量,pn-1,pn-2,…,pn-k又相应是什么量.
这个问题中,将n根草打结后所有草能构成一个圆环的打结方法数记为pn,那么将n-1,n-2,…,1根草打结后所有草能构成一个圆环的打结方法数依次记为pn-1,pn-2,…,p1.
如何求pn,可以先假设pn-1,pn-2,…,p1是已知或已经求得,若有需要这n-1个量都可以用来表示pn,然后考虑如何实现pn对应的状态向pn-1,pn-2,…,p1对应的状态转移.
本题中,即考虑如何将pn对应的n根草状态向n-1根草状态转移,将草头编号为1、2、3、……、2n-1、2n.不失一般性,先考虑1号的打结,1号和2号头打结不合题意,1号和3、…、2n-1、2n共有2n-2个草头可以打结,所以有2n-2个打法.然后考虑剩余草头2n-2个,此时可以看成n-1根草打结后所有草能构成一个圆环情形,其方法数为pn-1,这样由分步原理知递推关系为pn=(2n-2)pn-1,易得p1=1.

1 直接转移法
将n情形下状态转移为n-1情形下的相同状态,如例1.现再举一例.

图1

解析 记M1 将n情形下状态转移为排除n-1情形下的相应状态. 图2 用这个结论解2003年高考江苏卷:某城市在中心广场建一个花圃,花圃分为6个部分如图3,现要栽种4种不同颜色的花且相邻部分不能同色,由不同的栽种方法有____种. 图3 只需将图变形为圆环形,1区有4种栽法.不同的栽法数为 N=4a5=120. 例4(2012全国高中数学联赛 8) 某情报站有A、B、C、D四种互不相同的密码,每周使用其中的一种密码,且每周都是从上周未使用的三种密码中等可能地随机选用一种.设第一周使用A种密码,那么第7周也使用A种密码的概率是______(用最简分数表示). 解析 本题与A、B、C、D四人之间传球问题具有相同的数学模型. 将n情形下状态转移为n-1情形下的若干不同状态,分类讨论. 例5A、B两人拿两颗骰子做抛掷游戏,规则如下:若掷出的点数之和为3的倍数时,则由原掷骰子的人继续掷;若掷出的点数不是3的倍数时,由对方接着掷.第一次由A开始掷,求第n次由A掷的概率. 解析 设第n次由A掷的概率为pn,第n-1次由A掷的概率为pn-1. 第n次由A掷转化为第n-1次由A掷和由B掷两种情形, 有时,需将n情形下状态转移为n-1、n-2、n-3、…若干阶段情形下的若干不同状态,分类讨论,如下题: 例6(2011年华约自主招生试题) 有一枚均匀的硬币连续抛掷n次,以pn表示未出现连续3次正面的概率. (1)求p1、p2、p3和p4; (3)略. 图4 解析 这里研究(2),pn表示抛掷n次连续3次来出现正面的概率,则pn-1表示抛掷n-1次连续3次来出现正面的概率,pn-2表示抛掷n-2次连续3次出现正面的概率,……依次类推,考察n,n-1,n-2,三个阶段的状态如图4,n次未出现连续3次正面不可能转化为①; 2015-03-30)
2 排除转移法



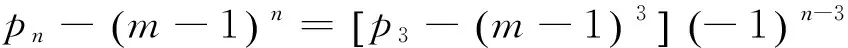

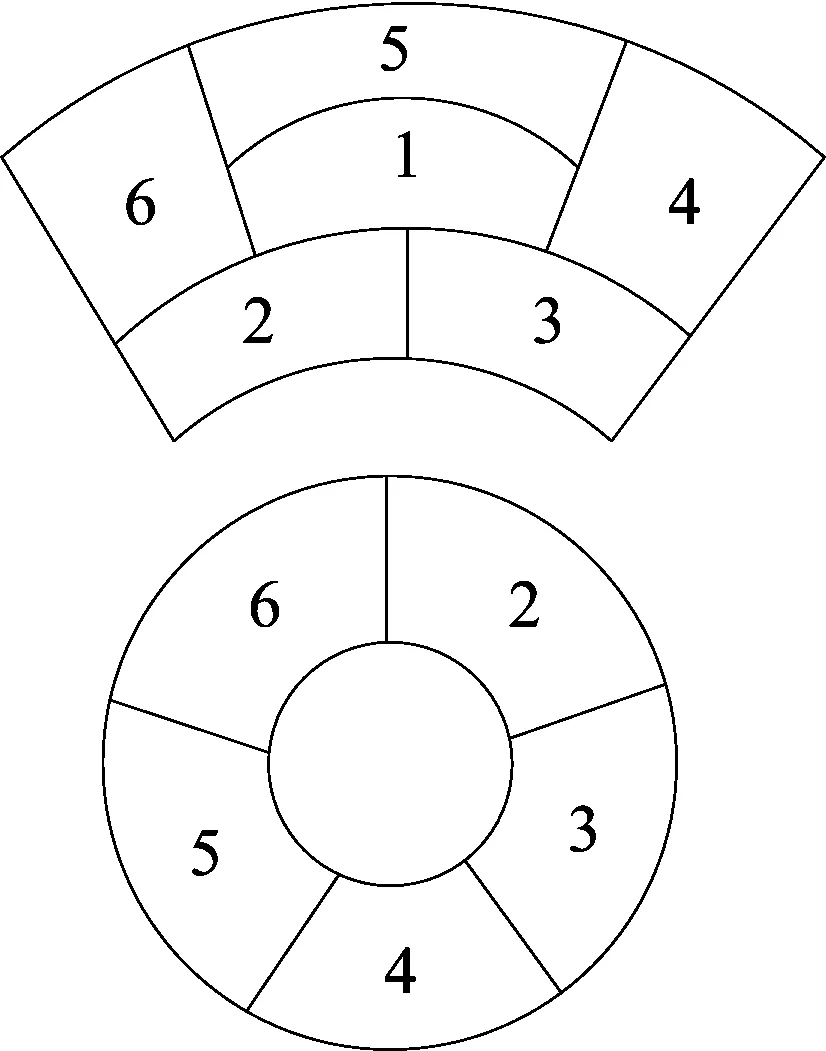

3 分类转移法