典型谱峭图在共振解调方法中的应用*

马新娜，杨绍普

(1.石家庄铁道大学信息科学与技术学院 石家庄，050043) (2.石家庄铁道大学机械工程学院 石家庄，050043)



典型谱峭图在共振解调方法中的应用*

马新娜1，杨绍普2

(1.石家庄铁道大学信息科学与技术学院 石家庄，050043) (2.石家庄铁道大学机械工程学院 石家庄，050043)

结合铁路货车滚动轴承检测中的常见典型故障，根据谱峭度法中峭度值最大化原则和工程实际中的快速精准需求，提出了一种典型谱峭图算法。将此方法用于共振解调技术中带通滤波器的中心频率和带宽参数的自动选取，形成基于典型谱峭图的共振解调方法。在货车滚动轴承实验台上对自然形成的故障轴承进行多次振动测试实验。将基于典型谱峭图的共振解调方法应用到实测振动信号的故障诊断分析中，并与基于快速峭度图的共振解调方法进行对比，结果验证了该方法能更有效地检测到货车滚动轴承中的故障并能诊断出故障类型。

典型谱峭图; 共振解调; 故障诊断; 滚动轴承

引 言

广泛应用于机械装备中的滚动轴承，往往处于恶劣的运行环境中，存在结构复杂、承受重载、运行速度高和容易发生故障的特点。轴承故障直接影响到安全生产和经济效益[1]。利用振动信号进行故障诊断的研究方法最多[2]，其中，共振解调技术利用故障产生的频率信号与系统本身固有的振荡频率相同时会产生共振的原理，通过放大和分离故障特征信号，可以比较准确地判断早期微弱故障的严重程度和损伤部位。共振解调技术因较高的信噪比和准确的早期故障诊断，得到了广泛关注[3]。传统的共振解调技术需要预先确定带通滤波器的中心频率和滤波带宽，无法适应轴承应用环境的变化和多样性，大大局限了在工程中的应用[4-5]。采用快速峭度图方法寻求的特征频率过大，得到带宽过宽，导致中心频率和滤波带宽精准性差[6]。Protugram方法确定的带通滤波器的带宽是固定的，在工程应用中存在局限性[7]。因此，研究中心频率和滤波带宽的自动准确选取对于共振解调在轴承故障诊断的工程应用具有重要意义。

根据轴承的故障特征频率和振动信号的峭度特征，结合轴承检测中的常见典型故障，提出典型谱峭图算法用于确定中心频率和带宽。该方法根据典型故障的特征频率有针对性的自动选择滤波带宽，寻求精确的中心频率，弥补了传统共振解调方法需要人工干预带通滤波参数的不足，并用实验结果验证了该方法的有效性，具有一定工程应用价值。

1 典型谱峭图算法

1.1 谱峭度

峭度对冲击信号敏感，适用于考察轴承系统中振动冲击的强弱。谱峭度(spectral kurtosis，简称SK)思想由Dwyer提出，其要求计算出与每个频率对应的峭度值从而得到瞬态的频带，弥补了传统功率谱不能准确检测信号中瞬态特征的缺陷[8-9]。Antoni将谱峭度作为短时傅里叶变换的窗口宽度函数，提出峭度图的概念[10-11]，并在此基础上，提出快速峭度图以缩减计算时间[12]，提高了在工程故障诊断中的应用价值。

关于谱峭度的数学描述认为，不平稳振动信号的激励响应[13]表示为

(1)

其中：H(t,f)为系统的传递函数，表示信号X(t)的激励响应Y(t)在频率f处的复包络。

Y(t)的四阶谱累积量描述为

(2)

其中：S(f)为谱瞬时距，用以表示包络能量大小。

(3)

信号Y(t)的谱峭度定义为

(4)

在滚动轴承故障早期，引起周期性冲击的振动信号比较弱，直接从频谱中识别低频故障特征频率存在困难。谱峭度对具有瞬态冲击类故障比较敏感，尤其是在故障早期表现明显。谱峭值的大小与中心频率和频率带宽的选择有直接关系，能否快速确定一个中心频率和带宽的最佳组合使谱峭度值最大，是依据谱峭值诊断轴承故障的关键。滚动轴承的故障类型不同，最大峭度频谱的中心频率也不同。

1.2 典型谱峭图算法

虽然不同滚动轴承所处的应用环境不同，但对于具体某一类机械上的滚动轴承来说，发生故障的种类及原因基本相同。在轴承故障检测过程中，偏重于经验积累下来的几种典型故障的检测。在谱峭度基础上，结合实际轴承检测中的典型故障，提出了典型谱峭图思想。考虑到区间划分过大失去精准性，过小无法体现故障的倍频特征，因此，典型谱峭图思想将轴承常见典型故障作为参考对象，分别按每种典型故障频率对振动信号的频谱区间进行划分。区间划分方法如图1所示。

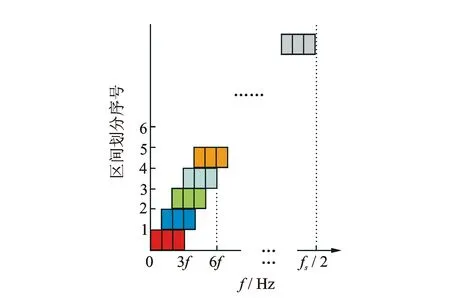
图1 区间划分

图1中f为典型故障频率，fs为采样频率。因为频谱中存在3次谐波时对应的峭度值最大，选定每个区间的带宽为3倍故障特征频率。中心频率的迭代步长选取1倍故障特征频率。第1个区间为0至3倍故障频率，中心频率为1.5倍故障频率；第2个区间为1倍故障特征频率至4倍故障特征频率，中心频率为2.5倍故障特征频率。以此类推，区间重叠。

求每个区间的峭度，形成某一种典型故障为参考对象的峭度曲线。分别针对每种典型故障进行区间划分，求峭度曲线。综合考虑各种故障类型的谱峭度曲线，找出谱峭度最大的带宽和中心频率，形成典型谱峭图算法，具体流程如图2所示。

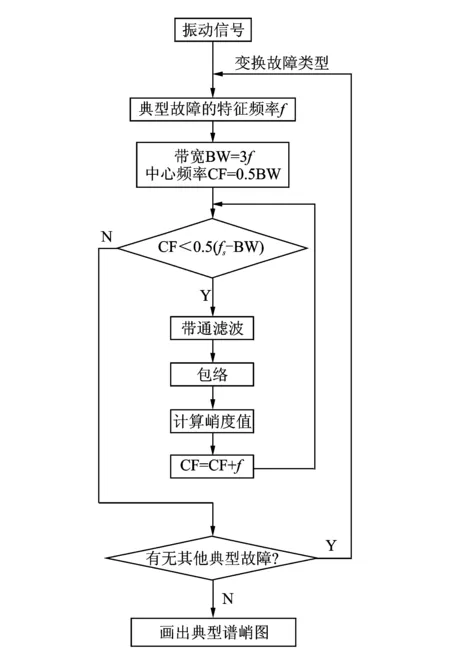
图2 典型谱峭图算法

2 基于典型谱峭图的共振解调方法

将典型谱峭图算法应用于共振解调技术中，形成基于典型谱峭图的共振解调方法，如图3所示。

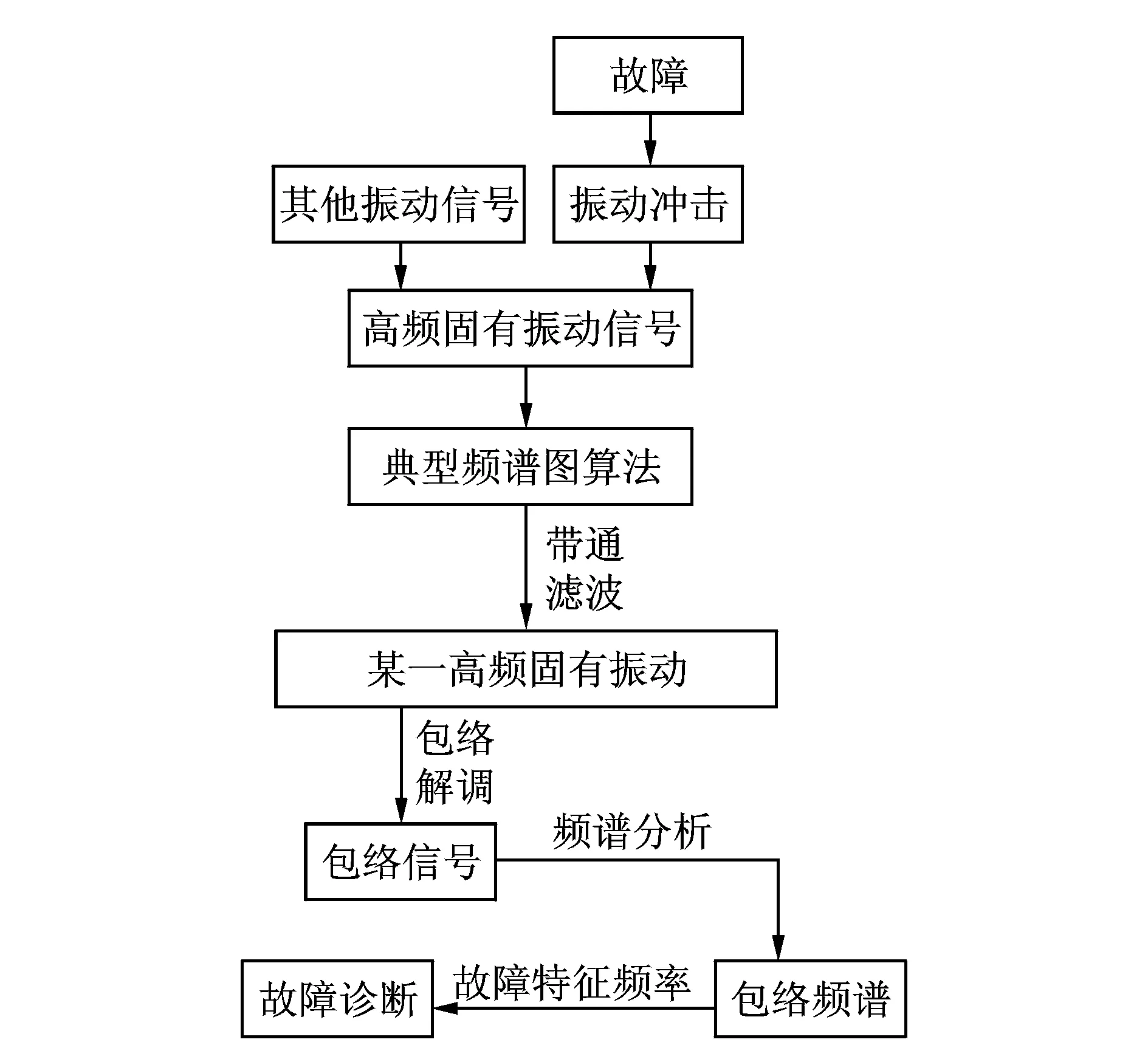
图3 基于典型谱峭图的共振解调方法

对采集的高频固有振动信号进行典型谱峭图算法分析，得到谱峭度指标最大的中心频率和带宽。将得到的中心频率和带宽作为共振解调中带通滤波器的参数，从而把高频固有振动信号分离出来。对经过带通滤波后的共振信号进行包络检波，得到与故障冲击频率一致的脉冲。然后，利用低通滤波器去除包络检波后信号中的高频干扰噪声，保留较低频率的故障信号成分。对包含故障信号的低频成分进行谱分析，识别故障特征频率。通过故障特征频率判断轴承故障的部位及程度。

3 实例验证

将基于典型谱峭图的共振解调方法应用于铁路货车轮对滚动轴承的故障诊断。铁路货车轮对滚动轴承故障诊断实验台如图4所示。

图4 故障诊断实验台

以我国60 t级铁路货车普遍使用的RD2197726型轮对滚动轴承为研究对象。实验所用轴承的故障为货车经过长时间运行后形成的自然故障，除了明显的滚动体故障外，轴承表面存在微小划痕。轴承主要结构参数如表1所示。

表1 滚动轴承的结构参数

根据滚动轴承参数可以求得轴承外圈、内圈和滚动体的故障特征频率。货车轴承故障诊断实验的主要工况及轴承故障特征频率如表2所示。

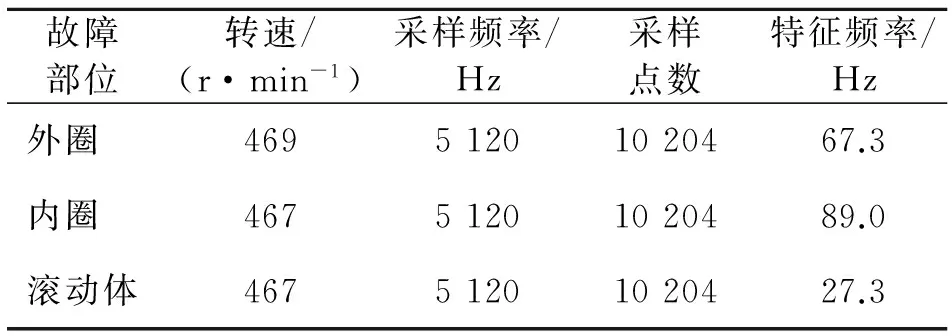
表2 实验工况

对有滚动体故障的轴承进行多次振动测试，采集轴承垂向振动信号数据进行分析。振动信号的部分时域数据如图5所示。

图5 滚动体故障振动信号时域图

铁路货车滚动轴承的典型故障为外圈、内圈和滚动体故障。利用典型谱峭图算法对采集到的振动信号进行分析。为了便于对比，同时用快速峭度图方法进行分析，寻求最大峭度值处的中心频率和带宽。得到快速峭度图和典型谱峭图后进行比较，如图6所示。

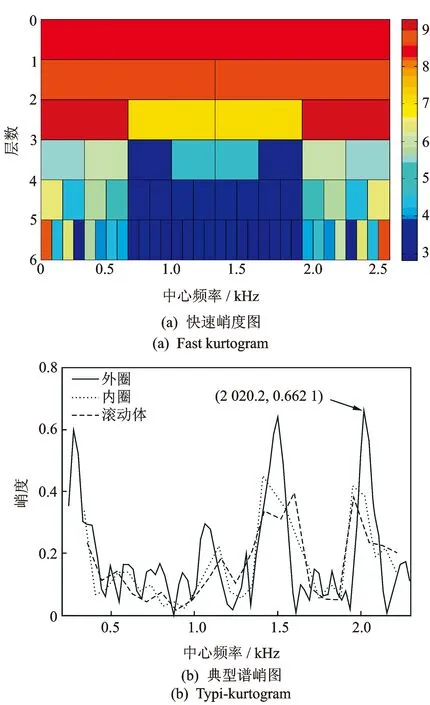
图6 谱峭图比较

从图6(a)中可以得出，快速峭度图中第2层的第1个区间峭度值最大，中心频率为320 Hz，带宽为640 Hz。从图6(b)中可以看出，峭度最大的点为(2 020.2, 0.662 1)，位于外圈典型故障峭度线上。因此，利用典型谱峭图得到最大峭度处的中心频率为2 020.2 Hz，带宽取值为外圈故障特征频率的3倍，即201.9 Hz。

将两种方法得到的中心频率和带宽作为共振解调方法的带通滤波参数，分别进行共振解调分析，得到故障频谱分析图，如图7所示。

从图7(a)中可以看到故障频率为27.0 Hz。受微小划痕影响，图7(a)中除了27.0Hz处的峰值外，存在较多的小尖峰，掩盖了2倍频和3倍频峰值。从图7(b)中可以看到故障频率为29.05 Hz，及其2倍频58 Hz和3倍频87.55 Hz。两种方法分析得到的故障特征频率值与理论计算的滚动体故障特征频率值27.3 Hz都比较相近。由此，可以验证基于典型谱峭图的共振解调方法能够较好地诊断出铁路货车轮对滚动轴承的故障类型。

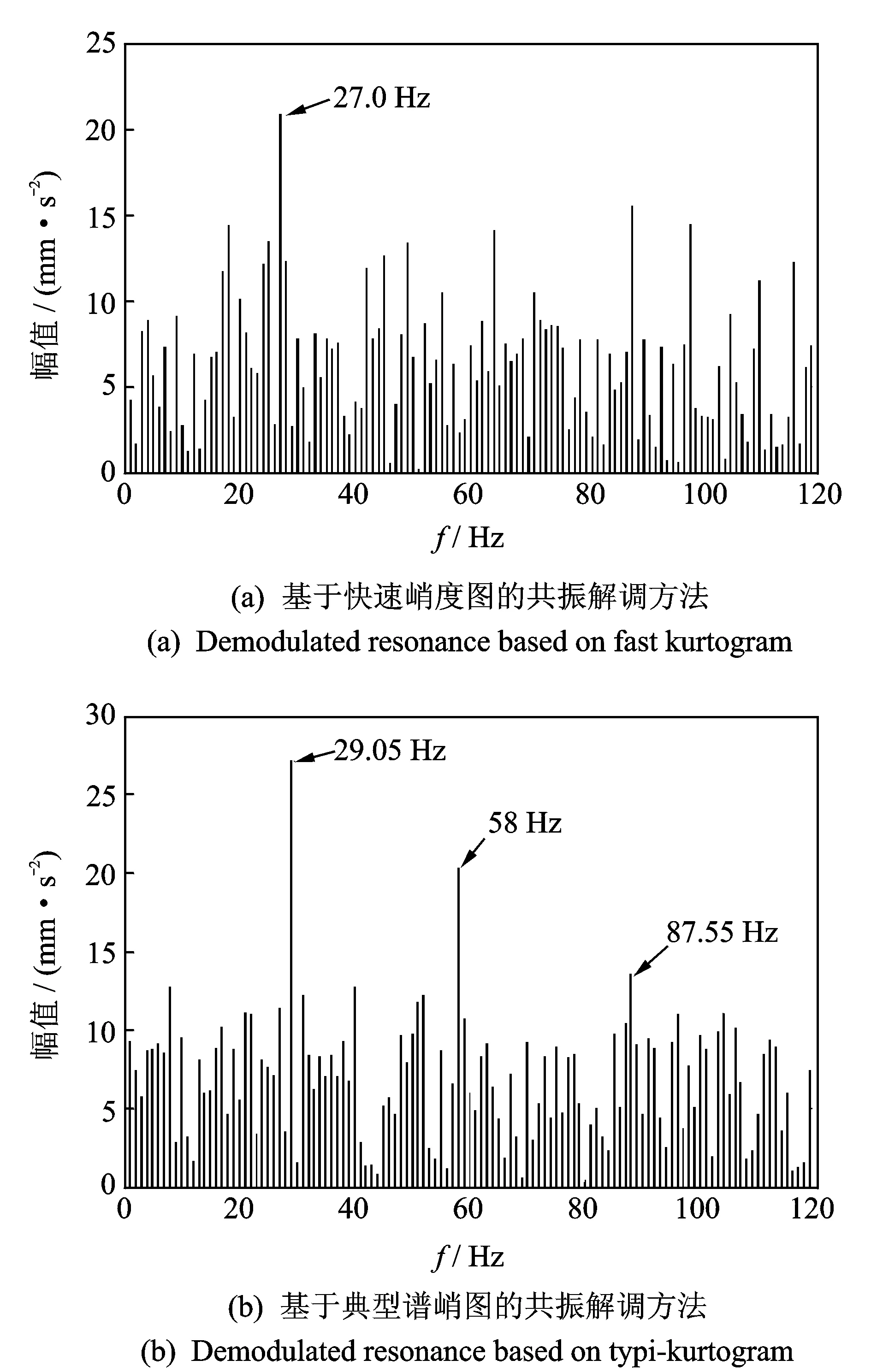
图7 频谱分析比较

基于典型谱峭图的共振解调方法强调工程实际中滚动轴承的典型故障的检测，有较强的针对性。其受到非平稳成分的干扰相对较小，不但能得到典型故障频率，还能得到2倍频和3倍频，能够容易地检测到轴承的滚动体故障。在有先验经验的基础上，相对于基于快速峭度图的共振解调方法自适应较强的优点，基于典型谱峭图的共振解调方法更有利于具体机械环境下滚动轴承典型故障的判别。

4 结束语

笔者在分析了谱峭图方法的基础上，提出了典型谱峭图算法，并与共振解调技术相结合，形成基于典型谱峭图的共振解调方法，用于检测滚动轴承故障。为了验证算法的可行性，在货车滚动轴承实验台上进行故障轴承振动测试。将此方法应用到滚动轴承的故障检测中，能够较好地识别出滚动轴承的故障类型，验证了基于典型谱峭图的共振解调方法的有效性。

[1] 明安波，褚福磊，张炜.滚动轴承故障特征提取的频谱自相关方法[J].机械工程学报，2012,48(19)：65-71.

Ming Anbo, Chu Fulei, Zhang Wei. Feature extracting method in the rolling element bearing fault diagnosis spectrum auto-correlation[J]. Journal of Mechanical Engineering, 2012,48(19):65-71. (in Chinese)

[2] 苏文胜.滚动轴承振动信号处理及特征提取方法研究[D].大连：大连理工大学，2010.

[3] 唐德尧，王定晓，杨政明，等.共振解调技术与机车车辆传动装置故障诊断[J].电力机车技术，2002,25(5)：1-5.

Tang Deyao Wang Dingxiao, Yang Zhengming, et al. Demodulated resonance technique and tailure diagnosing of the gearing on the rolling stock[J]. Technology for Electric Locomotives, 2002,25(5):1-5. (in Chinese)

[4] 周智，朱永生，张优云，等.基于EEMD和共振解调的滚动轴承自适应故障诊断[J]. 振动与冲击，2013,32(2)：76-80.

Zhou Zhi, Zhu Yongsheng, Zhang Youyun, et al. Adaptive fault diagnosis of rolling bearings based on EEMD and demodulated resonance[J]. Journal of Vibration and Shock, 2013,32(2):76-80. (in Chinese)

[5] 张志刚，石晓辉，施全，等.基于改进EMD和谱峭度法滚动轴承故障特征提取[J].振动、测试与诊断，2013,33(3)：478-482.

Zhang Zhigang, Shi Xiaohui, Shi Quan, et al. Fault feature extraction of rolling element bearing based on improved EMD and spectral kurtosis[J]. Journal of Vibration, Measurement & Diagnosis, 2013,33(3)：478-482. (in Chinese)

[6] 彭畅，柏林，谢小亮.基于EEMD、度量因子和快速峭度图的滚动轴承故障诊断方法[J].振动与冲击，2012,31(20)：143-146.

Peng Chang, Bo Lin, Xie Xiaoliang. Fault diagnosis method of rolling element bearings based on EEMD, measure-factor and fast kurtogram[J]. Journal of Vibration and Shock, 2012,31(20)：143-146. (in Chinese)

[7] Barszcz T, Jablonski A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the kurtogram[J]. Mechanical Systems and Signal Processing, 2011,25(1):431-451.

[8] Dwyer R F. Detection of non-gaussian signals by frequency domain kurtosis estimation[C]∥Acoustic, Speech and Signal Processing. Boston: IEEE International Conference on ICASSP, 1983:607-610.

[9] Randall R B, Antoni J. Rolling element bearing diagnostics-a tutorial[J]. Mechanical System and Signal Processing, 2011,25:485-520.

[10]Antoni N J. The spectral kurtosis: a useful tool for characterizing non-stationary signals[J]. Mechanical System and Signal Processing, 2006,20(6):282-307.

[11]Antoni J. Randall R B. The spectral kurtosis: application to the vibration surveillance and diagnostics of rotating machines[J]. Mechanical System and Signal Processing， 2006，20(6)：308-331.

[12]Antoni J. Fast computation of the kurtogram for the detection of transient faults[J]. Mechanical Systems and Signal Processing, 2007,21(1):108-124.

[13]蔡艳平，李艾华，石林锁，等.基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J].振动与冲击，2011,30(2)：167-191.

Cai Yanping, Li Aihua, Shi Linsuo, et al. Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum kurtosis[J]. Journal of Vibration and Shock, 2011,30(2)：167-191. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2015.06.022

*国家自然科学基金资助项目(11372197，11227201)；河北省自然科学基金资助项目(E2014210078)；教育部新世纪优秀人才计划资助项目(NCET-13-0913)

2014-10-09；

2014-12-01

TH133.33; TP391.9

马新娜，女，1978年11月生，副教授。主要研究方向为故障诊断及非线性动力学。曾发表《磁流变阻尼器系统的非线性动力学分析》(《振动与冲击》2011年第30卷第6期)等论文。 E-mail: maxinnamxn@163.com