考虑时变啮合刚度的风机传动链动态性能*

刘 宏，赵荣珍，郑玉巧

(1.兰州理工大学数字制造技术与应用省部共建教育部重点实验室 兰州，730050)(2.兰州理工大学机电工程学院 兰州，730050)



考虑时变啮合刚度的风机传动链动态性能*

刘 宏1,2，赵荣珍1,2，郑玉巧1,2

(1.兰州理工大学数字制造技术与应用省部共建教育部重点实验室 兰州，730050)(2.兰州理工大学机电工程学院 兰州，730050)

针对大型风力发电机组齿轮传动链动态刚度引起的机组结构振动问题，综合轮齿弯曲变形、齿根过度圆角处的基体变形和接触变形等因素，建立齿轮时变啮合刚度的量化分析模型，并与有限元动态啮合模型对比验证理论模型的正确性。在此基础上考虑齿轮时变啮合刚度和轴扭转刚度推导1.5 MW风力机传动链的动态总刚度，用于分析传动链在动态刚度下固有特性变化规律及传动链临界转速对动态刚度参数的敏感性，量化显示动态刚度幅值变化引起的临界转速波动。研究表明,齿轮时变啮合刚度的波动会引起传动链临界转速的不稳定，增大时变刚度幅值会引起转子系统临界转速的升高，但总体上啮合刚度波动对临界转速的影响处于非敏感区。本研究对揭示风力机齿轮传动链的内部刚度激励机理和实现系统动态性能优化设计提供理论依据。

风力发电机； 传动链； 啮合刚度； 临界转速； 参数敏感性

引 言

增速箱是风力机组的关键部件之一，常工作于重载、冲击和变载荷等复杂工况下，且机组高空架设、维修较困难等问题对其可靠性提出了更高的要求[1]。传动齿轮对的啮合刚度是传动链内部重要的激励源，掌握其运行机理对于研究传动链动力学特性和可靠性设计极其重要，因而围绕齿轮啮合刚度的风力机传动链动力学分析和设计的研究受到了广泛关注[2-3]。

目前，国内外针对风力发电机齿轮传动链的研究尚处于起步阶段[4]，相关研究主要是将齿轮啮合刚度简化为定值模型展开，而传动链的动态响应受齿轮时变啮合刚度的影响[5]，特别在高速重载情况下更为明显。因此，为保证分析的精确性需要考虑时变啮合刚度的传动链模型。在这一问题的研究中有限元方法[6-7]应用较为广泛，但该方法需要模型网格细化工作并占用较多的计算时间，且风力机齿轮传动链结构复杂，内部啮合齿轮对较多，难于细化模型。影响振动的因素，特别是振动与其他运行参数之间关系非常复杂。然而，大型风力发电机组通过实测的方法难度大、成本高，基于理论分析的方法考虑齿轮时变啮合刚度建立风力机传动链行星轮系部分的动力学模型[8]，通过仿真计算，能够获得齿轮动态啮合力，为时变啮合刚度的理论验证提供新的思路。同时，一些学者将时变啮合刚度计入传动链模型中，分析系统的动态响应特性[9-10]和齿轮传动链的振动水平，探讨传动链的优化设计方法，加深了对风力机传动链的认识。

基于上述情况，本研究以风力机传动链中单对啮合齿轮为研究对象，对建立齿轮时变啮合刚度的量化分析模型问题进行研究，采用有限元动态啮合模型对比验证，在此基础上细化增速齿轮箱，推导1.5 MW风力机齿轮传动链的动态总刚度，量化分析传动链在动态刚度下的固有特性及传动链临界转速对动态刚度参数的敏感性。

1 轮齿啮合刚度的量化分析模型

1.1 弯曲变形

齿轮啮合刚度反映了齿轮接触过程中接触齿轮对数目的周期性变化及其啮合线从齿根到齿顶的不均匀变化过程。它是一个周期性变化量，包括齿形的几何特征、接触点位置、轮齿挠度及齿形误差等多方面因素。依据轮齿的弯曲、齿根过度圆角处的基体变形和接触变形计算单齿的刚度和齿轮对的啮合刚度。本研究将轮齿看作如图1所示的不均匀悬臂梁，齿根部分悬臂固定在基体上，梁的有效长度为Le，沿啮合线方向将轮齿划分为n个微段，取其中一微段ei，假设啮合齿轮对之间的啮合力为F，由啮合原理可知，F的大小和方向随着啮合点的移动而变化。以δb表示轮齿的弯曲变形，则轮齿的弯曲变形可表示为各微段变形的总和[11]

(1)

其中：α为压力角；G为材料剪切模量。

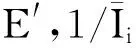
(2)

(3)

其中：Ii为极惯性矩；Ai为轮齿接触段面积；E为弹性模量；ν为泊松比。

由梁的弯曲刚度的计算方法可计算轮齿的弯曲刚度，表示为

kb=F/δb

(5)

图1 轮齿啮合模型

1.2 齿根过渡圆角处的基体变形

根据Muskshelishvili理论在弹性圆环中的应用，假设齿根圆部分受到恒定的随时间变化的作用力，则该变形量δf[12]为

(6)

其中：W为齿宽。

L*，M*，P*和Q*可利用多项式函数式求得

(7)

其中：sf为单齿齿根对应齿轮基体的弧长；θf为sf/2所对应的齿轮圆心角；hfi为齿根圆半径与基体内孔半径的比值；系数Ai，Bi，Ci，Di，Ei和Fi的取值见表1[12]。

齿根过度圆角处的刚度系数kf可表示为

kf=F/δf

(8)

表1 多项式函数系数取值

Tab.1 The coefficient of polynomial function

系数L*M*P*Q*Ai×10-5-5.574060.111050.9520-6.2042Bi×10-3-1.9986-1.9986185.50009.0089Ci×10-4-2.3015-83.43100.05384.0964Di×10-34.7702-9.92560.05384.0964Ei0.02710.16240.2895-0.1472Fi6.80450.90860.92360.6904

1.3 接触变形

根据已有文献的研究结论，接触齿轮对的赫兹接触刚度可近似表达为式(9)所示的常数kh[13]。其数值大小与接触线位置和渗透深度无关，仅由齿宽和齿轮材料的力学性能决定

kh=πEW/4(1-ν2)

(9)

1.4 齿轮对的啮合刚度计算方法

综合单齿弯曲变形、齿根过度圆角处基体变形和接触变形，啮合齿轮对的啮合刚度ksp可表示为

ksp=1/(1/kbs+1/kbp+1/kfp+1/kfs+1/kh)

(10)

其中：kbs和kbp分别为太阳轮和行星轮的单齿弯曲刚度；kfp和kfs分别为太阳轮和行星轮齿根过度圆角处基体变形刚度。

2 时变啮合刚度的计算方法设计

2.1 方法设计

一对齿轮啮合传动的区间是有限的，为了能够连续传动，必须保证在前一轮齿尚未脱离啮合时，后一对轮齿能及时进入啮合。单齿和双齿啮合的周期性变化引起齿轮啮合刚度的周期性波动，从而造成了系统内部振动和噪声，其啮合区域的变化如图2所示。从齿轮啮合原理的角度，分析影响轮齿啮合刚度变化的因素，主要由以下方面造成：a．在单齿啮合周期内同等啮合力作用下，因轮齿截面的不均匀性，使得轮廓齿面各点位移不同；b．整个齿轮啮合过程中，单双齿啮合周期性变化使得轮齿位移和啮合作用力也是变化的。

以传动链中行星轮系传动建立轮齿啮合模型，主轴将动力传递给行星架，由行星架带动3个行星轮驱动中心的太阳轮，假设太阳轮的运行速度为n1，且有Z1个齿，行星轮齿数为Z2，则单个齿的啮合周期Te=60/n1Z1。该对啮合齿轮的重合度εα为

εα=[Z1(tanαa1-tanα′)+Z2(tanαa2-tanα′)]/2π

(11)

其中：α′为啮合角；αa1和αa2分别为齿轮1和2的齿顶圆压力角。

图2中Lc为单齿啮合周期，根据太阳轮和行星轮参数计算得齿轮啮合重合度。将轮齿接触区域划分为3段，在接触的起始端(a端)有2对轮齿接触啮合(a～c段)，然后1对轮齿退出啮合(c～e段)，随下一对轮齿相继啮合，进入双齿啮合区域(e～g段)。考虑整个齿轮连续传动重合度εα，实际动力学方程中需要的是齿轮综合时变啮合刚度，因此整个齿轮的时变内核刚度是有多对轮齿刚度综合而成，对齿啮合刚度在啮合周期内叠加获得整个齿轮的啮合刚度。

图2 轮齿接触区域

2.2 应用验证情况

以1.5 MW风力机齿轮箱内太阳轮及与之啮合的行星轮为研究对象，其具体参数见表2。计算得太阳轮和行星轮啮合重合度εα=1.51，双齿啮合区域占总啮合区域的33.8%，单齿啮合区域占总啮合区域的32.4%。

表2 齿轮参数

在机组额定风速工作条件下由主轴输入到太阳轮的扭矩为179.4 Nm，将扭矩向啮合齿面转化，假设3个行星轮承受相同的载荷条件，则施加到每个行星轮轮齿上的力为1.2 kN，由式(5),(7),(8)和(9)借助Matlab计算1对轮齿从进入啮合到脱离啮合1个周期内的刚度值，计算结果如图3所示。

图3 单齿啮合刚度

从图3可知，轮齿啮合刚度的大小与啮合位置密切相关。从齿根到齿顶啮合的过程中，靠近齿根部分区域啮合刚度迅速减小，越过齿轮分度圆后又缓慢增大，但齿顶附近的最大值小于齿根部分啮合刚度的最大值。通过单对齿啮合刚度在啮合周期内叠加获得整个齿轮的啮合刚度曲线见图4。

图4 齿轮时变啮合刚度

从图4可知，时变啮合刚度是一个周期性变化的量，其变化周期不再是单齿啮合周期Lc，而是被重合度εα重新划分为(2-εα)Lc。整个周期内有两种变化趋势，且单、双齿变化之间为突变过程，啮合刚度的最大值出现在双齿啮合区，最小值出现在单齿啮合区。

3 轮齿啮合刚度的有限元模型构造

采用三维实体建立行星轮系齿轮啮合有限元模型，由于在有限元齿轮静态接触模型中，对两个啮合齿轮施加了全约束，实体单元没有旋转自由度，不能反映啮合齿面上各点随啮合运动的位移变量。结合齿轮的工作要求，建立齿轮动态啮合模型，该模型结合Ansys的参数化设计语言APDL建立，包括完整的齿轮结构。约束控制节点3个方向的平动自由度，保证齿轮的啮合运动，向主动轮施加扭矩。为获得一个齿啮合范围内啮合齿面沿啮合线方向各点的位移和啮合力大小，在齿面啮合线方向上均匀取10个节点作为1个节点集，将这些节点位移定义为变量，从而获取各啮合节点在单齿啮合周期内沿x和y两个方向的变化量δx和δy，则总位移为

δ=δxcosα+δysinα

(12)

节点集的变形计算结果如图5所示，则单齿啮合刚度计算如下

k=F/δ

(13)

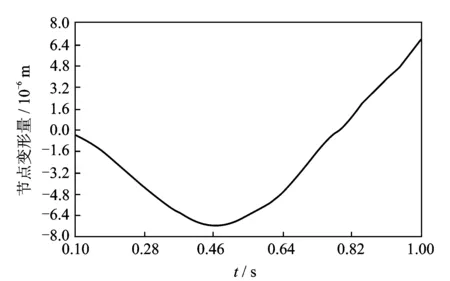
图5 啮合齿面节点位移

图6给出了采用理论分析模型和有限元仿真模型两种方法求解得到的单齿动态啮合刚度结果曲线。对比分析显示，有限元动态啮合模型在Ansys软件中所模拟的单齿啮合刚度值与理论计算的啮合刚度值在轮齿进入啮合和脱离啮合的很小区间内误差较大，其余啮合区间上刚度值基本相同，且具有相同的变化趋势，证明了理论分析模型在计算单对齿轮啮合刚度上的有效性。

图6 啮合刚度对比分析

4 考虑时变啮合刚度的风力机传动链动态响应

4.1 传动链动力学建模

将动刚度模型应用于1.5MW水平轴风力机传动链(包括1级行星级和2级平行级齿轮传动)中，行星级动力由行星架输入，太阳轮输出，内齿圈固定的结构形式，并用3个行星轮承担载荷。其动力学模型如图7所示。

图7 传动链动力学模型

模型中齿轮和轴假设成刚体，根据有关研究结论，齿轮啮合振动的轴向、径向振动中，轴向扭转振动最为重要[12]。因此，只考虑系统的扭转振动，应用拉格朗日方法建立系统的动力学方程

(14)

其中：q={qcqpqsq4q5q6q7}T为广义坐标表示各自由度处的位移；F为外部力矢量；J为系统质量矩阵，J=diag[Jc3Jp+3mdJsJ4J5J6J7]；K(t)为由系统齿轮啮合刚度和轴扭转刚度组成的时变矩阵。

(15)

其中：ki(t)为齿轮时变啮合刚度；kj为轴扭转刚度(i=c,p,4,6;j=s,5)。

系统的刚度矩阵是一个时变矩阵，可表示为一个常数矩阵(平均值)k1和一个动态矩阵(波动矩阵)k1(t)的线性叠加，即

K(t)=k1+k1(t)

(16)

工程上，一般在讨论结构固有特性时不计阻尼作用，由运动方程考虑系数矩阵k1可求得其无阻尼特征值，于是式(14)可变为

(17)

其中：φi为系统的阵型矩阵；ωi为系统自由振动的圆频率。

按照机组系统的设计参数，齿轮动态啮合刚度按前述方法依次进行参数化建模获取，计算系统的固有频率见表3。

表3 系统固有频率

4.2 传动链临界转速分析

传动链两级平行轴部分转速不一致，为分析方便，把系统各部分向行星轮系输出轴当量化处理，以太阳轮轴为等效构件，将平行轴的力和位移均用等效构件上的等效量来代替，当量化前后保证系统的动能和势能守恒。将齿轮看成圆盘，圆盘间用啮合刚度相连，传动轴以扭转刚度替代，再将各圆盘视为支点的回转圆盘，通过传动轴传递转动和扭矩，则系统成为单轴系统。由于风载荷的随机性，将风轮的发电转速(11 ～ 22 r/min)折算到高速轴上，在Ansys中建立不同角速度下转子的多载荷步模态分析模型，并计算得到系统的转速频率分布图，如图8所示。

由坎贝尔图解得到转子系统的1阶临界转速为2 735.04 r/min，2阶为3 958.9 r/min，3阶为7 306.7 r/min，4阶为10 530.6 r/min。额定工况下系统的额定转速为1 500 r/min，计算可得工作转速偏离其临界转速的裕度为82%，工作转速相对于临界转速的裕度远大于30%，因此裕度较大，满足工作转速偏离临界转速裕度的规定[14]。

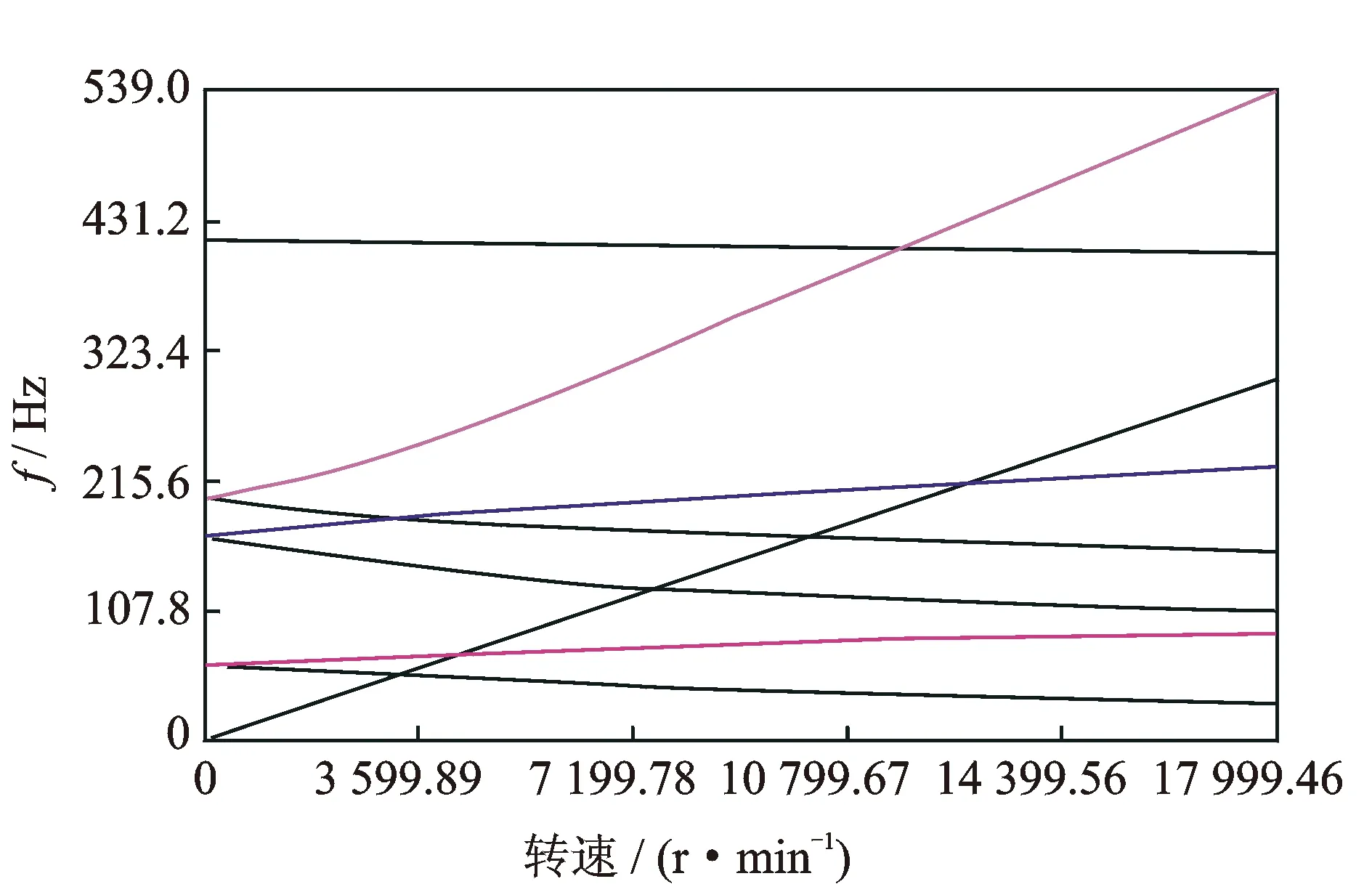
图8 传动链转速-频率分布图

4.3 参数敏感性分析

为了进一步研究齿轮时变啮合刚度与传动链的耦合作用，进行齿轮时变啮合刚度参数对系统临界转速敏感性分析。考虑时变啮合刚度从平均值7.74×108N/mm增大至动刚度的最大值9.86×108N/mm(增大21.5%)时，再次对系统分析模型进行求解，将变化前后所得系统临界转速进行对比，分析参数敏感性，如表4所示。

表4 转子临界转速对比

对比分析发现，啮合刚度的变化对系统临界转速的影响并不明显，随着啮合刚度波动值提高21.5%，达到波动的最大值时，系统1阶临界转速增大4.1%，即啮合刚度稍有变化不会引起临界转速的很大变化，故表现出对该参数的不敏感。因此，系统有相对确定的临界转速，有利于系统工作频率避开固有频率而稳定地工作。

5 结 论

1) 将轮齿视为悬臂梁，综合轮齿弯曲变形、齿根过度圆角处的变形和接触变形建立了齿轮时变啮合刚度的量化分析模型，并采用Ansys参数化设计语言APDL建立动态啮合模型进行验证，对比显示两种方法的计算结果，验证了时变啮合刚度理论建模方法的可行性。

2) 基于此，建立了1.5 MW水平轴齿轮传动链的动力学模型，获取了传动链动态总刚度矩阵，1阶临界转速为2 735.04 r/min，工作转速相对于临界转速有充分的裕度。

3) 通过绘制不同啮合刚度下转子系统的坎贝尔图，分析了系统临界转速与啮合刚度之间的量化关系，结果显示时变啮合刚度的波动会引起系统临界转速变化，但总体上呈现系统临界转速对动态刚度不敏感。

[1] 陈涛,孙伟,张旭.基于灰色关联度的风电齿轮箱传动系统故障树分析[J].太阳能学报,2012,33(10):1655-1660.

Chen Tao, Sun Wei, Zhang Xu. Reliability analysis of gearbox transmission for wind turbine based on fault tree model [J]. Acta Energiae Solaris Sinica, 2012,33(10):1655-1660. (in Chinese)

[2] 张义民,何永慧,朱丽莎,等.多平行轴齿轮耦合转子系统的振动响应[J].振动、测试与诊断,2012,32(4):527-531.

Zhang Yimin, He Yonghui, Zhu Lisha, et al. Vibration response of multi-shaft rotor system with coupled gear mesh[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(4):527-531. (in Chinese)

[3] 苏春,周小荃.基于有效年龄的风力机多部件维修优化[J].东南大学学报,2012,42(6):1100-1104.

Su Chun, Zhou Xiaoquan. Maintenance optimization for multi-component of wind turbine based on effective age[J]. Journal of Southeast University, 2012,42(6):1100-1104. (in Chinese)

[4] Peeters J L M, Vandepitte D, Sas P. Analysis of internal drive train dynamics in a wind turbine[J]. Wind Energy, 2006,9(1):141-161.

[5] Helsen J, Vanhollebeke F, Deconinck F, et al. Insights in wind turbine drive train dynamics gathered by validating advanced models on a newly developed 13.2MW dynamically controlled test-rig[J]. Mechatronics, 2011,21(4):737-752.

[6] 朱丽莎,张义民,马辉,等.直齿轮耦合转子系统的振动可靠性研究[J].振动、测试与诊断,2013,33(2):258-262.

Zhu Lisha, Zhang Yimin, Ma Hui, et al. Iterative learning control on double-valve parallel electro-hydraulic servo force control system [J]. Journal of Vibration, Measurement & Diagnosis,2013,33(2):258-262. (in Chinese)

[7] 于印鑫,袁惠群,梁明轩,等.基于显式动力学的某齿轮轴冲击应力分析[J].振动、测试与诊断,2013,33(2):273-276.

Yu Yinxin, Yuan Huiqun, Liang Mingxuan, et al. Impact stress analysis of gear shaft based on explicit dynamic[J]. Journal of Vibration, Measurement & Diagnosi, 2013,33(2):273-276. (in Chinese)

[8] 秦大同,周志刚,杨军,等.随机风载作用下风力发电机齿轮传动系统动态可靠性分析[J].机械工程学报,2012,48(3):1-8.

Qin Datong, Zhou Zhigang, Yang Jun, et al. Time-dependent reliability analysis of gear transmission system of wind turbine under stochastic wind load[J]. Journal of Mechanical Engineering, 2012,48(3):1-8. (in Chinese)

[9] 张庆伟, 张博,王建宏,等.风力发电机齿轮传动系统的动态优化设计[J].重庆大学学报,2010,33(3):30-35.

Zhang Qingwei, Zhang Bo, Wang Jianhong, et al. Dynamic optimization design of gear transmission system for wind turbine[J]. Journal of Chongqing University, 2010,33(3):30-35. (in Chinese)

[10]Maki K, Sbragio R, Vlahopoulos N. System design of a wind turbine using a multi-level optimization approach[J]. Renewable Energy, 2012,43:101-110.

[11]Chaari F, Baccar W, Abbes M S, et al. Effect of spalling or tooth breakage on gearmesh stiffness and dynamic response of a one-stage spur gear transmission[J]. European Journal of Mechanics, 2008,27(4):691-705.

[12]Sainsot P, Velex P, Duverger O. Contribution of gear body to tooth deflections-a new bidimensional analytical formula[J]. Journal of Mechanisms, 2004,126(4):748-752.

[13]Yang D C H, Sun Z S. A rotary model for spur gear dynamics[J]. Journal of Mechanisms Design, 1985,107(4):529-535.

[14]付才高.转子动力学及整机振动[M]. 北京:航空工业出版社,2000:67-68.

10.16450/j.cnki.issn.1004-6801.2015.06.004

*国家自然科学基金资助项目(51165019)；甘肃省自然科学基金资助项目(1308RJYA018)

2013-11-16；

2014-03-03

TH132.413; TH113.1

刘宏,男，1986年4月生，博士研究生。主要研究方向为风力发电机机械系统动力学、多体系统动力学分析。 E-mail：hongliu2006@163．com